
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приемы разработки и выбора управленческих решений в условиях неопределенностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Сущность неопределенности и риска. Принимаемые управленческие решения всегда спроектированы в будущее, поэтому ЛПР в момент принятия решения часто не может с абсолютной уверенностью знать, как будут развиваться события, как будет изменяться ситуация. Иными словами, в момент принятия управленческого решения значителен элемент неопределенности и риска. Риск — это возможная опасность потерь, вытекающая из специфики тех или иных явлений природы и видов деятельности человеческого общества. Это историческая и экономическая категория. Таким образом, принятие решений в условиях риска означает выбор варианта решения в условиях, когда каждое действие приводит к одному из множества возможных частных исходов, причем каждый исход имеет вычисляемую или экспертно определяемую вероятность появления. Как историческая категория риск представляет собой осознанную человеком возможную опасность. Это свидетельствует о том, что риск исторически связан со всем ходом общественного развития. Как экономическая категория риск представляет собой событие, которое может произойти или не произойти. Неопределенность — это неполнота или недостоверность информации об условиях реализации решения, наличие фактора случайности или противодействия. Таким образом, принятие решения в условиях неопределенности означает выбор варианта решения, когда одно или несколько действий имеют своим следствием множество частных исходов, но их вероятности совершенно не известны или не имеют смысла. Неопределенность хозяйственной ситуации обусловливается следующими факторами: отсутствием полной информации, случайностью, противодействием. Отсутствие полной информации о хозяйственной ситуации и перспектив ее изменения заставляет предпринимателя искать возможность приобрести недостающую дополнительную информацию, а при отсутствии такой возможности начать действовать наугад, опираясь на свой опыт и интуицию. Случайность во многом определяет неопределенность хозяйственной ситуации. Случайность — это то, что в сходных условиях происходит неодинаково, и поэтому ее заранее нельзя предвидеть и спрогнозировать. Однако при большом количестве наблюдений за случайностями можно обнаружить, что в мире случайностей действуют определенные закономерности. Математический аппарат для изучения этих закономерностей дает теория вероятности. Случайные события становятся предметом теории вероятности только тогда, когда с ними связываются определенные числовые характеристики — их вероятности. Противодействие также во многом определяет неопределенность хозяйственной ситуации. На любое действие всегда имеется противодействие. К противодействиям относятся катастрофа, пожар и другие природные явления, война, революция, забастовка, различные конфликты в трудовых коллективах, конкуренция, нарушения договорных обязательств, изменение спроса, аварии, кражи и т.п. Предприниматель в процессе своих действий должен выбрать такую стратегию, которая позволит ему уменьшить степень противодействия, что, в свою очередь, снизит и степень риска. Применение теории игр в практике управления. Теория игр все шире проникает в практику экономических решений и исследований. Ее можно рассматривать как инструмент, помогающий повысить эффективность плановых и управленческих решений. Обычно теорию игр определяют как раздел математики для изучения конфликтных ситуаций. Это значит, что можно выработать оптимальные правила поведения каждой стороны, участвующей в решении конфликтной ситуации. В экономике аппарат математического анализа, занимающийся определением экстремумов функций, оказался недостаточным. Появилась необходимость изучения так называемых оптимальных минимаксных и максиминных решений. Таким образом, теорию игр можно рассматривать как новый раздел оптимизационного подхода, позволяющего решать новые задачи при принятии решений. Математический аппарат для выбора стратегии в конфликтных ситуациях дает теория игр. Она позволяет предпринимателю или менеджеру лучше понимать конкурентную обстановку и свести к минимуму степень риска. Анализ с помощью приемов теории игр побуждает предпринимателя (менеджера) рассматривать все возможные альтернативы как своих действий, так и стратегии партнеров, конкурентов. Формализация данного процесса позволяет улучшить понимание проблем в целом. Таким образом, теория игр — собственно наука о риске. Теория игр позволяет решать многие экономические проблемы, связанные с выбором, определением наилучшего положения, подчиненного только некоторым ограничениям, вытекающим из условий самой проблемы. Основные понятия теории игр. В теории используются следующие понятия: – игра — упрощенная формализованная модель реальной конфликтной ситуации. Математически формализация означает, что выработаны определенные правила действия сторон в процессе игры: варианты действия сторон; исход игры приданном варианте действия; объем информации каждой стороны о поведении всех других сторон. Одну играющую сторону при исследовании операций может представлять коллектив, преследующий некоторую общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценивать количественно; – игрок — одна из сторон в игровой ситуации; – стратегия игрока — правила действия игрока в каждой из возможных ситуаций игры. Существуют игровые системы управления — системы, процесс управления в которых рассматривается как игра; – платежная матрица — матрица эффективности, матрица игры. Она включает все значения выигрышей (в конечной игре). Пусть игрок 1 имеет т стратегий Аi, а игрок 2 — n стратегий Вj(i=1,т; j=1,n). Игра может быть названа игрой т х п. Представим матрицу эффективности игры двух лиц с нулевой суммой, сопроводив ее необходимыми обозначениями (таблица 1). Таблица 1 Платежная матрица
В данной матрице элементы аij (значения выигрышей игрока) могут означать и математическое ожидание выигрыша (среднее значение), если выигрыш — случайная величина. Величины αi, i=1,т - минимальные (максимальные) значения элементов аij по строкам и βj, j=1,n — максимальные — по столбцам.
При разработке и принятии управленческого решения в условиях неопределенности всегда неизбежен элемент риска, наличие которого проистекает из исходной неопределенности информации о состоянии среды, в которой предстоит реализация решения. Теория игр и статистических решений содержит достаточный арсенал методов, позволяющих принимать решения в условиях неопределенности. В условиях, когда отсутствуют данные о вероятности, но существует отдаленная возможность оценки результатов действий, также используются специальные приемы: 1. Критерий математического ожидания. 2. Критерий Лапласа — «ориентируйся на среднее». 3. Критерий Вальда (наибольшая осторожность или крайний пессимизм) — «рассчитывай на худшее». 4. Критерий Сэвиджа (минимизация большого риска) — «рассчитывай на лучшее». 5. Критерий крайнего оптимизма — «верь в удачу» (максимакс). 6. Критерий Гурвица — «компромисс, или критерий пессимизма-оптимизма». При реализации данных приемов предполагается, что принятие и реализация управленческих решений проводятся в условиях разного состояния среды Sj, количество которых можно подсчитать, — количество Sj конечно и равно п. Все возможные состояния известны, неизвестно только, какое состояние будет иметь место в условиях, когда планируется реализация принимаемого управленческого решения. Будем также считать, что множество управленческих решений (стратегий) Ri также конечно и равно т. Допустим, каждому управленческому решению Ri и каждому возможному состоянию среды Sj соответствует результат (исход) Vij,определяющий результат (выигрыш, полезность) при принятии (выборе) j- го решения и реализации i- го состояния. В ряде случаев в качестве результатов рассматривается матрица рисков || rij ||.
Содержание и особенности использования указанных критериев. 1. Критерий математического ожидания является первичным при использовании приемов принятия решений в условиях неопределенности и риска. Он предназначен для выбора оптимальной стратегии поведения, т.е. пригоден для принятия серии решений. Математическое ожидание является средним значением случайной величины и может быть рассчитано по формуле:
где Pij – вероятность реализации i – го варианта j – й ситуации.
2. Критерий Лапласа – «ориентируйся на среднее». Применяется тогда, когда равновероятны все состояния среды.
3. Критерий Вальда (критерий максимина, крайнего пессимизма) - «рассчитывай на худшее». Оптимальной будет стратегия, ориентированная на получение максимального из минимальных выигрышей.
Этот критерий ориентирует ЛПР на наихудшие условия и рекомендует выбрать ту стратегию, для которой выигрыш максимален.
4. Критерий Сэвиджа (критерий минимакса, минимизации большого риска) — «рассчитывай на лучшее». Принимается стратегия, содержащая риск, который при различных вариантах обстоятельств окажется минимальным.
где Критерий Сэвиджа, как и критерий Вальда, - это критерий крайнего пессимизма, но пессимизм проявляется в том, что минимизируется максимальная потеря в выигрыше по сравнению с тем, чего можно было бы достичь в данных условиях.
5. Критерий крайнего оптимизма (критерий максимакса)— «верь в удачу».
Максимаксный критерий предполагает, что состояние среды будет наиболее благополучным, поэтому необходимо выбрать решение, обеспечивающее максимальный выигрыш среди максимально возможных.
6. Критерий Гурвица (критерий компромисса, или критерий пессимизма-оптимизма».
где НА -критерий пессимизма-оптимизма применительно к матрице А, р -коэффициент пессимизма (оптимизма), выбираемый экспертно из интервала между 0 и1 (0 ≤ р ≤). Согласно этому критерию при выборе решения в условиях неопределенности не руководствоваться ни крайним пессимизмом (всегда рассчитывать на худшее), ни оптимизмом (все будет наилучшим образом). Рекомендуется некое среднее решение. Использование коэффициента р вносит дополнительный субъективизм в принятие решений.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

 ,
,
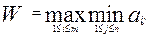
 ,
, , где
, где  , при заданном j.
, при заданном j.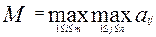
 ,
,


