
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрон в атоме водорода в основном состоянии.Содержание книги
Поиск на нашем сайте
В этом случае используются сферические координаты: радиус-вектор r и угловые координаты j и q (см.рис.). Чтобы представить сложность решения, мы приведем вид оператора Лапласа в сферических координатах:
В общем случае пси-функция зависит от трех координат: Y = Y (r, q, j). При использовании сферических координат пси-функцию можно представить в виде трех сомножителей, каждый из которых зависит только от одной координаты:
R, Q и F, т.е. разделим переменные. Нижние индексы показывают, какие квантовые числа (см. дальше) появляются в решениях для этих функций. Мы будем рассматривать только радиальную часть оператора Лапласа, иначе говоря, случай, когда атом водорода находится в основном состоянии. Функция R называется радиальной частью пси-функции.
При решении нам нужно определить: полную энергию Е электрона и неизвестные величины С и а. Найдем производные R¢ и R ², подставим их и R в уравнение Шрёдингера.
После сокращений получим уравнение (·), в котором 2-й и 4-й члены содержат r, а два других - нет. Т.к. это уравнение должно выполняться при любых r, в том числе при r = 0, то из (·) мы получим два уравнения, из которых найдем а и Е.
Коэффициент С найдем из условия нормировки.
В результате получим:
Введем понятие радиальной плотности вероятности. Плотность вероятности в нашем случае – это ç R ç2 – по определению равна
Из рисунка видно, что максимальная вероятность обнаружить электрон при наименьшей его энергии совпадает с 1-ым боровским радиусом а. Энергия электрона в атоме водорода квантуется, выражение для нее получается такое же, как в теории Бора, но из приведенного выше решения это не следует, т.к. мы рассматривали только основное состояние.
КВАНТОВЫЕ ЧИСЛА При решении уравнения Шрёдингера автоматически (т.е. без каких либо искусственных предположений) появляются целые числа, которые называются квантовыми числами. Таких чисел три: n, l и m. Впоследствии из релятивистского уравнения Дирака следовало и четвертое квантовое число ms. Каждое из квантовых чисел входит в выражение какой-либо физической величины и свидетельствует о том, что данная величина квантуется, т.е. может принимать дискретные значения. Состояние электрона в квантовой системе полностью описывается с помощью 4-х квантовых чисел: n, l, m, ms.
Таким образом, из квантовой механики следует, что энергия электрона, его орбитальные моменты, проекции орбитальных моментов на внешнее поле - квантуются. Они не могут иметь любые значения, а только те, которые определяются приведенными выше соотношениями. Собственный момент электрона имеет только одно значение, а его проекция на внешнее поле – два значения ±
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.192.248 (0.009 с.) |


 радиальная часть
оператора
радиальная часть
оператора

 Если подставить Y в уравнение Шрёдингера, то получим три уравнения для
Если подставить Y в уравнение Шрёдингера, то получим три уравнения для




 (·)
(·)





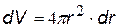 (на рис.- заштрихован)
(на рис.- заштрихован)










 Отношение орбитальных магнитного и механического моментов
Как векторы они направлены противоположно
Отношение орбитальных магнитного и механического моментов
Как векторы они направлены противоположно



 – см.рис.
– см.рис.





 ms - магнитное собственное квантовое число;
Входит в выражение для проекций собственного механического Lсобст и магнитного рсобст моментов на направление Z внешнего поля (например, магнитного). Показывает, что ориентация Lсобств. (спина – см. дальше) может иметь только два значения.
ms - магнитное собственное квантовое число;
Входит в выражение для проекций собственного механического Lсобст и магнитного рсобст моментов на направление Z внешнего поля (например, магнитного). Показывает, что ориентация Lсобств. (спина – см. дальше) может иметь только два значения.




 , связанный с некоторым движением («вращением») электрона вокруг собственной оси (см.рис.)
, связанный с некоторым движением («вращением») электрона вокруг собственной оси (см.рис.)



 Чтобы представить сложность поведения электрона даже в простейшем атоме Н, на рисунке представлена плотность вероятности для электрона в состоянии с n = 4, l = 2, m = ± 1. Светлые пятна - это области, в которых наиболее вероятно пребывание электрона. Это только плоский срез, в действительности вероятность имеет объемное распределение.
Чтобы представить сложность поведения электрона даже в простейшем атоме Н, на рисунке представлена плотность вероятности для электрона в состоянии с n = 4, l = 2, m = ± 1. Светлые пятна - это области, в которых наиболее вероятно пребывание электрона. Это только плоский срез, в действительности вероятность имеет объемное распределение.


