
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновая функция, ее статистический смысл. Соотношение неопределенностей Гейзенберга.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Природа волн де Бройля. Впервые квантовые свойства были открыты у электромагнитного поля (1900). Волны де Бройля связаны с любой движущейся микрочастицей и имеют специфическую квантовую природу. Групповая скорость волн де Бройля u = dω dk =υ равна скорости частицы. Фазовая скорость волн де Бройля определяется как Соотношение неопределенностей Гейзенберга. Один из фундаментальных результатов квантовой механики – выявление факта существования пар физических величин, описывающих движение одной частицы, которые не могут одновременно иметь точные значения. Их называют сопряженными величинами. Реальное поведение микрочастиц показывает, что Ǝ предел точности, с которой динамические переменные (координаты, импульс, момент импульса, энергия и др.) могут быть указаны и измерены. Этот предел не зависит от степени совершенства измерительного прибора. Он обусловлен 2 факторами: корпускулярно-волновым дуализмом и взаимодействием наблюдаемого объекта с регистрирующим прибором. Квантовая механика утверждает, что положение и скорость микробъекта одновременно не могут быть точно известны. Эта идея составляет суть принципа неопределенности (в 1927 г. немецким физиком В. Гейзенбергом). Количественные соотношения, выражающие этот принцип в конкретных случаях, называют соотношениями неопределенностей. Рассмотрим 2 наиболее важных соотношения неопределенностей. Сформулируем соотношение неопределенностей, ограничивающее точность одновременного измерения координат и соответствующих проекций импульса частицы. Если ∆x – неопределенность значения координаты х центра масс системы, а ∆px – неопределенность проекции импульса pr на ось Х, то произведение этих неопределенностей должно быть не меньше постоянной Планка h. Аналогичные неравенства должны выполняться для координат y и z и проекций импульса py и pz соответственно: (1)
Соотношение неопределенностей, устанавливающее неопределенность измерения энергии ∆E за данный промежуток времени ∆t, имеет вид Поясним смысл этих соотношений. Первое из них утверждает, что если положение частицы, например, по оси X известно с неопределенностью ∆x, то в тот же момент времени проекцию импульса частицы на эту же ось можно измерить только с неопределенностью ∆px, не меньшей чем h (2∆x.) Чем точнее х, тем менее точно можно установить рх, и наоборот. Согласно соотношению (1) в природе объективно не существуют состояния частицы с точно определенными значениями обеих переменных х и рх. Однако одновременно можно определять несопряженные величины: величины y и pz, энергию Е и импульс р (для свободно движущейся в пространстве частицы, когда никакие силы на нее не действуют) и т. д. Согласно второму соотношению (2) для измерения энергии с погрешностью ∆E необходимо время ∆t, не меньшее чем h ∆E. Прохождение частицы через щель. Соотношение неопределенностей проявляется в дифракции частиц. Рассмотрим частицу, свободно движущуюся вдоль оси Y с импульсом pr. До прохождения частицы через щель проекция ее импульса рх имеет точное значение: px = 0. Это значит, что ∆px = 0, а координата х частицы является совершенно неопределенной согласно (2). Соотношение неопределенностей (1) является одним из фундаментальных положений квантовой теории. Из него следует, 1- что невозможно состояние, в котором микрочастица находилась бы в состоянии покоя. 2- при изучении квантового объекта во многих случаях нельзя использовать понятие классической траектории. 3- деление полной энергии квантового объекта на кинетическую и потенциальную часто теряет смысл. Кинетическая энергия Ek зависит от импульса частицы, а потенциальная энергия U – от ее координаты. Однако эти динамические переменные не могут одновременно иметь определенные значения. Поэтому полная энергия Е не может быть представлена в виде суммы одновременно точно определенных кинетической и потенциальной энергий. Таким образом, равенство E = Ek +U для мгновенных значений Ek и U в квантовой механике невозможно, равенство оказывается справедливым для средних значений энергии. Для описания волновых свойств микрочастиц применяют вероятностный подход, т.к. наблюдение волновых явлений несовместимо с представлением о движении частицы по классической траектории. Переход к вероятностному описанию позволяет совместить волновые и корпускулярные свойства материи. Из опытов по дифракции электронов, например, из опытов Джермера следует, что волновые свойства характерны для отдельных микрочастиц. опыты указывают: квадрат модуля амплитуды волн де Бройля в данной точке пространства является мерой того, что частица обнаруживается в этой точке. Там, где интенсивность волн де Бройля >, регистрируется >ee число частиц. Для описания состояния квантовой системы в данный момент времени вводится комплексная волновая функция (пси-функция) Ψ(x, y,z,t). Она определяется так, что вероятность dP нахождения частицы в некоторый момент времени в элементе объема dV прямо пропорциональна Ψ2 и элементу объема dV: Пси-функция определяется с точностью до произвольного постоянного множителя, т. е. функции Ψ и CΨ описывают одно и то же состояние частицы. Пси-функция должна удовлетворять условию нормировки: Волновая функция должна удовлетворять стандартным условиям, находящимся в соответствии с ее вероятностной трактовкой: 1) быть конечной; 2) однозначной; 3) непрерывной; 4) гладкой, т.е. без изломов во всем пространстве, даже в тех точках (линиях, поверхностях), где потенциальная энергия терпит разрыв. частные производные волновой функции могут терпеть разрыв только в тех точках пространства, где потенциальная функция, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода. Принцип суперпозиции квантовых состояний, которому должна удовлетворять волновая функция: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ1, Ψ2, …,Ψn,..., то она также может находиться в состоянии, описываемом линейной комбинацией этих функций:
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.205.114 (0.007 с.) |

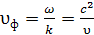 . Следовательно, фазовая скорость этих волн больше скорости света в вакууме, так как c> υ, и не сопоставима с реальной скоростью частицы. Волны де Бройля обладают дисперсией даже в вакууме, поскольку фазовая скорость υф де-бройлевских волн зависит от частоты ω.
. Следовательно, фазовая скорость этих волн больше скорости света в вакууме, так как c> υ, и не сопоставима с реальной скоростью частицы. Волны де Бройля обладают дисперсией даже в вакууме, поскольку фазовая скорость υф де-бройлевских волн зависит от частоты ω.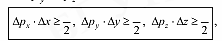 где под неопределенностями координаты и импульса понимают среднеквадратичные отклонения этих физических величин от их средних значений.
где под неопределенностями координаты и импульса понимают среднеквадратичные отклонения этих физических величин от их средних значений.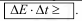 (2)
(2)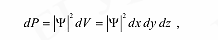 где Ψ2 = ΨΨ*; Ψ* – функция, комплексно сопряженная с Ψ. Волновую функцию Ψ называют амплитудой вероятности. Пси-функция непосредственно не измеряется на опыте. Квадрат модуля функции Ψ задает интенсивность волн де Бройля и является экспериментально наблюдаемой величиной. Физический смысл Ψ2: Ψ2 – это плотность вероятности P, т. е. вероятность нахождения частицы в точке пространства с координатами х, y, z в момент времени t:
где Ψ2 = ΨΨ*; Ψ* – функция, комплексно сопряженная с Ψ. Волновую функцию Ψ называют амплитудой вероятности. Пси-функция непосредственно не измеряется на опыте. Квадрат модуля функции Ψ задает интенсивность волн де Бройля и является экспериментально наблюдаемой величиной. Физический смысл Ψ2: Ψ2 – это плотность вероятности P, т. е. вероятность нахождения частицы в точке пространства с координатами х, y, z в момент времени t: 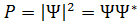 Данная вероятностная интерпретация волновой функции – один из основных постулатов квантовой механики (М. Борн, 1926).
Данная вероятностная интерпретация волновой функции – один из основных постулатов квантовой механики (М. Борн, 1926).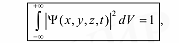 где интеграл берется по всему пространству (−∞,+∞). В этом случае пси-функция Ψ называется нормированной. Условие нормировки волновой функции означает, что пребывание частицы где-либо в бесконечном трехмерном пространстве есть достоверное событие и, следовательно, его вероятность равна единице.
где интеграл берется по всему пространству (−∞,+∞). В этом случае пси-функция Ψ называется нормированной. Условие нормировки волновой функции означает, что пребывание частицы где-либо в бесконечном трехмерном пространстве есть достоверное событие и, следовательно, его вероятность равна единице.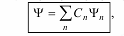 где Cn (n =1, 2, 3,...) – некоторые постоянные коэффициенты (в общем случае комплексные числа). Для нормированных волновых функций
где Cn (n =1, 2, 3,...) – некоторые постоянные коэффициенты (в общем случае комплексные числа). Для нормированных волновых функций 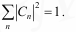 Принцип суперпозиции квантовых состояний лежит в основе физического содержания квантовой механики. С помощью его микроявления описываются без использования классических понятий, которые к ним неприменимы, устраняется противоречие между корпускулярным и волновым описанием явлений.
Принцип суперпозиции квантовых состояний лежит в основе физического содержания квантовой механики. С помощью его микроявления описываются без использования классических понятий, которые к ним неприменимы, устраняется противоречие между корпускулярным и волновым описанием явлений.


 45. Общее и стационарное уравнения Шредингера, их применение для решения физических задач.
45. Общее и стационарное уравнения Шредингера, их применение для решения физических задач.


