
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращательное движение (равномерное, неравномерное) материальной точки. Угловая скорость и ускорение. Связь между линейными и угловыми характеристиками движения.Содержание книги
Поиск на нашем сайте
Вращательное движение (равномерное, неравномерное) материальной точки. Угловая скорость и ускорение. Связь между линейными и угловыми характеристиками движения.
R = ОА – радиус кривизны вращения точки А,
1. Прямолинейное равномерное движение
2. Равномерное движение по окружности
3. Прямолинейное равномерное движение R=
Равномерное движение по окружности:
Неравномерное
a =
Связь между лин. и углов. хар-ми движения:
3. В основе динамики лежат классические законы, Законы Ньютона (сформулированные в 1688г.): ① - Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока действия со стороны других тел не заставит изменить это состояние (выполняется в инерциальной системе). ② - Ускорение тела прямо пропорционально равнодействующей приложенных к нему сил и обратно пропорционально его массе. Тело ускоряется в направлении совпадающем с направлением равнодействующей приложенных сил.
③ - Силы с которыми действуют друг на друга взаимодействующие тела, равны по величине и направлены в противоположные стороны вдоль соединяющей эти точки прямой.
Скорость изменения импульса материальной точки равна действующей на неё силе. Рассмотрим систему из N материальных точек для всех 1-ой: d 2-ой: d … n-ой: d Сложим левые и правые части ур-ния
(
Осевой момент инерции мт и системы мт. Теорема Штейнера. Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси и = сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).Единица измерения СИ: кг·м². При поступат движении мера энертн – масса, а при вращательном-момент энерции. Момент импульса мт:
Oсевым моментом инерции называется величина
a Момент инерц тела выбранной оси а = сумме моментов инерции тел
Идеальный газ. Основное уравнение малекулярно-кинетической теории газов. Идеальный газ-это такой газ, молекулы которого имеют малый собственный объем и не взаимодействуют между собой. Уравнение Клапейрона: Воспользуемся законом Авангарда: при одинаковых давлениях и температурах, моли всех газов занимают одинаковый объем. Это значит, что при P =1,01* P* PV= RT PV = K = PV=ν ν
P= I-ое начало термодинамики Джоуль сформулировал закон: ΔU=Q-A ΔU-изменения внутренней энергии; Q-теплота; A-работа. Этот закон получил название - первое начало термодинамики и является формулировкой закона сохранения энергии. Изменив внутреннею энергию системы за счет теплоты и работы. dU=dQ-dA, dU-бесконечно малое изменение внутренней энергии, происходящее при добавлении к системе БМ. При этом dU,dQ,dA отличаются. dU, dQ не функции параметров системы, а U есть функция параметров системы.
Цикл Карно Рис
Цикл был рассмотрен Карно в 1824г., как идеальный цикл теплового двигателя, который совершает работу за счет теплоты, подводимой к работающему телу в изотермическом процессе. Рабочие тело находится в постоянном контакте с двумя резервуарами с температурой
Рабочее тело в 1 входит в контакт с температурой Адиабатический процесс – процесс, при котором отсутствует теплообмен, т.е. δQ=0, затем газ сжимается изотермически и из 3 переходит в 4состояние. В этот момент тело передает холодильнику тепло Q. После чего переходит адиабатически из 4 в 1. За один полный цикл совершается работа равная площади под кривой цикла. Цикл Карно является обратимым циклом, это значит, что его можно провести по данному направлению 1-4-3-2-1 КПД (формулы): η=1- | |
Тогда формула (4) переписывается: η=1- Теорема Карно: Все обратимые двигатели работающие с одинаковой температурой имеют один и тот же КПД. Ни один необратимый двигатель работающий между теми же термостатами не может иметь больше КПД.
Силовые линии -указывают направление напряженности электростатического поля, т.е. в любой т. Е направлено по касательной силовой линии. -силовые линии проводятся так чтобы величина напряженности поля Е пропорционально линии, ч/з единичную площадку, расположенную перпендикулярно линиям. -они начинаются на “+” зарядах и заканчиваются на “-“.
Напряженность электрического поля системы точечных зарядов = векторной сумме напряженностей полей любого из этих зарядов в отдельности.
Закон Био-Савара-Лапласа В результате обобщения было найдено, что любое магнитное поле может быть вычислено, как векторная сумма полей, создаваемых отдельными элементарными участками токов.
Рисунок
Тепловое излучение и люминесценция. Абсолютно черное тело. Законы Кирхгофа, Стефана-Больцмана. Законы Вина. Квантовая гипотеза. Формула Планка. Колебания электр-их зарядов, входящих в состав вещ-ва, определяют электромагн-ое излуч-ие, котор. сопровождается потерей энергии веществом. При рассеянии и отражении света, формир-ние вторичных световых волн и продолжительность излучения вещ-вом происходит за время, сравнимое с периодом световых колебаний. Если излуч-ие продолжается в течение времени, значительно превышающем период световых колебаний, то возможны 2 типа излучения: люминесценция и тепловое излучение. Люминесценция – это неравновесное излуч-ие, избыточное при данной температуре над тепловым излуч-ием тела и имеющее длительность, > периода световых колебаний. Оно возбуждается внешними источниками энергии. Вещества, способные под действием ɏ рода возбуждений светиться, наз-ся люминофорами. Тепловым излучением наз-ся электромагн-ое излуч-ие, возникающее за счет внутренней энергии излуч-его тела (теплового движения его атомов и молекул) и свойственное всем телам при температурах выше 0 K. Оно зависит от температуры и оптических свойств тела. Тепл. излуч-ие - единствен. вид излуч-ия, котор. может наход-ся в состоянии термодинамического равновесия при опред-ной температуре с телом, испускающим и поглощающим это излуч-ие. Характеристикой теплового излуч-ия, распространяющегося в заданном направлении, является интенсивность излучения. Интенсивность Iλ,T (Iω,T) равновесного излуч-ия при температуре Т – это поток энергии равновесного излучения, рассчитанный на единицу телесного угла (на единичный интервал частот). Индексы – λ (ω) и Т – указывают на зависимость оптической величины от длины волны (частоты) и температуры.
Абсолютно черное тело (АЧТ) - тело, котор. при ɏ температуре полностью поглощает энергию падающих на него электромагн-ых волн независимо от их частоты, поляризации и направления распространения. Тепловое излучение АЧТ является равновесным и изотропным. Его интенсивность одинакова во всех направлениях и не зависит от времени. Спектральное распределение теплового излучения черного тела будет таким же, как у равновесного излучения при той же температуре. Поэтому равновесное излучение часто называют черным излучением. Тепловое излучение имеет сплошной спектр. Зависимость интенсивности Iλ,T излучения черного тела от его длины волны при разных температурах представлена на рис.25.1
Абсолютно черных тел в природе нет, однако тела как сажа и черный бархат, в определенном интервале частот близки к ним. Моделью черного тела является замкнутая полость с небольшим отверстием О, внутренняя поверхность которой зачернена, рис. 25.2. Луч, попавший внутрь такой полости, претерпевает многократные отражения от стенок полости и практически полностью поглощается, так как при каждом отражении происходит частичное поглощение энергии света стенками. Данная модель ближе по характеристикам к черному телу, т.к. больше отношение площади поверхности полости к площади отверстия. Количественной характеристикой теплового излуч-ия служит спектральная плотность энергетической светимости тела Rω,T – мощность излучения с единицы площади поверхности тела в интервале частот 1-ой ширины:
Интегральную энергетическую светимость (энергетическfz светимость) тела определяют так Спектральной характеристикой поглощения телом теплового излучения служит коэффициент поглощения – поглощательная способность тела:
Самопроизвольный процесс передачи энергии в форме теплоты от более нагретого тела к менее нагретому называется теплообменом посредством излучения или радиационным теплообменом. Соотношение между спектральной плотностью энергетической светимости и поглощательной способностью тела определяет закон Кирхгофа (1859): отношение спектральной плотности энергетической светимости к поглощательной способности тела не зависит от природы тела и является универсальной для всех тел функцией частоты и температуры rω,T : Таким образом, учитывая закон следует, что отношение Rω,T / aω,T не зависит от материала тела и равно испускательной способности черного тела rω,T при той же температуре и частоте. Поэтому важной задачей теории теплового излучения является нахождение явной зависимости испускательной способности черного тела от частоты (длины волны) и температуры либо связанной с ней величины, которая в случае равновесного излучения также зависит только от частоты (или длины волны) и температуры: где
Энергетическая светимость черного тела Re зависит только от температуры: σ = 5,67·10-8 Вт/(м2·К4) – постоянная Стефана–Больцмана.
Таким образом, из закона излучения Вина следует, что энергия излучения черного тела распределена по его спектру неравномерно. Кривая спектральной плотности энергетической светимости всегда имеет максимум, который смещается при повышении температуры, рис. 25.3. Закон Стефана–Больцмана ничего не говорит о спектральном составе излучения черного тела. Положение максимума в спектре его излучения описывается экспериментальным законом смещения Вина (1893): длина волны λmax, соответствующая максимальному значению спектральной плотности энергетической светимости rλ,T черного тела, обратно пропорциональна его термодинамической температуре В 1900 г. М. Планк предположил, что теория классического гармонического осциллятора неприменима к атомным (молекулярным) осцилляторам. Он доказал, что формулу для спектральной плотности энергии теплового излучения можно получить, если допустить противоречащую классическим представлениям гипотезу: колебательная энергия атомов излучающего тела квантована. Энергия кванта определяется как где h = 2πh = 6,626·10−34 Дж·с – постоянная Планка – коэффициент пропорциональности между ε и частотой ν; ν – частота колебаний (число полных колебаний за единицу времени); ω – циклическая или круговая частота колебаний (ω = 2πν). Величину h =1,0546·10−34 Дж·с (h перечеркнутая) также называют постоянной Планка. В результате открытия постоянной Планка и связанной с ней идеи квантования физику стали подразделять на классическую и квантовую. Согласно гипотезе Планка энергия атомных (молекулярных) осцилляторов может принимать лишь определенные дискретные значения, кратные hν:
Вращательное движение (равномерное, неравномерное) материальной точки. Угловая скорость и ускорение. Связь между линейными и угловыми характеристиками движения.
R = ОА – радиус кривизны вращения точки А,
1. Прямолинейное равномерное движение
2. Равномерное движение по окружности
3. Прямолинейное равномерное движение R=
Равномерное движение по окружности:
Неравномерное
a =
Связь между лин. и углов. хар-ми движения:
3. В основе динамики лежат классические законы, Законы Ньютона (сформулированные в 1688г.): ① - Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока действия со стороны других тел не заставит изменить это состояние (выполняется в инерциальной системе). ② - Ускорение тела прямо пропорционально равнодействующей приложенных к нему сил и обратно пропорционально его массе. Тело ускоряется в направлении совпадающем с направлением равнодействующей приложенных сил.
③ - Силы с которыми действуют друг на друга взаимодействующие тела, равны по величине и направлены в противоположные стороны вдоль соединяющей эти точки прямой.
Скорость изменения импульса материальной точки равна действующей на неё силе. Рассмотрим систему из N материальных точек для всех 1-ой: d 2-ой: d … n-ой: d Сложим левые и правые части ур-ния
(
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.148 (0.015 с.) |

 =
=  +
+  , где
, где  – нормальное ускорение;
– нормальное ускорение; – тангенциальное ускорение
– тангенциальное ускорение ;
; =
= 



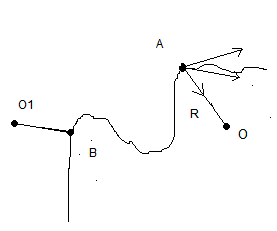
 – скорость в т.А
– скорость в т.А =0,
=0,  =
= 
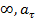 =a=const,
=a=const,  =
= 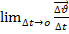 Так как треугольники подобны, то можно записать соотношение
Так как треугольники подобны, то можно записать соотношение
 =
=  , значит
, значит  =
= 
 , значит
, значит 
 =
=  =
= 
 =
= 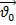 +
+  – направление к центру траектории.
– направление к центру траектории.
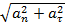
 =
= 
 – const
– const
 = 0
= 0
 +
+ 
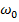 t +
t +  =
=  , [m]=1 кг., [a]=1м/с2, [F]=1H=1 кг·м/с2
, [m]=1 кг., [a]=1м/с2, [F]=1H=1 кг·м/с2 21=-
21=-  =
=  =
=  =
=  =p – импульс
=p – импульс 1/dt =
1/dt =  =
=  =
=  13+
13+ 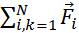 k = 0 – для замкнутой системы
k = 0 – для замкнутой системы i=
i=  – для незамкнутой системы, F – главный вектор внешней силы
– для незамкнутой системы, F – главный вектор внешней силы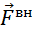 – основной закон динамики поступательного движения системы
– основной закон динамики поступательного движения системы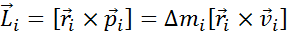 ;
; 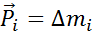 ; Момент импульса тв.тела:
; Момент импульса тв.тела: 

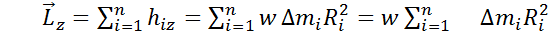

 , равная сумме произведений элементарных масс mi на квадраты их расстояний до оси:
, равная сумме произведений элементарных масс mi на квадраты их расстояний до оси:  , где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
, где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.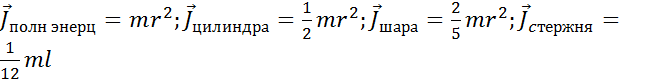
 Теорема Гюйгенса-Штейнера
Теорема Гюйгенса-Штейнера , относительно //-ой ей оси
, относительно //-ой ей оси 

 Па, Т=273К.
Па, Т=273К.  =22,4 литр/моль=22,4*
=22,4 литр/моль=22,4* 
 /моль
/моль
 - закон Клапейрона – Менделеева
- закон Клапейрона – Менделеева =
=  = 1,38*
= 1,38*  (постоянная Больцана);
(постоянная Больцана);  Авагадро
Авагадро KT
KT – концентрация молекул;
– концентрация молекул; – Основное уравнение мкт газов
– Основное уравнение мкт газов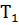 и
и  (
(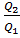 (`4)
(`4) |=νR
|=νR 
 |=νR
|=νR  =|-ν
=|-ν  =|
=| =
= 

 ( математическое выражение теоремы Карно)
( математическое выражение теоремы Карно)


 --принципу суперпозиции полей
--принципу суперпозиции полей

 -магнитная постоянная,
-магнитная постоянная, 

 ,
, 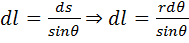 , ds=rdΘ
, ds=rdΘ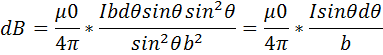
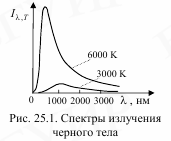 При нормальных температурах тело испускает лишь невидимые глазу инфракрасные лучи, из-за его слабой интенсивности. С повышением Т инфракрасное излучение становится достаточно сильным, и мы ощущаем тепло. При температурах порядка 1000 K тела начинают светиться.
При нормальных температурах тело испускает лишь невидимые глазу инфракрасные лучи, из-за его слабой интенсивности. С повышением Т инфракрасное излучение становится достаточно сильным, и мы ощущаем тепло. При температурах порядка 1000 K тела начинают светиться. При температурах свыше 2000 K раскаленные жидкие или твердые тела испускают желтый или беловатый свет, обладающий сплошным спектром частот. При возрастании температуры тела увеличивается интенсивность его излучения, а также изменяется спектральный состав излучения, рис. 25.1. Максимум интенсивности испускаемого телами теплового излучения смещается в область малых длин волн.
При температурах свыше 2000 K раскаленные жидкие или твердые тела испускают желтый или беловатый свет, обладающий сплошным спектром частот. При возрастании температуры тела увеличивается интенсивность его излучения, а также изменяется спектральный состав излучения, рис. 25.1. Максимум интенсивности испускаемого телами теплового излучения смещается в область малых длин волн. . где
. где  – это энергия излуч-ия, испуск-го за 1 с (мощность излучения) с площади 1 м2 поверхн-ти тела в интервале частот от ω дo ω + dω. в СИ – Джоуль на метр в квадрате (Дж/м2). Спектральную плотность энергетической светимости можно представить в виде функции длины волны λ, поскольку λ =2cπ/ω, то для одного и того же спектрального интервала →
– это энергия излуч-ия, испуск-го за 1 с (мощность излучения) с площади 1 м2 поверхн-ти тела в интервале частот от ω дo ω + dω. в СИ – Джоуль на метр в квадрате (Дж/м2). Спектральную плотность энергетической светимости можно представить в виде функции длины волны λ, поскольку λ =2cπ/ω, то для одного и того же спектрального интервала →  , где
, где  . Знак «минус» указывает, что при возрастании одной из величин (λ или ω) другая величина убывает.
. Знак «минус» указывает, что при возрастании одной из величин (λ или ω) другая величина убывает. .
. которая показывает, какая доля энергии dWω,ω+dω падающего в единицу времени на единицу площади поверхности тела излучения с частотами от ω до ω + dω поглощается телом. Величина aω,T является безразмерной. Согласно опытам Rω,T и aω,T тела зависят от частоты ω соответственно излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Поглощательная способность черного тела для всех частот и температур тождественно равна единице: aω,T ≡1.
которая показывает, какая доля энергии dWω,ω+dω падающего в единицу времени на единицу площади поверхности тела излучения с частотами от ω до ω + dω поглощается телом. Величина aω,T является безразмерной. Согласно опытам Rω,T и aω,T тела зависят от частоты ω соответственно излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Поглощательная способность черного тела для всех частот и температур тождественно равна единице: aω,T ≡1. , где универсальная функция Кирхгофа rω,T есть испускательная способность черного тела (aω,T =1). Энергия, испускаемая черным телом с единицы его поверхности за единицу времени во всех направлениях, т. е. в телесном угле 2π, определяет его испускательную способность: rω,T = π Iω,T .
, где универсальная функция Кирхгофа rω,T есть испускательная способность черного тела (aω,T =1). Энергия, испускаемая черным телом с единицы его поверхности за единицу времени во всех направлениях, т. е. в телесном угле 2π, определяет его испускательную способность: rω,T = π Iω,T . , где с – скорость света в вакууме; uω,T – спектральная плотность энергии равновесного излучения, рассчитанная на единицу интервала частот. uω,T характеризует распределение энергии излучения по частотам при заданной температуре. Интегрируя uω,T по всем частотам, определяют объемную плотность энергии, т. е. полную энергию равновесного излучения в единице объема:
, где с – скорость света в вакууме; uω,T – спектральная плотность энергии равновесного излучения, рассчитанная на единицу интервала частот. uω,T характеризует распределение энергии излучения по частотам при заданной температуре. Интегрируя uω,T по всем частотам, определяют объемную плотность энергии, т. е. полную энергию равновесного излучения в единице объема: 
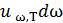 – энергия единицы объема излучения при температуре Т с частотами в интервале от ω до ω + dω. Из закона Кирхгофа энергетическую светимость нечерного тела можно представить как:
– энергия единицы объема излучения при температуре Т с частотами в интервале от ω до ω + dω. Из закона Кирхгофа энергетическую светимость нечерного тела можно представить как:  .
. . Излучение, не подчиняющееся закону Кирхгофа, не является тепловым. Согласно экспериментальному закону Стефана–Больцмана (1884): энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры
. Излучение, не подчиняющееся закону Кирхгофа, не является тепловым. Согласно экспериментальному закону Стефана–Больцмана (1884): энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры  где
где В. Вином была предложена эмпирическая формула для спектральной плотности равновесного излучения. Согласно закону излучения Вина (1896) зависимость универсальной функции Кирхгофа от частоты света и термодинамической температуры имеет вид
В. Вином была предложена эмпирическая формула для спектральной плотности равновесного излучения. Согласно закону излучения Вина (1896) зависимость универсальной функции Кирхгофа от частоты света и термодинамической температуры имеет вид  где а и b – постоянные, определяемые опытным путем.
где а и b – постоянные, определяемые опытным путем. . где b = 2,9·10−3 м·К – постоянная Вина. Из закона смещения Вина (25.9а) следует, что при возрастании температуры положение максимума функции rλ,T смещается в область коротких длин волн, рис. 25.3.
. где b = 2,9·10−3 м·К – постоянная Вина. Из закона смещения Вина (25.9а) следует, что при возрастании температуры положение максимума функции rλ,T смещается в область коротких длин волн, рис. 25.3.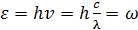
 . Согласно распределению Больцмана вероятность Pn того, что энергия колебания осциллятора частоты ω имеет значение εn при термодинамической температуре Т, определяется выражением
. Согласно распределению Больцмана вероятность Pn того, что энергия колебания осциллятора частоты ω имеет значение εn при термодинамической температуре Т, определяется выражением  где Nn – число осцилляторов с энергией εn; N – полное число осцилляторов;Т – термодинамическая температура; k– постоянная Больцмана. Отсюда можно получить выражение для средней энергии осцилляторов:
где Nn – число осцилляторов с энергией εn; N – полное число осцилляторов;Т – термодинамическая температура; k– постоянная Больцмана. Отсюда можно получить выражение для средней энергии осцилляторов:  и на основе этого показать, что универсальная функция Кирхгофа rω,T будет иметь вид, определяемый формулой Планка:
и на основе этого показать, что универсальная функция Кирхгофа rω,T будет иметь вид, определяемый формулой Планка: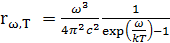 . из формулы Планка можно вывести частные законы, описывающие тепловое излучение: закон излучения Вина выполняющийся в области больших частот (малые длины волн), когда hω Tk>>1. При этом спектральная плотность энергетической светимости черного тела rω,T в шкале частот равна
. из формулы Планка можно вывести частные законы, описывающие тепловое излучение: закон излучения Вина выполняющийся в области больших частот (малые длины волн), когда hω Tk>>1. При этом спектральная плотность энергетической светимости черного тела rω,T в шкале частот равна  , Закон Стефана–Больцмана получается из формулы Планка её интегрированием по частотам:
, Закон Стефана–Больцмана получается из формулы Планка её интегрированием по частотам:  где постоянная Стефана–Больцмана равна
где постоянная Стефана–Больцмана равна 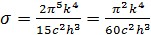 . Закон смещения Вина (25.9а) получается при анализе формулы Планка на экстремум. В результате можно получить:
. Закон смещения Вина (25.9а) получается при анализе формулы Планка на экстремум. В результате можно получить:  .
.


