
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение неопределённости Гейзенберга для координаты и импульсаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Квантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц в заданных внешних полях. Если мерить разные физические величины, то выясняется, что некоторые физ. Величины можно померить в одно время, а другие – нельзя. Волновые свойства частиц и возможность задать для частицы лишь вероятность ее пребывания в данной точке пространства приводят к тому, что сами понятия координаты частицы и ее скорости (или импульса) могут применяться в квантовой механике в ограниченной мере. В этом, вообще говоря, нет ничего удивительного. В классической физике понятие координаты в ряде случаев тоже непригодно для определения положения объекта в пространстве. Например, не имеет смысла говорить о том, что электромагнитная волна находится в данной точке пространства или что положение фронта волновой поверхности на воде характеризуется координатами x, y, z. Корпускулярно-волновая двойственность свойств частиц, изучаемых в квантовой механике, приводит к тому, что в ряде случаев оказывается невозможным, в классическом смысле, одновременно характеризовать частицу ее положением в пространстве (координатами) и скоростью (или импульсом). Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса. Неопределенности значений x и удовлетворяют соотношению:
Из (4.2.1) следует, что чем меньше неопределенность одной величины (x или), тем больше неопределенность другой. Возможно, такое состояние, в котором одна их переменных имеет точное значение (), другая переменная при этом оказывается совершенно неопределенной (– ее неопределенность равна бесконечности), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременного измерения координаты и импульса микрообъекта с любой наперед заданной точностью. Соотношение, аналогичное (4.2.1), имеет место для y и, для z и, а также для других пар величин (в классической механике такие пары называются канонически сопряженными). Обозначив канонически сопряженные величины буквами A и B, можно записать:
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга. Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей:
Это соотношение означает, что определение энергии с точностью должно занять интервал времени, равный, по меньшей мере, . Волновые функции Функция описывает вероятность найти частицу в данной точке пространства. Первый постулат квантовой механики: Состояние частицы в квантовой механике описывается заданием волновой функции Аппарат, разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией Вероятностный смысл волновой функции. Невозможность задания состояния микрочастицы указанием в любой момент времени ее координат и скорости и отказ от траекторного способа описания движения приводит к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике, определяя состояние частицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени. В 1926 г. М.Борн так сформулировал вероятностный смысл волновой функции в квантовой механике: Квадрат модуля волновой функции Следовательно
Отметим, что волновая функция в общем случае является комплекснозначной функцией, то есть содержит действительную и мнимую части. Физический смысл, поэтому, имеет не сама волновая функция, а ее квадрат модуля Уравнение Шрёдингера 1. Свободное одномерное движение частицы, т.е. частица находится в поле с постоянным потенциалом и ее потенциальная энергия равна нулю. В этом случае уравнение (III.9) примет вид:
или, после несложных преобразований,
где
где
Теперь несколько усложним задачу и рассмотрим 2. Движение частицы в яме с бесконечно высокими стенками. В этом случае потенциальная энергия будет равна
где а - ширина потенциальной ямы. Уравнение Шредингера (III.9) разобьется на два: для интервала x<0 и x>a и примет вид:
и может быть удовлетворено лишь функцией
Решением уравнения (III.11) при дополнительных условиях (III.15) будет функция (III.12), однако константы
это возможно только когда
Рассмотрим теперь второе граничное условие -
или
Представим теперь экспоненту в виде тригонометрических функций согласно формуле Эйлера:
(необходимо помнить, что
Приведя подобные, мы это уравнение сведем к виду
Равенство (III.19) справедливо при условии
где n - любое целое число.
Итак, волновая функция частицы в потенциальной яме принимает вид
С другой стороны, из
следует, что энергия частицы может принимать следующие значения:
т.е. энергия частицы является дискретной. 3. Рассмотрим теперь одномерное движение частицы по оси x под воздействием упругой возвращающей силы
Положим для определенности
Если ввести обозначения
Непосредственно найти решения этого уравнения нельзя, поэтому предположим, что
которое имеет решения вида
Подстановка этой функции в исходное уравнение (III.25) дает
При четных значениях величины
.........................................
а для собственных функций и собственных значений гармонического осциллятора мы получим выражения:
Квантовые числа Квантовое число n – главное. Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He+, Li2+ и т. д.). В этом случае энергия электрона
где n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном. В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.
Орбитальное квантовое число l характеризует форму орбиталей и принимает значения от 0 до n – 1. Кроме числовых l имеет буквенные обозначения
Электроны с одинаковым значением l образуют подуровень. Квантовое число l определяет квантование орбитального момента количества движения электрона Квантовое число ml называют магнитным. Оно определяет пространственное расположение атомной орбитали и принимает целые значения от –l до +l через нуль, то есть 2l + 1 значений. Расположение орбитали характеризуется значением проекции вектора орбитального момента количества движения Mz на какую-либо ось координат (обычно ось z):
Все вышесказанное можно представить таблицей:
Орбитали одного подуровня (l = const) имеют одинаковую энергию. Такое состояние называют вырожденным по энергии. Так p-орбиталь – трехкратно, d – пятикратно, а f – семикратно вырождены. Граничные поверхности s-, p-, d-, f- орбиталей показаны на рис. 2.1.
s-Орбитали сферически симметричны для любого n и отличаются друг от друга только размером сферы. Их максимально симметричная форма обусловлена тем, что при l = 0 и μl = 0. p-Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: ml = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются px, py, pz. d-Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором ml = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются dz² и dx²–y², а ориентированные лопастями по биссектрисам координатных углов – dxy, dyz, dxz. Семь f-орбиталей, соответствующих l = 3 (n ≥ 4), изображаются в виде граничных поверхностей, приведенных на рис. 2.1. Квантовые числа n, l и ml не полностью характеризуют состояние электрона в атоме. Экспериментально установленно, что электрон имеет еще одно свойство – спин. Упрощенно спин можно представить как вращение электрона вокруг собственной оси. Спиновое квантовое число ms имеет только два значения ms = ±1/2, представляющие собой две проекции углового момента электрона на выделенную ось. Электроны с разными ms обозначаются стрелками, направленными вверх В многоэлектронных атомах, как и в атоме водорода, состояние электрона определяется значениями тех же четырех квантовых чисел, однако в этом случае электрон находится не только в поле ядра, но и в поле других электронов. Поэтому энергия в многоэлектронных атомах определяется не только главным, но и орбитальным квантовым числом, а вернее их суммой: энергия атомных орбиталей возрастает по мере увеличения суммы n + l; при одинаковой сумме сначала заполняется уровень с меньшим n и большим l. Энергия атомных орбиталей возрастает согласно ряду
Итак, четыре квантовых числа описывают состояние электрона в атоме и характеризуют энергию электрона, его спин, форму электронного облака и его ориентацию в пространстве. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.72 (0.009 с.) |

 , являющейся функцией пространственных координат и времени.
, являющейся функцией пространственных координат и времени. , получать полную информацию о движении микрочастицы.
, получать полную информацию о движении микрочастицы. того, что в момент времени
того, что в момент времени  частица может быть обнаружена в точке пространства
частица может быть обнаружена в точке пространства 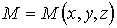 с координатами
с координатами  ,
,  и
и  .
. .
.
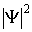 - действительная величина, которую во многих случаях удобно находить, умножая волновую функцию
- действительная величина, которую во многих случаях удобно находить, умножая волновую функцию 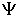 на комплексно сопряженную ей функцию
на комплексно сопряженную ей функцию  , так как из теории комплексных чисел следует, что
, так как из теории комплексных чисел следует, что  .
. , (III.10)
, (III.10) , (III.11)
, (III.11) - некоторая постоянная. Решением такого дифференциального уравнения (дифференциальное уравнение второго порядка с постоянными коэффициентами) хорошо известно и в общем случае имеет вид:
- некоторая постоянная. Решением такого дифференциального уравнения (дифференциальное уравнение второго порядка с постоянными коэффициентами) хорошо известно и в общем случае имеет вид: , (III.12)
, (III.12) и
и 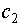 - произвольные постоянные. Легко убедится, что в данном случае на E не накладывается никаких ограничений и энергетический спектр непрерывен.
- произвольные постоянные. Легко убедится, что в данном случае на E не накладывается никаких ограничений и энергетический спектр непрерывен.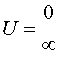
 (III.13)
(III.13)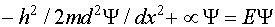 , (III.14)
, (III.14) , т.е. частица не может находится за пределами потенциальной ямы. Для интервала 0<x<a уравнение Шредингера будет идентично (III.11), но с граничными условиями
, т.е. частица не может находится за пределами потенциальной ямы. Для интервала 0<x<a уравнение Шредингера будет идентично (III.11), но с граничными условиями (III.15)
(III.15) следует
следует (III.16)
(III.16)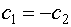
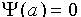 :
: (III.17)
(III.17)
 (III.18)
(III.18)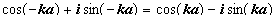 )
) , где
, где  (III.19)
(III.19)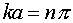 , или
, или  (III.20)
(III.20) (III.21)
(III.21) (III.22)
(III.22) (III.23)
(III.23) , где k - силовая постоянная. Такая система называется линейным гармоническим осциллятором.
, где k - силовая постоянная. Такая система называется линейным гармоническим осциллятором. , где
, где  - частота колебаний, можно записать уравнение Шредингера для линейного гармонического осциллятора:
- частота колебаний, можно записать уравнение Шредингера для линейного гармонического осциллятора: (III.24)
(III.24) и
и  , то (III.24) примет вид:
, то (III.24) примет вид: (III.25)
(III.25) , (это справедливо, когда амплитуда колебаний не велика). В этом случае (III.25) перейдет в уравнение
, (это справедливо, когда амплитуда колебаний не велика). В этом случае (III.25) перейдет в уравнение (III.26)
(III.26)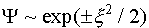 . Однако поскольку волновая функция должна быть ограниченной, то физический смысл имеет только экспонента с отрицательным показателем:
. Однако поскольку волновая функция должна быть ограниченной, то физический смысл имеет только экспонента с отрицательным показателем: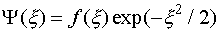 (III.27)
(III.27)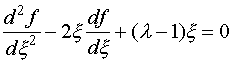 (III.28)
(III.28) ,
, 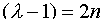 это уравнение есть хорошо известное уравнение Эрмита, решениями которого для n=0,1,2... являются функции
это уравнение есть хорошо известное уравнение Эрмита, решениями которого для n=0,1,2... являются функции  , называемыми полиномами Эрмита. Для низших n полиномы Эрмита имеют вид:
, называемыми полиномами Эрмита. Для низших n полиномы Эрмита имеют вид: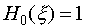

 (III.29)
(III.29)
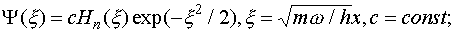 (III.30)
(III.30) (III.31)
(III.31)



 в сферически симметричном кулоновском поле ядра.
в сферически симметричном кулоновском поле ядра.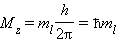
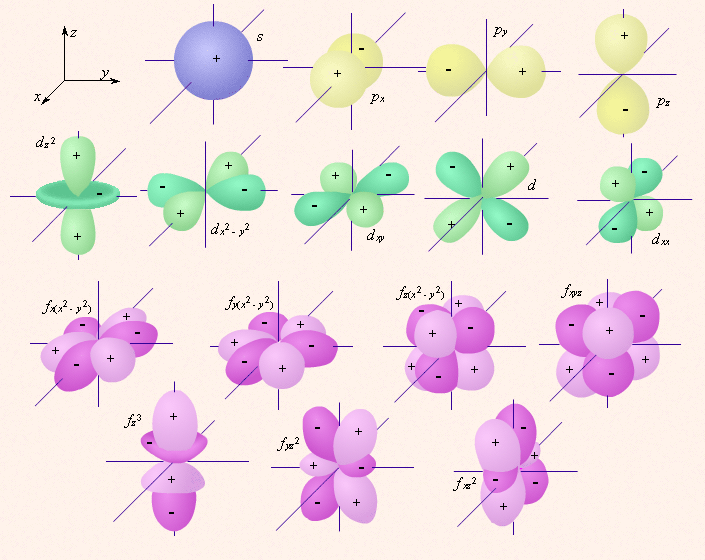
 и вниз
и вниз  .
.


