Волновые свойства микрочастиц.

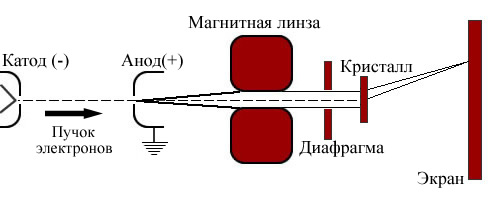
Развитие представлений о корпускулярно-волновых свойствах материи получило в гипотезе о волновом характере движения микрочастиц. Луи де Бройль из идеи симметрии в природе для частиц вещества и света приписал любой микрочастице некий внутренний периодический процесс (1924). Объединив формулы E = hν и E = mc², он получил соотношение, показывающее, что любой частице соответствует своя длина волны: λ_Б= h/mv = h/p, где p- импульс волны-частицы. К примеру, для электрона, имеющего энергию 10 эВ, длина волны де Бройля составляет 0,388 нм.
В дальнейшем было показано, что состояние микрочастицы в квантовой механике может быть описано определенной комплексной волновой функцией координат Ψ(q), причем квадрат модуля этой функции |Ψ|²определяет распределение вероятностей значений координат. Эта функция была впервые введена в квантовую механику Шредингером в 1926 г. Таким образом, волна де Бройля не несет энергию, а только отображает “распределение фаз” некоего вероятностного периодического процесса в пространстве. Следовательно, описание состояния объектов микромира носит вероятностный характер, в отличие от объектов макромира, которые описываются законами классической механики.

Для доказательства идеи де Бройля о волновой природе микрочастиц немецкий физик Эльзассер предложил использовать кристаллы для наблюдения дифракции электронов (1925). В США К. Дэвиссон и Л. Джермер обнаружили явление дифракции при прохождении пучка электронов через пластинку из кристалла никеля (1927). Независимо от них дифракцию электронов при прохождении через металлическую фольгу открыли Дж. П. Томсон в Англии и П.С. Тартаковский в СССР. Так идея де Бройля о волновых свойствах вещества нашла экспериментальное подтверждение. Впоследствии дифракционные, а значит волновые, свойства были обнаружены у атомных и молекулярных пучков. Корпускулярно-волновыми свойствами обладают не только фотоны и электроны, но и все микрочастицы.

Октрытие волновых свойств у микрочастиц показало, что такие формы материи, как поле (непрерывное) и вещество (дискретное), которые с точки зрения классической физики, считались качественно отличающимися, в определенных условиях могут проявлять свойства, присущие и той и другой форме. Это говорит о единстве этих форм материи. Полное описание их свойств возможно только на основе противоположных, но дополняющих друг - друга представлений.

Дифракция электронов.

Для получения спектра световых волн и определения их длины используется дифракционная решетка. Она представляет собой совокупность большого числа узких щелей, разделенных непрозрачными промежутками, например, стеклянная пластинка с нанесенными на ней царапинами (штрихами). Как и от двух щелей (смотри лаб. работу 2), при прохождении через такую решетку плоской монохроматической волны, каждая щель станет источником вторичных когерентных волн, в результате сложения которых возникнет интерференционная картина. Условие возникновения максимумов интерференции на экране, расположенном на расстоянии L от дифракционной решетки, определяется разностью хода между волнами от соседних щелей. Если в точке наблюдения разность хода будет равна целому числу волн, то произойдет их усиление и будет наблюдаться максиму интерференционной картины. Расстояние между максимумами для света определенной длины волны λ определяется по формуле: h₀ = λL/d. Величина d называется периодом решетки и равна сумме ширины прозрачного и непрозрачного промежутков. Для наблюдения дифракции электронов в качестве естественной дифракционной решетки используют кристаллы металла. Периоду d такой естественной дифракционной решетки соответствует характерное расстояние между атомами кристалла.

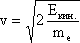Схема установки для наблюдения электронной дифракции приведена на рисунке 1. Проходя разность потенциалов U между катодом и анодом, электроны приобретают кинетическую энергию E_кин. = Ue, где e - заряд электрона. Из формулы кинетической энергии E_кин. = (m_ev²)/2 можно найти скорость электрона: . Зная массу электрона m_e можно определить его импульс и соответственно длину волны де Бройля.