
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектры излучения водородоподобных атомовСодержание книги
Поиск на нашем сайте Излучение и поглощение энергии атомом Боровская модель атома Материал из Википедии — свободной энциклопедии Перейти к: навигация, поиск
Боровская модель водородоподобного атома (Z — заряд ядра), где отрицательно заряженный электрон заключен в атомной оболочке, окружающей малое, положительно заряженное атомное ядро. Переход электрона с орбиты на орбиту сопровождается излучением или поглощением кванта электромагнитной энергии (hν). Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]: Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты
Здесь Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера, решая задачу о движении электрона в центральном кулоновском поле. Радиус первой орбиты в атоме водорода R0=5,2917720859(36)·10−11 м[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты Опыт Штерна–Герлаха Опыт Штерна — Герлаха — опыт немецких физиков Отто Штерна и Вальтера Герлаха, осуществлённый в 1922 году. Опыт подтвердил наличие у атомов спина (изначально в эксперименте участвовали атомы серебра, а потом и других металлов) и факт пространственного квантования направления их магнитных моментов. Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянным магнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов. Опыт Штерна–Герлаха Опыт Штерна — Герлаха — опыт немецких физиков Отто Штерна и Вальтера Герлаха, осуществлённый в 1922 году. Опыт подтвердил наличие у атомов спина (изначально в эксперименте участвовали атомы серебра, а потом и других металлов) и факт пространственного квантования направления их магнитных моментов. Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянным магнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово-механической теории о квантовании магнитного момента атомов.
Во многих современных учебниках и монографиях приводится вот такая схема опыта.
Атомы серебра испаряются в печи и, пролетая в вакууме через отверстия нескольких диафрагм, попадают в поле магнита, один полюс которого плоский, другой заострен. Утверждается, что такая геометрия полюсов создает сильно неоднородный магнитный поток. На атом водорода с магнитным моментом и движущимся в сильно неоднородном магнитном поле напряженностью H вдоль линии Z соединяющей полюса магнита действует сила F=m dH/dZ, отклоняющая его от первоначального направления движения. Обнаружено расщепление пучка на две компоненты симметричные относительно первичного направления пучка и отстоящие от него на величину D. Величина магнитного момента пропорциональна смещению и равна магнетону Бора. Формула пространственного квантования проекции mz на линию полюсов магнита магнитного момента атома m0: mz=m0m (m=0-+1,…) отсюда гипотеза о существовании собственного механического момента электрона – спина. Спин электрона Спин (от англ. spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы. Спин измеряется в единицах В связи с этим говорят о целом или полуцелом спине частицы. Дифракция электронов. Для получения спектра световых волн и определения их длины используется дифракционная решетка. Она представляет собой совокупность большого числа узких щелей, разделенных непрозрачными промежутками, например, стеклянная пластинка с нанесенными на ней царапинами (штрихами). Как и от двух щелей (смотри лаб. работу 2), при прохождении через такую решетку плоской монохроматической волны, каждая щель станет источником вторичных когерентных волн, в результате сложения которых возникнет интерференционная картина. Условие возникновения максимумов интерференции на экране, расположенном на расстоянии L от дифракционной решетки, определяется разностью хода между волнами от соседних щелей. Если в точке наблюдения разность хода будет равна целому числу волн, то произойдет их усиление и будет наблюдаться максиму интерференционной картины. Расстояние между максимумами для света определенной длины волны λ определяется по формуле: h0 = λL/d. Величина d называется периодом решетки и равна сумме ширины прозрачного и непрозрачного промежутков. Для наблюдения дифракции электронов в качестве естественной дифракционной решетки используют кристаллы металла. Периоду d такой естественной дифракционной решетки соответствует характерное расстояние между атомами кристалла. Схема установки для наблюдения электронной дифракции приведена на рисунке 1. Проходя разность потенциалов U между катодом и анодом, электроны приобретают кинетическую энергию Eкин. = Ue, где e - заряд электрона. Из формулы кинетической энергии Eкин. = (mev2)/2 можно найти скорость электрона: Волновые функции Функция описывает вероятность найти частицу в данной точке пространства. Первый постулат квантовой механики: Состояние частицы в квантовой механике описывается заданием волновой функции Аппарат, разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией Вероятностный смысл волновой функции. Невозможность задания состояния микрочастицы указанием в любой момент времени ее координат и скорости и отказ от траекторного способа описания движения приводит к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике, определяя состояние частицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени. В 1926 г. М.Борн так сформулировал вероятностный смысл волновой функции в квантовой механике: Квадрат модуля волновой функции Следовательно
Отметим, что волновая функция в общем случае является комплекснозначной функцией, то есть содержит действительную и мнимую части. Физический смысл, поэтому, имеет не сама волновая функция, а ее квадрат модуля Уравнение Шрёдингера 1. Свободное одномерное движение частицы, т.е. частица находится в поле с постоянным потенциалом и ее потенциальная энергия равна нулю. В этом случае уравнение (III.9) примет вид:
или, после несложных преобразований,
где
где
Теперь несколько усложним задачу и рассмотрим 2. Движение частицы в яме с бесконечно высокими стенками. В этом случае потенциальная энергия будет равна
где а - ширина потенциальной ямы. Уравнение Шредингера (III.9) разобьется на два: для интервала x<0 и x>a и примет вид:
и может быть удовлетворено лишь функцией
Решением уравнения (III.11) при дополнительных условиях (III.15) будет функция (III.12), однако константы
это возможно только когда
Рассмотрим теперь второе граничное условие -
или
Представим теперь экспоненту в виде тригонометрических функций согласно формуле Эйлера:
(необходимо помнить, что
Приведя подобные, мы это уравнение сведем к виду
Равенство (III.19) справедливо при условии
где n - любое целое число.
Итак, волновая функция частицы в потенциальной яме принимает вид
С другой стороны, из
следует, что энергия частицы может принимать следующие значения:
т.е. энергия частицы является дискретной. 3. Рассмотрим теперь одномерное движение частицы по оси x под воздействием упругой возвращающей силы
Положим для определенности
Если ввести обозначения
Непосредственно найти решения этого уравнения нельзя, поэтому предположим, что
которое имеет решения вида
Подстановка этой функции в исходное уравнение (III.25) дает
При четных значениях величины
.........................................
а для собственных функций и собственных значений гармонического осциллятора мы получим выражения:
Квантовые числа Квантовое число n – главное. Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He+, Li2+ и т. д.). В этом случае энергия электрона
где n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном. В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.
Орбитальное квантовое число l характеризует форму орбиталей и принимает значения от 0 до n – 1. Кроме числовых l имеет буквенные обозначения
Электроны с одинаковым значением l образуют подуровень. Квантовое число l определяет квантование орбитального момента количества движения электрона Квантовое число ml называют магнитным. Оно определяет пространственное расположение атомной орбитали и принимает целые значения от –l до +l через нуль, то есть 2l + 1 значений. Расположение орбитали характеризуется значением проекции вектора орбитального момента количества движения Mz на какую-либо ось координат (обычно ось z):
Все вышесказанное можно представить таблицей:
Орбитали одного подуровня (l = const) имеют одинаковую энергию. Такое состояние называют вырожденным по энергии. Так p-орбиталь – трехкратно, d – пятикратно, а f – семикратно вырождены. Граничные поверхности s-, p-, d-, f- орбиталей показаны на рис. 2.1.
s-Орбитали сферически симметричны для любого n и отличаются друг от друга только размером сферы. Их максимально симметричная форма обусловлена тем, что при l = 0 и μl = 0. p-Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: ml = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются px, py, pz. d-Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором ml = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются dz² и dx²–y², а ориентированные лопастями по биссектрисам координатных углов – dxy, dyz, dxz. Семь f-орбиталей, соответствующих l = 3 (n ≥ 4), изображаются в виде граничных поверхностей, приведенных на рис. 2.1. Квантовые числа n, l и ml не полностью характеризуют состояние электрона в атоме. Экспериментально установленно, что электрон имеет еще одно свойство – спин. Упрощенно спин можно представить как вращение электрона вокруг собственной оси. Спиновое квантовое число ms имеет только два значения ms = ±1/2, представляющие собой две проекции углового момента электрона на выделенную ось. Электроны с разными ms обозначаются стрелками, направленными вверх В многоэлектронных атомах, как и в атоме водорода, состояние электрона определяется значениями тех же четырех квантовых чисел, однако в этом случае электрон находится не только в поле ядра, но и в поле других электронов. Поэтому энергия в многоэлектронных атомах определяется не только главным, но и орбитальным квантовым числом, а вернее их суммой: энергия атомных орбиталей возрастает по мере увеличения суммы n + l; при одинаковой сумме сначала заполняется уровень с меньшим n и большим l. Энергия атомных орбиталей возрастает согласно ряду
Итак, четыре квантовых числа описывают состояние электрона в атоме и характеризуют энергию электрона, его спин, форму электронного облака и его ориентацию в пространстве. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии. Спектры излучения водородоподобных атомов Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии (тev 2 / 2) и потенциальной энергии в электростатическом поле ядра (– Ze 2/(4pe0 r)):
(учли, что
где знак минус означает, что электрон находится в связанном состоянии. Из формулы (212.3) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Целое число n в выражении (212.3), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n =1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными. Придавая n различные целочисленные значения, получим для атома водорода (Z = 1), согласно формуле (212.3), возможные уровни энергии, схематически представленные на рис. 294. Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = ¥. Атом водорода обладает, таким образом, минимальной энергией (E 1 = –13,55 эВ) при n = 1 и максимальной (Е ¥ = 0) при n = ¥. Следовательно, значение Е ¥ = 0 соответствует ионизации атома (отрыву от него электрона). Согласно второму постулату Бора (см. (210.2)), при переходе атома водорода (Z= 1) из стационарного состояния л в стационарное состояние т с меньшей энергией испускается квант
откуда частота излучения
где R = mee 4/(8 h 3 Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в эмпирических формулах для атома водорода. Это совпадение убедительно доказывает правильность полученной Бором формулы (212.3) для энергетических уровней водородоподобной системы. Подставляя, например, в формулу (212.4) т= 1 и п= 2, 3, 4,..., получим группу линий, образующих серию Лаймана (см. § 209) и соответствующих переходам электронов с возбужденных уровней (n = 2, 3, 4,...) на основной (m = l). Аналогично, при подстановке m = 2, 3, 4, 5, 6 и соответствующих им значений n получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис. 294). Следовательно, по теории Бора, количественно объяснившей спектр атома водорода, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний, расположенных выше данного.
Спектр поглощения атома водорода является линейчатым, но содержит при нормальных условиях только серию Лаймана. Он также объясняется теорией Бора. Так как свободные атомы водорода обычно находятся в основном состоянии (стационарное состояние с наименьшей энергией при n = 1), то при сообщении атомам извне определенной энергии могут наблюдаться лишь переходы атомов из основного состояния в возбужденные (возникает серия Лаймана). Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями (с одной стороны, применяет законы классической физики, а с другой — основывается на квантовых постулатах). В теории Бора рассмотрены спектры атома водорода и водородоподобных систем и вычислены частоты спектральных линий, однако эта теория не смогла объяснить интенсивности спектральных линий и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора была невозможность описания с ее помощью спектра атома гелия — одного из простейших атомов, непосредственно следующего за атомом водорода.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1474; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |



 .
. и энергии
и энергии  находящегося на этой орбите электрона:
находящегося на этой орбите электрона: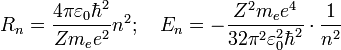
 — масса электрона, Z — количество протонов в ядре,
— масса электрона, Z — количество протонов в ядре,  — диэлектрическая постоянная, e — заряд электрона.
— диэлектрическая постоянная, e — заряд электрона. эВ представляет собой энергию ионизации атома водорода
эВ представляет собой энергию ионизации атома водорода
 (приведённой постоянной Планка, или постоянной Дирака) и равен
(приведённой постоянной Планка, или постоянной Дирака) и равен 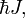 где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).
где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).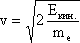 . Зная массу электрона me можно определить его импульс и соответственно длину волны де Бройля.
. Зная массу электрона me можно определить его импульс и соответственно длину волны де Бройля. 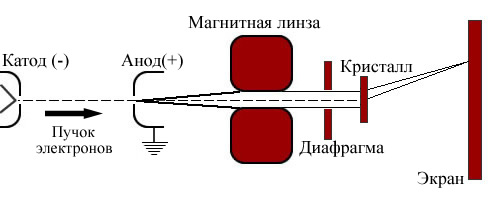
 , являющейся функцией пространственных координат и времени.
, являющейся функцией пространственных координат и времени. , получать полную информацию о движении микрочастицы.
, получать полную информацию о движении микрочастицы. того, что в момент времени
того, что в момент времени  частица может быть обнаружена в точке пространства
частица может быть обнаружена в точке пространства 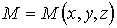 с координатами
с координатами  ,
,  и
и  .
. .
.
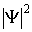 - действительная величина, которую во многих случаях удобно находить, умножая волновую функцию
- действительная величина, которую во многих случаях удобно находить, умножая волновую функцию 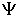 на комплексно сопряженную ей функцию
на комплексно сопряженную ей функцию  , так как из теории комплексных чисел следует, что
, так как из теории комплексных чисел следует, что  .
. , (III.10)
, (III.10) , (III.11)
, (III.11) - некоторая постоянная. Решением такого дифференциального уравнения (дифференциальное уравнение второго порядка с постоянными коэффициентами) хорошо известно и в общем случае имеет вид:
- некоторая постоянная. Решением такого дифференциального уравнения (дифференциальное уравнение второго порядка с постоянными коэффициентами) хорошо известно и в общем случае имеет вид: , (III.12)
, (III.12) и
и 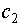 - произвольные постоянные. Легко убедится, что в данном случае на E не накладывается никаких ограничений и энергетический спектр непрерывен.
- произвольные постоянные. Легко убедится, что в данном случае на E не накладывается никаких ограничений и энергетический спектр непрерывен.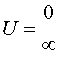
 (III.13)
(III.13)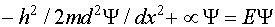 , (III.14)
, (III.14) , т.е. частица не может находится за пределами потенциальной ямы. Для интервала 0<x<a уравнение Шредингера будет идентично (III.11), но с граничными условиями
, т.е. частица не может находится за пределами потенциальной ямы. Для интервала 0<x<a уравнение Шредингера будет идентично (III.11), но с граничными условиями (III.15)
(III.15) следует
следует (III.16)
(III.16)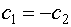
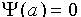 :
: (III.17)
(III.17)
 (III.18)
(III.18)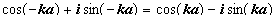 )
) , где
, где  (III.19)
(III.19)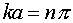 , или
, или  (III.20)
(III.20) (III.21)
(III.21) (III.22)
(III.22) (III.23)
(III.23) , где k - силовая постоянная. Такая система называется линейным гармоническим осциллятором.
, где k - силовая постоянная. Такая система называется линейным гармоническим осциллятором. , где
, где  - частота колебаний, можно записать уравнение Шредингера для линейного гармонического осциллятора:
- частота колебаний, можно записать уравнение Шредингера для линейного гармонического осциллятора: (III.24)
(III.24) и
и  , то (III.24) примет вид:
, то (III.24) примет вид: (III.25)
(III.25) , (это справедливо, когда амплитуда колебаний не велика). В этом случае (III.25) перейдет в уравнение
, (это справедливо, когда амплитуда колебаний не велика). В этом случае (III.25) перейдет в уравнение (III.26)
(III.26)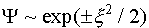 . Однако поскольку волновая функция должна быть ограниченной, то физический смысл имеет только экспонента с отрицательным показателем:
. Однако поскольку волновая функция должна быть ограниченной, то физический смысл имеет только экспонента с отрицательным показателем: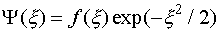 (III.27)
(III.27)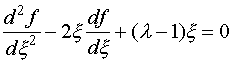 (III.28)
(III.28) ,
, 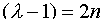 это уравнение есть хорошо известное уравнение Эрмита, решениями которого для n=0,1,2... являются функции
это уравнение есть хорошо известное уравнение Эрмита, решениями которого для n=0,1,2... являются функции  , называемыми полиномами Эрмита. Для низших n полиномы Эрмита имеют вид:
, называемыми полиномами Эрмита. Для низших n полиномы Эрмита имеют вид: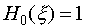

 (III.29)
(III.29)
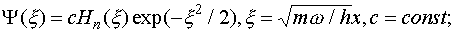 (III.30)
(III.30) (III.31)
(III.31)



 в сферически симметричном кулоновском поле ядра.
в сферически симметричном кулоновском поле ядра.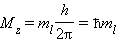
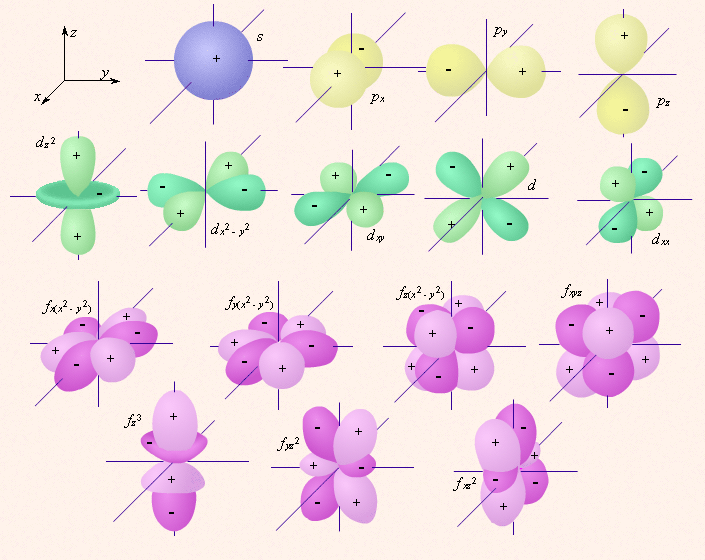
 и вниз
и вниз  .
.
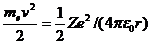 ; см. (208.1)). Учитывая квантованные для радиуса n -й стационарной орбиты значения (212.1), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
; см. (208.1)). Учитывая квантованные для радиуса n -й стационарной орбиты значения (212.1), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения: (212.3)
(212.3)
 (212.4)
(212.4) ).
).



