
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение неопределенностей ГейзенбергаСодержание книги
Поиск на нашем сайте
Соотношение неопределенности Гейзенберга представляется как одно из основных, фундаментальных положений квантовой механики. Точка зрения Ландау отражает распространенное мнение о соотношении неопределенности Гейзенберга. Рассмотрим положения, в основном, сформулированные авторами квантовой механики, связанными с изложением и трактовкой этого соотношения, которые могут оправдать приведенную характеристику. 1. “Классическая физика как раз и кончается в том месте, где нельзя уже отказаться от учета влияния наблюдателя на исследуемые процессы”,“Невозможность отдалить самостоятельное поведение от их взаимодействия с измерительными приборами, предназначенных для изучения условий протекания явления, влечет за собой неоднозначность в приписывании обычных атрибутов атомным явлениям. Это обстоятельство вызывает необходимость пересмотра нашего отношения к проблеме физического объяснения”. Данный фактор, в действительности, имеет место и в процессе обычных измерений, описываемых с помощью классической механики. Но влияние измерительного прибора и методики измерения либо учитывается и вводится поправка, либо результат измерений фигурирует как условный, т. е. оговаривается методика. Во всяком случае, этот фактор достаточно очевидный и не выглядит парадоксальным. 2. “Специфическая неточность, обусловленная соотношением неопределенности, в классической физике отсутствует”. “В квантовой механике мы встречаемся с парадоксальной ситуацией — наблюдаемые события повинуются закону случая… Сегодня порядок идей обратный [по сравнению с “предвзятыми идеями о причинности”]: случайность стала первичным понятием”. “С точки зрения квантовой теории нет никакой причины, по которой [например] распались имменно эти ядра, они распались “просто так”, спонтанно. Квантовая теория предсказывает лишь вероятность распада ядер”. В данном случае отрицается наличие причины происходящих явлений. Это часто используемый в квантовой механике способ “решения научных задач”: проблема “закрывается” путем провозглашения соответствующего “закона” или “принципа”. Для Борна “детерминизм” являлся ярлыком, характеризующим неприятие “современной” науки. Его совершенно не устраивала и “компромиссная” теория “скрытых переменных”. В основе мистического миропонимания лежит аналогичное восприятие необъяснимого: подразумевается, что феномен, недоступный нашему пониманию, находится вне сферы возможности его объяснения. Следует отметить, что не все классики квантовой механики придерживались этой теории, в частности, против нее решительно выступал Планк: “eсли подобный шаг оказался бы действительно необходимым, то тем самым цель физического исследования была бы значительно отброшена назад, что нанесло бы значительный ущерб, значение которого нетрудно оценить”. Тем не менее, подобное толкование “принципа неопределенности” вошло в ортодоксальную науку. 3. Соотношение неопределенности ряд авторов рассматривал как отражение волновых свойств частиц — следствие корпускулярно-волнового дуализма. “Соотношения неопределенности Гейзенберга непосредственно вытекают из положения, что элементами новой картины мира являются не материальные частицы, а простейшие периодические волны материи”. “Соотношения неопределенности следуют из способа которым связываются с помощью постоянной h корпускулярная и волновая сторона единых объектов вещества и излучения”. Однако эта точка зрения не является обоснованной, о чем, в частности, свидетельствует вывод соотношения Гейзенбергом без “непосредственного обращения к волновой картине с помощью математической схемы квантовой теории”. 4. Соотношение неопределенности Гейзенберга показывает, что “между точностью, с которой одновременно может быть установлено положение частицы, и точностью ее импульса существует определенное соотношение”: qp ≥ h, (1) О неприятии данного соотношения в период становления квантовой теории свидетельствуют дискуссии между Эйнштейном и Бором и, в частности, т. н. “парадокс Эйнштейна – Подольского – Розена”, в котором предполагается “мысленное” одновременное измерение импульса и координаты у двух частиц – “двойников”. Характерная деталь: анализ приведенного выражения проводится так, как будто это эмпирическая формула, а не соотношение, полученное аналитическим путем. В результате трактовка соотношения оказывается не связанной с предпосылками и условностями, которые подразумевались при его выводе, и это является одной из причин тех парадоксов, которые связываются с данным соотношением. Конкретно, эти противоречия отметим в заключении нашего анализа. Приводим относительно простой вывод соотношения, делая упор на исходные постулаты и условности. 1. В основе соотношения лежит формула Планка, отражающая положение о квантовании “действия ”: E = n h или ее следствия:
Приращение “действия”, соответствующее h, D Sh = p D q или при одновременном изменении p и q: D Sh = D p D q. (2) 2. Отметим, что проявление импульса невозможно без перемещения, а проявление энергии — вне времени. Под “проявлением” подразумевается регистрация путем взаимодействия объекта с наблюдателем, с измерительным прибором. Это условие справедливо и в классической механике. 3. В случае использования соотношения неопределенности, а возможно и в общем случае, измеряется “действие”, а не его компоненты — импульс, координаты, энергию, время. Знаменательно — в действии объединены три основополагающие понятия: сила, длина, время. Измерительный же прибор “отградуирован”, соответственно, на импульс, координаты, энергию и время. 4. Неопределенность — это принципиальная невозможность определить величину параметра, а не результат влияния помех или ошибки измерения, подчиненных вероятностным законам, если их точное воздействие неизвестно. Неопределенность, которую нельзя устранить, имеет место и в классической механике, она просто объясняется и легко воспринимается. Это случай, когда ограничена разрешающая способность конкретного измерительного инструмента: слишком велика при измерении “цена деления”, т. е. измерение осуществляется с помощью определенного шаблона, а требуется точность более высокая, чем та, что обеспечивается размерами или другими параметрами шаблона. Ни у кого, например, не вызывает удивления, что величина разрешения, достигаемого микроскопом, ограничена длиной волны в луче освещения. Эта неопределенность не связана с нашим незнанием причины погрешности, тем более, что этой причины не существует — у нас нет методики или инструмента для более точного определения измеряемого параметра. 5. В соотношении неопределенность рассматривается как фактор, вызывающий ошибку. Следовательно, формально предполагается стремление получить большую точность, чем та, которая может обеспечить дискретная величина кванта действия. 78. Принципиальное отличие задания состояния частицы в квантовой и классической механике. Волновая функция и ее статистический смысл.
Состояние классической частицы в любой момент времени описывается заданием ее координат и импульсов (x,y,z,px,py,pz). Зная эти величины в момент времени t, можно определить эволюцию системы под действием известных сил во все последующие моменты времени. Координаты и импульсы частиц сами являются непосредственно на опыте измеряемыми величинами. В квантовой физике состояние системы описывается волновой функцией (x,y,z). Т.к. для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса и не имеет смысла говорить о движении частицы по определенной траектории, можно определить только вероятность нахождения частицы в данной точке в данный момент времени, которая связана с волновой функцией - > = H/ p, = - H/ t, где H - функция Гамильтона H = p2/2m + U(r), где U(r) - потенциал поля, в котором движется частица.
Поскольку из соотношения неопределенностей следует, что частица не имеет одновременно импульс и координату, то не следует об этом и говорить. А "говорить" следует о волновой функции, которая описывает микросостояние системы, ее волновые свойства. Де Бройль связал со свободно движущейся частицей плоскую волну. Известно,что плоская волна, распространяющаяся в направлении оси х описывается уравнением S=Acos(wt- kх+jО) или в экспоненциальной форме S=АOехр[i(wt- kх+jО)]. Заменив в соответствии с (1) и (2) w и k=2p/l через Е и p, уравнение волны де Бройля для свободной частицы пишут в виде Y =АOехр[(-i/ (в квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет |Y| 2, то это несущественно). Функцию Yназывают волновой функций или пси-функцией. Она, как правило, бывает комплексной. Интепретацию волновой функции дал в 1926 г. Борн: квадрат модуля волновой функции определяет вероятность того, что частица будет обнаружена в пределах объема dV: dP =|Y| 2 dV=YY*dV (17) где Y * - комплексно - сопряженная волновая функция. Величина |Y| 2=YY* = dP/ dV - имеет смысл плотности вероятности. Интеграл от (17), взятый по всему пространству, должен равняться единице (вероятность достоверного события Р=1).
Выражение (18) называют условием нормировки. Отметим еще раз, что волновая функция описывает микросостояние частицы, ее волновые свойства и она позволяет ответить на все вопросы, которые имеет смысл ставить. Например, найти энергию и импульс частицы. Для этого следует вычислить следующие частные производные Yпо координате х и времени t:
откуда
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 880; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.199 (0.012 с.) |


 )(Еt- pх)]. (16)
)(Еt- pх)]. (16)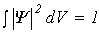 (18)
(18)




