
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая характеристика теории Максвелла для электромагнитного поля. Вихревое электрическое поле, первое уравнение Максвелла.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В 60-х годах прошлого столетия Д. К. Максвелл, основываясь на идеях Фарадея об электрическом и магнитном полях, обобщил законы, установленные экспериментальным путем, и разработал законченную теорию единого электромагнитного поля, создаваемого произвольной системой зарядов и токов. Теория Максвелла представляет собой феноменологическую теорию электромагнитного поля. Это означает, что внутренний механизм явлений, происходящих в среде и вызывающих появление электрических и магнитных полей, в теории не рассматривается. Теория Максвелла является макроскопической теорией электромагнитного поля. В ней рассматриваются электрические и магнитные поля, создаваемые макроскопическими зарядами и токами, т. е. зарядами, сосредоточенными в объемах, неизмеримо больших, чем объемы отдельных атомов и молекул. Кроме того, предполагается, что расстояния от источников полей до рассматриваемых точек пространства также во много раз больше размеров молекул. Поэтому заметные изменения полей, исследуемых в теории Максвелла, возможны только на протяжении расстояний, огромных по сравнению с размерами атомов и молекул. Наконец, периоды изменения переменных электрических и магнитных полей должны быть во много раз больше периодов внутримолекулярных процессов. В теории Максвелла рассматриваются усредненные электрическое и магнитное поля, причем усреднение соответствующих микрополей производится для интервалов времени, значительно больших периодов обращения или колебания элементарных зарядов, и для участков поля, объемы которых во много раз больше объемов атомов и молекул. ЭДС индукции, возбуждаемая в неподвижном замкнутом проводящем контуре, выражается формулой:
Тем самым было выяснено, что переменное магнитное поле создает в проводящем замкнутом контуре вихревое электрическое поле. Максвелл предложил считать, что соотношение (21.1) справедливо не только для проводящего, но и для любого замкнутого контура, мысленно выбранного в переменном магнитном поле. Иными словами, он предположил, что переменное магнитное поле создает в любой точке пространства вихревое электрическое поле независимо от того, находится в этой точке проводник или нет. Обобщенное таким образом равенство (21.1) называется первым уравнением Максвелла в интегральной форме: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру L равна взятой в обратным знаком скорости изменения магнитного потока сквозь поверхность, натянутую на контур. Уравнение Максвелла (21.1) можно также записать в форме
где направление обхода контура L и векторов dS согласовано между собой по правилу буравчика. 59. Ток смещения, второе уравнение Максвелла. Полная система уравнений Максвелла. Для количественной характеристики "магнитного действия" переменного электрического поля Максвелл ввел понятие тока смещения. Током смещения сквозь произвольную поверхность S называется физическая величина, численно равная потоку вектора плотности тока вмещения сквозь эту поверхность:
Максвелл обобщил закон полного тока, добавив в правую часть уравнения (21.11) ток смещения сквозь поверхность S, натянутую на замкнутый контур L:
Это равенство называется вторым уравнением Максвелла в интегральной форме. Оно показывает, что циркуляция вектора Н напряженности магнитного поля по произвольному замкнутому контуру L равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур. Полная система уравнений Максвелла имеет вид: I. II. III. IV.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.006 с.) |

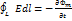 (21.1)
(21.1)









