
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные уравнения электродинамикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В основе макроскопической электродинамики лежат законы электромагнетизма, установленные опытным путем. Основными из них являются: 1) закон полного тока (закон Ампера); 2) закон индукции Фарадея; 3) закон Кулона; 4) свойство соленоидальности магнитного поля. Математическое обобщение этих законов дал известный английский физик Д.Максвелл (1820 - 1875). Он постулировал систему дифференциальных уравнений в частных производных, связывающих векторы электромагнитного поля с их источниками. Эти уравнения не вытекают из каких-либо других уравнений, а являются обобщением опытных данных, полученных при изучении электромагнитных явлений. Они являются фундаментальными соотношениями, из которых путем математических преобразований выводятся все остальные электромагнитные свойства изучаемых объектов. Первое уравнение Максвелла. Первое уравнение Максвелла является обобщением закона полного тока. Этот закон утверждает, что циркуляция вектора напряженности магнитного поля по замкнутому контуру в равна полному току I, пронизывающему данный контур (рис.1,a), т.е.
где
В правую часть соотношений (4), (5) входит только ток проводимости
Уравнение (6) носит название первого уравнения Максвелла. Оно утверждает, что переменное электрическое поле, так же как и ток проводимости, порождает магнитное поле, а силовые линии магнитного поля охватывают линии полного тока и связаны с ним правовинтовой системой (рис.1,а). Из уравнения (6) с учетом закона Кулона следует соотношение непрерывности для полного тока:
Выражение (7) соответствует формулировке дифференциальной формы закона сохранения заряда, который утверждает, что всякому изменению заряда в некоторой области соответствует электрический ток, вытекающий или втекающий в данную область. Интегральная форма этого закона получается после интегрирования (7) по области
Второе уравнение Максвелла. Второе уравнение Максвелла является обобщением закона индукции Фарадея, который был сформулирован только для проводящих контуров и связывает ЭДС, наведенную в контуре, со скоростью изменения магнитного потока, пронизывающего этот контур
Выражения (8) и (9) носят название второго уравнения Максвелла в интегральной и дифференциальной форме соответственно. Эти уравнения связывают циркуляцию вектора электрического поля по замкнутому контуру Третье уравнение Максвелла. Это уравнение является обобщением закона Кулона на случай произвольных переменных полей. В интегральной и дифференциальной форме соответственно это уравнение имеет следующий вид:
Уравнение (10) связывает поток вектора электрической индукции Четвертое уравнение Максвелла. Четвертое уравнение Максвелла в интегральной форме записывается
Это выражение совпадает с законом Гаусса для магнитного поля, который утверждает, что силовые линии магнитного поля всегда замкнуты и не имеют истоков и стоков. Поэтому всегда поток вектора Дифференциальная форма этого уравнения имеет вид
Уравнения (12), (13) отражают тот опытный факт, что силовые линии магнитного поля всегда непрерывны и замкнуты, в природе отсутствуют магнитные заряды, а существуют только магнитные диполи. Магнитное поле всегда соленоидальное. Сторонние источники, полная система уравнений Максвелла. Возникновение любого электромагнитного поля в определенной области всегда обязано какой-то первопричине - источникам, вызвавшим его появление. Такими источниками могут быть токи
Эту систему дополняют тремя материальными уравнениями, характеризующими параметры среды:
Если среды в рассматриваемой, области линейные, то и уравнения (14), (15) тоже линейные, и к их решению применим принцип суперпозиции. Система уравнений (11), (12) отражает неразрывную связь электрических и магнитных явлений: изменение одного поля непременно вызывает изменение другого; источниками электромагнитного поля всегда являются электрические заряды; магнитное поле всегда вихревое и его линии схватывают линии полного тока. Классификация электромагнитных явлений. В уравнения Максвелла входят производные по времени от электромагнитных величин. В связи с этим принято классифицировать электромагнитные явления по скорости изменения процесса следующим образом. Выделяют: 1) статическое поле; 2) поле постоянного тока; 3) медленно меняющееся по времени поле - квазистационарное поле; 4) электродинамическое быстропеременное поле (монохроматическое). В каждом из этих случаев система уравнений Максвелла упрощается из-за отсутствия тех или иных членов. 1. Наиболее простыми из электромагнитных явлений являются статические поля. Для них очевидно Система уравнений Максвелла для этих полей распадается на две независимые системы уравнений:
Первая из них описывает электростатическое поле - поле неподвижных электрических зарядов. В нее входят только электрические величины и диэлектрические параметры среды. Вторая система характеризует магнитостатическое поле -поле постоянных магнитов. Таким образом, делание системы уравнений Максвелла на две независимые системы показывает, что статические магнитные и электрические пола существуют независимо друг от друга. 2. Поле постоянного тока называется стационарным электромагнитным полем. Для него
Таким образом, уравнения Максвелла для поля постоянного тока представляют собой единую систему. 3. Квазистационарные процессы имеют место, если 4. Монохроматическое электромагнитное поле - это поле, для которого зависимость от времени может быть выражена множителем
Л е к ц и я 3 Электростатическое поле
Решение задач, связанных с определением ряда параметров СВЧ устройств, таких, как электрическая прочность, допустимая мощность передачи, распределенная емкость многосвязанных линий передач и других, осуществляют в электростатическом приближении. Электростатическое поле - это поле неподвижных зарядов, оно является потенциальным. Потенциальность этого поля следует из соотношения
Здесь потенциал Разность потенциалов двух точек
где Как следует из выше приведенных соотношений, разность потенциалов и работа сил поля в электростатическом поле не зависит от пути интегрирования, а зависит только от положения начальной и конечной точек. Из третьего уравнения Максвелла и соотношения (16) следует, что для области, содержащей источники, потенциал удовлетворяет уравнению Пуассона
то уравнение Пуассона переходит в уравнение Лапласа Решение уравнения Пуассона в случае зарядов, распределенных в объеме с плотностью
В электростатическом поле вводят понятие эквипотенциальных поверхностей - поверхностей равного потенциала Покажем, что в средах с конечной проводимостью
Таким образом, можно утверждать, что в среде с конечной проводимостью
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.01 с.) |

 , (4)
, (4) - поверхность, опирающаяся на замкнутый контур
- поверхность, опирающаяся на замкнутый контур  . Дифференциальная форма соотношения (4) получается с помощью теоремы Стокса и имеет вид
. Дифференциальная форма соотношения (4) получается с помощью теоремы Стокса и имеет вид , (5)
, (5) , поэтому закон Ампера справедлив только для цепи постоянного тока, а для цепи переменного тока, например, содержащей конденсатор, в котором нет тока проводимости, он нарушается. Д.Максвелл распространил этот закон на случай переменных полей. Для этого он предположил, что переменное электрическое поле в отсутствии свободных зарядов так же порождает магнитное поле, как и ток проводимости. На этом основании он ввел в правую часть соотношения (4) и (5) добавочный член - ток смещения
, поэтому закон Ампера справедлив только для цепи постоянного тока, а для цепи переменного тока, например, содержащей конденсатор, в котором нет тока проводимости, он нарушается. Д.Максвелл распространил этот закон на случай переменных полей. Для этого он предположил, что переменное электрическое поле в отсутствии свободных зарядов так же порождает магнитное поле, как и ток проводимости. На этом основании он ввел в правую часть соотношения (4) и (5) добавочный член - ток смещения  - характеризующий переменное электрическое поле;
- характеризующий переменное электрическое поле; ,(6)
,(6) , (7)
, (7) :
: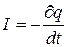
 . Максвелл распространил этот закон на произвольный замкнутый контур и записал его в виде следующие уравнений:
. Максвелл распространил этот закон на произвольный замкнутый контур и записал его в виде следующие уравнений: , (8)
, (8) , (9)
, (9) через произвольную поверхность S, опирающуюся на контур
через произвольную поверхность S, опирающуюся на контур 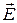 препятствует изменению вектора
препятствует изменению вектора  , (10)
, (10) , (11)
, (11) через произвольную замкнутую поверхность S с полным зарядом
через произвольную замкнутую поверхность S с полным зарядом  заключенным в объеме V, ограниченном этой поверхностью. Уравнение (11) соответственно характеризует источники электрического поля в каждой точке пространства.
заключенным в объеме V, ограниченном этой поверхностью. Уравнение (11) соответственно характеризует источники электрического поля в каждой точке пространства. , (12)
, (12) , (13)
, (13)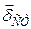 , заряды
, заряды  или поля
или поля  . Эти источники обычно считаются заданными и входят в правую часть уравнений Максвелла в виде отдельных слагаемых. Полная система уравнений Максвелла со сторонними токами и зарядами имеет вид
. Эти источники обычно считаются заданными и входят в правую часть уравнений Максвелла в виде отдельных слагаемых. Полная система уравнений Максвелла со сторонними токами и зарядами имеет вид , (14)
, (14)
 ,
,  ,
,  (15)
(15) и
и  .
.


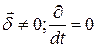 и между электрическим и магнитным полем имеется строгая связь, выраженная законом Ома (3) и законом полного тока (5):
и между электрическим и магнитным полем имеется строгая связь, выраженная законом Ома (3) и законом полного тока (5):
 и в первом уравнении Максвелла можно пренебречь током смещения.
и в первом уравнении Максвелла можно пренебречь током смещения. . Это позволяет, применив метод комплексных амплитуд, избавиться от операций дифференцирования и интегрирования по времени, заменив их соответственно умножением или делением на
. Это позволяет, применив метод комплексных амплитуд, избавиться от операций дифференцирования и интегрирования по времени, заменив их соответственно умножением или делением на  .При этом запись системы уравнений Максвелла значительно упрощается.
.При этом запись системы уравнений Максвелла значительно упрощается. , которое позволяет представить вектор
, которое позволяет представить вектор 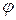 :
: , (16)
, (16) определяется как работа, совершаемая против сил поля, при перемещении положительного единичного заряда от одной точки к другой:
определяется как работа, совершаемая против сил поля, при перемещении положительного единичного заряда от одной точки к другой:

 или
или  , где в декартовой системе координат
, где в декартовой системе координат . Если в рассматриваемой области заряды отсутствуют,
. Если в рассматриваемой области заряды отсутствуют,
 имеет вид
имеет вид  . Для точечного заряда значение потенциала
. Для точечного заряда значение потенциала 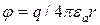
 . Эти поверхности, как следует из выражения (16), ортогональны силовым линиям электрического поля.
. Эти поверхности, как следует из выражения (16), ортогональны силовым линиям электрического поля. отсутствует электростатическое поле и не может быть постоянного объемного заряда. Для этого уравнение непрерывности
отсутствует электростатическое поле и не может быть постоянного объемного заряда. Для этого уравнение непрерывности  преобразуем на основании закона Ома
преобразуем на основании закона Ома 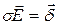 и третьего уравнения Максвелла
и третьего уравнения Максвелла  в однородное дифференциальное уравнение относительно объемной плотности заряда:
в однородное дифференциальное уравнение относительно объемной плотности заряда:
 Решение этого уравнения
Решение этого уравнения  показывает (рис. 2), что объемная плотность заряда
показывает (рис. 2), что объемная плотность заряда  . Величина
. Величина  называется временем релаксации, оно равно времени, за которое плотность заряда убывает в
называется временем релаксации, оно равно времени, за которое плотность заряда убывает в  раз.
раз. и, следовательно, в таких средах не может существовать электростатического поля
и, следовательно, в таких средах не может существовать электростатического поля 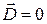 . Поэтому на основания (16) можно утверждать, что если в проводящих средах
. Поэтому на основания (16) можно утверждать, что если в проводящих средах  ,то для них
,то для них 


