
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волновод прямоугольного сеченияСодержание книги Поиск на нашем сайте
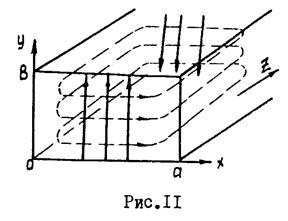
Наибольшее распространение в сантиметровом и миллиметровом диапазонах волн получили волноводы прямоугольного и круглого сечений. Эти линии передачи являются односвязанными системами, поэтому в них могут существовать волны с продольными составляющими поля. Для прямоугольных волноводов принято следующее стандартное обозначение геометрических размеров (рис. 11): широкая стенка - а, узкая стенка - в.
при следующих граничных условиях:
Его решение
где
а т и n независимо друг от друга принимают целые значения 0, 1, 2... Каждому значению т и п соответствует свой тип волны, который обозначается Нтп. Значения m и n определяют число стоячих полуволн поля, укладывающихся соответственно вдоль поперечных координат Х и Y. Равенство индекса т или n нулю означает, что поле вдоль соответствующей поперечной координаты по амплитуде не изменяется. Из сказанного следует, что значение 0 эти индексы одновременно принимать не могут, так как при этом согласно граничным условиям исчезают поперечные составляющие полей
Поэтому сигнал одной и той же частоты, распространяясь в волноводе посредством различных типов волн, будет иметь различные параметры: Значения поперечных составляющих поля волны Нтп находятся из уравнений связи между продольными и поперечными составляющими по известному значении
По стенкам волновода протекают электрические тока, которые определяются из граничных условий Волны Е-типа. Параметры этих волн находят из решения волнового уравнения для продольной составляющей электрического поля при граничных условиях
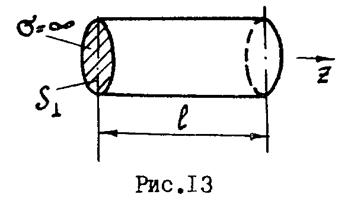
Поперечное волновое число Из сказанного следует, что
Волноводы круглого сечения
Геометрия поперечного сечения круглого волновода показана на рис. 12. Решение волнового уравнения для этих волноводов проводят в цилиндрической системе координат с переменными
Здесь т характеризует число полных периодов изменения поля по координате
На основании этого уравнения из решения (65) получим уравнение для определения поперечного волнового числа Таким образом, поперечное волновое число находится как п -йкорень производной функции Бесселя первого рода m -го порядка:
Для круглого волновода основной волной является волна H11, а ее ближайший высший тип - волна Е01:
Для Е и Н типов волн в круглом волноводе индекс т может принимать значение нуль, а n - всегда больше нуля. Структура поля волны H11 показана на рис. 12.
Лекция 9 Объемные резонаторы
Объемные резонаторы относятся к одним из наиболее распространенных избирательных элементов СВЧ диапазона. В отличие от низкочастотных избирательных LC -контуров в СВЧ диапазоне такие устройства реализуются в системах с распределенными параметрами. Возможность построения таких систем вытекает из уравнений Максвелла, согласно которым изменение электрического поля 1) резонансная длина волны 2) активная проводимость 3) собственная или ненагруженная добротность Параметры Резонансная длина волны. Рассмотрим условие существования электромагнитного поля в отрезке регулярной направляющей системы длиной
Отсюда из (66) на основании граничных условий (25) при определена следующим образом:
Очевидно, на основании (I) для волн типов Т и Н, укоторых полное электрическое поле Тип волны в резонаторе обозначается тремя индексами: т, n, p. Первые два определяют структуру поля в поперечном сечении, третий - характеризует поле стоячей волны в продольном сечении резонатора, например: Активная проводимость резонатора. Эта характеристика является мерой активных потерь в резонаторе и ее определяют как
где Рп - мощность активных потерь в резонаторе; Um- напряжение на входных клеммах резонатора. Так как для полых резонаторов нет однозначного определения величины напряжения Um, то понятие G является неопределенным. Обычно Um определяют как
Из выражения (67) следует, что мощность активных потерь и, следовательно, активная проводимость резонатора зависит от качества материала, его обработки и от структуры поля. Добротность резонатора. Для определения добротности резонаторов используют известное энергетическое соотношение для средних за период величин:
где Тк - период колебания;
В момент фазы колебания, когда
Значение собственной добротности с учетом (67) и (68) будет
где в выражениях (67) и (68) учтено, что для немагнитных материалов При заполнении объемного резонатора диэлектриком с потерями
а запасенная энергия На практике часто используют выражение добротности резонатора через значение активной и реактивной проводимости G, В на его входных клеммах. Для этого по аналогии с контурами запасенную энергию, мощность потерь в резонаторе и его добротность представляют как
Значение емкости С для систем с распределенными параметрами однозначно не определяется, поэтому ее выражают через входную реактивную проводимость b. Полная входная реактивная проводимость для контуров вблизи резонанса имеет вид:
где учтено, что
Соотношение (71) характеризует добротность резонатора вблизи резонансной частоты. Нагруженная и внешняя добротность резонатора. Если резонатор подключен к полезной нагрузке, то полная энергия потерь будет
где
Соответственно величина добротности через эквивалентные проводимости по аналогии с (71) примет вид:
Нагруженная добротность зависит от величины связи резонатора с нагрузкой и от его собственной добротности.
Лекция 10 Элементы теории цепей
Любой СВЧ тракт радиотехнической системы выключает в себя самые разнообразные неоднородности и элементы, которые, в конечном счете, и определяют его характеристики. Строго говоря, когда размеры этих элементов соизмеримы с длиной волны, то их расчет нужно вести методами электродинамики. Однако это сложный и неоптимальный путь. Для упрощения решения подобных задач сложную волноводную систему приводят к некоторой эквивалентной схеме, состоящей из отрезков регулярных линий и сопротивлений, а СВЧ узел рассматривают как некоторый многополюсник. Такое представление СВЧ узлов приводит к простым соотношениям между входными и выходными параметрами, и к их анализу применим математический аппарат матричной алгебры, хорошо разработанный в теории цепей. В отличие от низкочастотных цепей на СВЧ для этого метода анализа появляется ряд особенностей: 1. Нужно учитывать волновой характер процессов, что требует фиксации клеммных плоскостей, определяющих фазу процесса и длину соединяющих отрезков линий. 2. Имеется возможность распространения многих типов волн: Т, Е, Н. Если устройство допускает существование нескольких типов волн, то на выходах многополюсника каждому типу волны должна соответствовать своя пара клемм. 3. На клеммах многополюсников, соединяемых между собой, должны быть одинаковые типы волн, а преобразование типа волны должно происходить внутри многополюсника. Каждый узел представляется как некоторый многополюсник с n выходами и 2п клеммами. Если многополюсник представляет линейную цепь, то он описывается линейными алгебраическими уравнениями. На практике получили распространение два вида уравнений. В первом из них описывается связь между напряжением U и током I на клеммах посредством импедансных матриц: матрицы сопротивлений Двухполюсные системы СВЧ. Простейшими многополюсниками являются двухполюсные системы. Это схемы с одной парой клемм (рис. 14). Все свойства данной схемы характеризуются входным сопротивлением
Импедансные матрицы четырехполюсников. Связь между напряжениями и токами на выходах четырехполюсника может быть выражена шестью различными способами (рис.15).Наиболее употребительные из них три: это матрицы сопротивлений проводимости и передачи:
Система (74) характеризуется матрицей сопротивлений:
Физический смысл элементов матрицы Для взаимного четырехполюсника Вторая система (73) характеризуется матрицей проводимости Третья система (74) характеризуется матрицей передачи
Для произвольного многополюсника вводят следующие обозначения (рис. 16): падающую (входящую) волну в i -м плече обозначают через
.....
или, используя матричную запись, систему (76) запишем:
где
Физический смысл элементов матрицы есть коэффициент передачи из плеча k - в плечо i; Итак, элементы матрицы Матрица Многополюсники без потерь. При анализе большинства СВЧ узлов можно пренебречь потерями, т.е. считать, что потеря в устройстве отсутствуют и энергия падающих волн равна энергии отраженных волн. Для них матрица рассеяния обладает свойством унитарности, т.е.
где [1] - единичная матрица. Для взаимных многополюсников
при
Физический смысл соотношения (79) составляет условие баланса мощности в многополюснике без потерь, т.е. если р -му плечу подводится единичная мощность, то каждый из квадратов модулей элементов Соотношение (79) для многополюсника без потерь часто используют для проверки практических расчетов сложных СВЧ узлов.
Литература 1. Семенов Н.А. Техническая электродинамяка.м.,"Связь" 1973. 2. Красюк Н.П., Димович Н.0. Электродинамика и распространение радиоволн. М., "Высшая школа", 1974. 3. Фальковский О.И. Техническая электродинамика. М., "Связь", 1978. 4. Гольдштеин Л.О., 3ернов Н, Б. Электромагнитные поля и волны в современной радиотехнике. М.,"Связь",1950. 5. Никольский В.В. Теория электромагнитного поля. М., "Высшая школа", 1964.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1032; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.99.221 (0.01 с.) |

 Структура полей и параметры волн Н или Е - типов в волноводе определяются из решения однородного волнового уравнения соответственно для
Структура полей и параметры волн Н или Е - типов в волноводе определяются из решения однородного волнового уравнения соответственно для  или
или  , составляющих поля с граничными условиями для идеально проводящих стенок. Волны Н -типа. Параметры этих волн определяются из волнового уравнения (47) для составляющей и соотношений (52)
, составляющих поля с граничными условиями для идеально проводящих стенок. Волны Н -типа. Параметры этих волн определяются из волнового уравнения (47) для составляющей и соотношений (52)

 ;
; 
 .
. ; ( 62 )
; ( 62 ) ; (63)
; (63) и
и 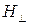 . Каждому типу волна Нтп соответствует свое значение поперечного волнового числа
. Каждому типу волна Нтп соответствует свое значение поперечного волнового числа  и следовательно,
и следовательно,  :
: ; (64)
; (64)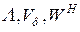 и т.д. Тип волны в волноводе, для которого значение
и т.д. Тип волны в волноводе, для которого значение  , основным типом волны является волна
, основным типом волны является волна  . Основной тип волны имеет наибольшее практическое значение, он характеризуется минимальными потерями и минимальными поперечными размерами волновода. Для него существует в определенном диапазоне частот
. Основной тип волны имеет наибольшее практическое значение, он характеризуется минимальными потерями и минимальными поперечными размерами волновода. Для него существует в определенном диапазоне частот  одномодовый режим работы, когда в волноводе другие типы колебаний, кроме основного, не существуют. Здесь
одномодовый режим работы, когда в волноводе другие типы колебаний, кроме основного, не существуют. Здесь  - критическая частота ближайшего высшего типа колебания.
- критическая частота ближайшего высшего типа колебания. при m=1, n=0 имеем только три составляющие поля
при m=1, n=0 имеем только три составляющие поля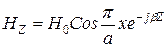 ;
;  ;
; ;
; 
 . Линии этих токов образуют с магнитным полем, касательным к стенкам волновода, ортогональную сетку (рис. 11).
. Линии этих токов образуют с магнитным полем, касательным к стенкам волновода, ортогональную сетку (рис. 11). . Это решение имеет вид, аналогичный (3):
. Это решение имеет вид, аналогичный (3):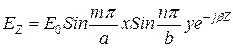
 . Волны, для которых критические частоты совпадают, называются вырожденными волнами, поскольку все основные параметры этих волн совпадают и становятся трудно различимыми.
. Волны, для которых критические частоты совпадают, называются вырожденными волнами, поскольку все основные параметры этих волн совпадают и становятся трудно различимыми. и
и 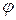 при граничных условиях на стенках
при граничных условиях на стенках 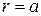 , Для электрических и магнитных волн решение этого уравнения имеет вид
, Для электрических и магнитных волн решение этого уравнения имеет вид (65)
(65) где
где 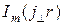 -функция Бесселя первого рода т- гопорядка аргумента
-функция Бесселя первого рода т- гопорядка аргумента  ,
,  . Значение поперечного волнового числа
. Значение поперечного волнового числа  и из (65) следует, что
и из (65) следует, что  т.е. аргумент функция Бесселя при
т.е. аргумент функция Бесселя при  и значит:
и значит: ;
; 
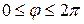 ; п - изменение поля вдоль радиуса или число полюсов функции
; п - изменение поля вдоль радиуса или число полюсов функции 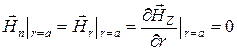
 .
. ;
; 
 ;
; 
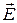 вызывает появление магнитного поля
вызывает появление магнитного поля  . Такой обмен энергиями этих полей происходит в любой точке пространства. Из уравнения энергетического баланса (26), (27) следует, что если в замкнутой области отсутствуют тепловые потери, потери на излучение, то этот обмен может происходить сколь угодно долго. Поэтому свойствами колебательной системы обладает любая изолированная система, ограниченная отражающей оболочкой. Основными параметрами резонаторов на СВЧ, в отличие от колебательных контуров с сосредоточенными параметрами, которые характеризуются L, С, R, являются:
. Такой обмен энергиями этих полей происходит в любой точке пространства. Из уравнения энергетического баланса (26), (27) следует, что если в замкнутой области отсутствуют тепловые потери, потери на излучение, то этот обмен может происходить сколь угодно долго. Поэтому свойствами колебательной системы обладает любая изолированная система, ограниченная отражающей оболочкой. Основными параметрами резонаторов на СВЧ, в отличие от колебательных контуров с сосредоточенными параметрами, которые характеризуются L, С, R, являются: , или частота fo;
, или частота fo; - мера активных потерь;
- мера активных потерь;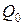 .
. ,
,  закороченной по концам при
закороченной по концам при  и
и  идеально проводящей металлической стенкой
идеально проводящей металлической стенкой  (рис. 13). Граничное условие (25) для поперечной составляющей электрического поля на стенках
(рис. 13). Граничное условие (25) для поперечной составляющей электрического поля на стенках  будет
будет  при
при  (66)
(66) , а условие при
, а условие при  , т.е.
, т.е.  . Значит, длина замкнутой направляющей системы должна быть кратной целому числу длин полуволн
. Значит, длина замкнутой направляющей системы должна быть кратной целому числу длин полуволн  где
где  . Выражение (66) показывает, что фаза поля в колебательной системе неизменна и поле носит характер стоячей волны. Резонансная частота и резонансная длина волны для резонатора длиной
. Выражение (66) показывает, что фаза поля в колебательной системе неизменна и поле носит характер стоячей волны. Резонансная частота и резонансная длина волны для резонатора длиной 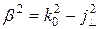 ;
; 

 ,
,  значение нуль принимать не может. Для волн типа Е равенство
значение нуль принимать не может. Для волн типа Е равенство  , а длина резонатора при
, а длина резонатора при  является неопределенной.
является неопределенной. ;
;  .
.
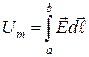 между характерными точками резонатора (а и b), например, на входных клеммах. Если допустить, что потери в резонаторе имеют место только в металлических стенках
между характерными точками резонатора (а и b), например, на входных клеммах. Если допустить, что потери в резонаторе имеют место только в металлических стенках  с поверхностным сопротивлением
с поверхностным сопротивлением  , то величину потерь в резонаторе
, то величину потерь в резонаторе  можно оценить следующим образом:
можно оценить следующим образом: (67)
(67)
 - резонансная частота;
- резонансная частота; - запасенная электромагнитная энергия.
- запасенная электромагнитная энергия.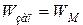 , запасенная энергия может быть подсчитана:
, запасенная энергия может быть подсчитана: (68)
(68) (69)
(69)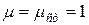 . Если пренебречь вариацией поля в резонаторе и полагать, что
. Если пренебречь вариацией поля в резонаторе и полагать, что  , то выражение (69) значительно упростится:
, то выражение (69) значительно упростится:  , где учтено, что
, где учтено, что  ,
,  , т.е. добротность резонатора пропорциональна отношению
, т.е. добротность резонатора пропорциональна отношению  .
. мощность потерь в диэлектрике определяется:
мощность потерь в диэлектрике определяется:
 . Добротность в диэлектрике будет
. Добротность в диэлектрике будет  , а при наличии магнитных потерь
, а при наличии магнитных потерь  .
. ;
; 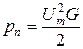 ;
;  (70)
(70)
 . Вблизи резонанса при
. Вблизи резонанса при 
 ,и выражение для реактивной проводимости b будет
,и выражение для реактивной проводимости b будет  , откуда
, откуда  . Отсюда выражение (70) для добротности может быть записано как
. Отсюда выражение (70) для добротности может быть записано как (71)
(71) , а добротность резонатора с нагрузкой характеризуется нагруженной добротностью
, а добротность резонатора с нагрузкой характеризуется нагруженной добротностью
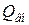 - внешняя добротность резонатора - определяется, величиной нагрузки
- внешняя добротность резонатора - определяется, величиной нагрузки


 , матрицы проводимостей
, матрицы проводимостей  и матрицы передачи
и матрицы передачи  . Во втором - используются соотношения между падающими и отраженными волнами. Их связывают волновые матрицы:
. Во втором - используются соотношения между падающими и отраженными волнами. Их связывают волновые матрицы:  - матрица рассеяния и
- матрица рассеяния и  - волновая матрица передачи.
- волновая матрица передачи. , или коэффициентом отражения Г:
, или коэффициентом отражения Г: ;
; 
 Большое значение в СВЧ устройствах имеют реактивные двухполюсники (короткозамыкатели, шлейфы, резонаторы и др.). Эти двухполюсники обладают рядом общих свойств, сформулированных в теореме Фостера. Если в двухполюснике нет активных потерь, то его сопротивление на входе чисто реактивное
Большое значение в СВЧ устройствах имеют реактивные двухполюсники (короткозамыкатели, шлейфы, резонаторы и др.). Эти двухполюсники обладают рядом общих свойств, сформулированных в теореме Фостера. Если в двухполюснике нет активных потерь, то его сопротивление на входе чисто реактивное  ;
;  ,причем
,причем  ;
;  . В отличие от низкочастотных цепей двухполюсные реактивные СВЧ устройства являются многорезонансными, так как для них резонансы имеют место на всех кратных частотах.
. В отличие от низкочастотных цепей двухполюсные реактивные СВЧ устройства являются многорезонансными, так как для них резонансы имеют место на всех кратных частотах.
 ; (72)
; (72) ; (73)
; (73) (74)
(74) ;
; ; (75)
; (75)
 . Так из (75) следует, что при
. Так из (75) следует, что при 
 - входное сопротивление при разомкнутом выходе; при
- входное сопротивление при разомкнутом выходе; при 
 -выходное сопротивление; при
-выходное сопротивление; при 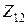
 переходные сопротивления соответственно.
переходные сопротивления соответственно. , для симметричного -
, для симметричного -  . Симметричный и взаимный четырехполюсник характеризуются двумя элементами матрицы:
. Симметричный и взаимный четырехполюсник характеризуются двумя элементами матрицы:  . Матрицу сопротивлений целесообразно использовать при последовательном соединении четырехполюсников, так как для них суммарная матрица
. Матрицу сопротивлений целесообразно использовать при последовательном соединении четырехполюсников, так как для них суммарная матрица  есть сумма отдельных
есть сумма отдельных  .
. .
. Волновые матрицы многополюсников. В уравнения (72)- (74) с импедансными матрицами входят интегральные величины: напряжения
Волновые матрицы многополюсников. В уравнения (72)- (74) с импедансными матрицами входят интегральные величины: напряжения 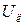 и ток
и ток  . Эти величины могут быть представлены в виде суммы падающих и отраженных волн. В СВЧ диапазоне измерение интегральных величин сложно, и обычно измеряют частоту
. Эти величины могут быть представлены в виде суммы падающих и отраженных волн. В СВЧ диапазоне измерение интегральных величин сложно, и обычно измеряют частоту  , мощность Р, КСВ или модуль и фазу коэффициента отражения. Измерение КСВ и коэффициента отражения непосредственно связано с измерением падающей и отраженной волны. Поэтому уравнения, связывающие падающие и отраженные волны многополюсника в СВЧ диапазоне, более наглядны и позволяют просто сопоставить результаты эксперимента.
, мощность Р, КСВ или модуль и фазу коэффициента отражения. Измерение КСВ и коэффициента отражения непосредственно связано с измерением падающей и отраженной волны. Поэтому уравнения, связывающие падающие и отраженные волны многополюсника в СВЧ диапазоне, более наглядны и позволяют просто сопоставить результаты эксперимента. , аотраженную или выходящую - через
, аотраженную или выходящую - через  . Пассивный линейный п -полюсник может быть описан системой п линейных алгебраических уравнений относительно волн
. Пассивный линейный п -полюсник может быть описан системой п линейных алгебраических уравнений относительно волн  ;
;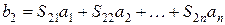 ; (76)
; (76) ;
;
 ; (77)
; (77) ,и из (5) получим
,и из (5) получим  ;
;  ;
;  . Отсюда можно сказать, что
. Отсюда можно сказать, что  при
при 
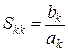 - коэффициент отражения от k -го плеча при условии полного согласования всех плеч многополюсника.
- коэффициент отражения от k -го плеча при условии полного согласования всех плеч многополюсника. - коэффициенты отражения от i -го входа при полном согласовании остальных плеч.
- коэффициенты отражения от i -го входа при полном согласовании остальных плеч.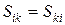 , поэтому
, поэтому  , где
, где  - транспонированная патрица (это матрица, у которой строки заменены столбцами).
- транспонированная патрица (это матрица, у которой строки заменены столбцами). (78)
(78) .Условие (78) означает, что
.Условие (78) означает, что



 (79)
(79) является долей мощности, выделяющейся в согласованной нагрузке k -го плеча, а
является долей мощности, выделяющейся в согласованной нагрузке k -го плеча, а  - доля отраженной мощности от плеча р,
- доля отраженной мощности от плеча р,


