
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физические характеристики электромагнитного поля и его источниковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Элементы теории электромагнитного поля Лекция 1 Предметом изучения данного курса является теория конструирования и расчета элементов и узлов радиоэлектронной аппаратуры СВЧ, а также вопросы их технологии и производства. Определяя СВЧ диапазон, можно сказать, что он охватывает область частот от 30 МГц до 3000 МГц. Этот диапазон разбивается на поддиапазоны.
Характерным для этой области частот является то, что длина волны электромагнитного сигнала, как правило, соизмерима или во много раз меньше размеров изучаемого объекта. Это определяет принципиальные конструктивные отличия высокочастотных элементов радиоэлектронной аппаратуры и отличает физику их работы от аналогичных низкочастотных устройств. Так, в СВЧ диапазоне: 1) теряют физический смысл обычные элементы с сосредоточенными параметрами L, C, R, а все СВЧ устройства являются устройствами с распределенными параметрами; 2) конструкции линий передач строго определяются физическими процессами передачи СВЧ энергии и имеют свои особенности для каждого диапазона частот; 3) электрические токи протекают всегда в очень тонком наружном слое металлических проводников, измеряемом в долях микрон (эта особенность накладывает жесткие требования на чистоту обработки токонесущих поверхностей, на выбор защитных покрытий и т.д.) 4) из-за большой инерции электронов и большой длительности рекомбинации свободных носителей в СВЧ диапазоне неприменимы обычные электровакуумные полупроводниковые приборы. Перед конструктором обычно ставится задача не только обеспечить требуемые характеристики устройств, но и обеспечить его работоспособность при воздействии внешних возмущающих факторов. При этом надо учесть, что многие СВЧ узлы, такие, как антенна и прилегающие к ней элементы, являются наружными устройствами, работающими обычно под влиянием сложного комплекса физических и химических воздействий. Рассмотрим на примере бортовой аппаратуры летательного аппарата некоторые из этих факторов. 1. Аэродинамический или кинетический нагрев вызывает линейное изменение размеров устройства, что приводит к искажению его частотных характеристик. Устранить такое влияние температуры удается специальными конструктивными приемами и подбором соответствующих материалов. С нагревом возникает термическая ионизация среды, в результате сильно ухудшаются характеристики излучения антенн. 2. Сильные вибрации и ударные нагрузки накладывают требования прочности, жесткой взаимной связи элементов конструкции. 3. Скоростной напор и современная аэродинамика аппаратов требует применения невыступающих внешних устройств СВЧ. 4. В условиях разряженной атмосферы сильно снижается электрическая прочность устройств. Так, на высоте 30 км, где давление атмосферы составляет приблизительно 18 мм рт.ст., электрическая прочность узлов СВЧ падает в 10 раз. 5. На космических объектах серьезным фактором является эрозия поверхности металлов и диэлектриков. Кроме того, всегда имеет место химическое воздействие влажности, пыли, что требует применения специальных защитных мер (выбор защитных покрытий, материалов герметизации и др.). Таким образом, при конструировании СВЧ устройств приходится считаться с весьма противоречивыми требованиями. Например, с одной стороны - минимальный вес, минимальные размеры, стабильность характеристик, высокий КПД, минимальная стоимость, с другой стороны - механическая прочность, электрическая прочность, теплостойкость, устойчивость к химическим воздействиям. Удовлетворить всем этим требованиям удается только в результате правильного выбора типа устройства, его конструкции, соответствующего подбора материалов и методов их обработки. Принцип работы всех устройств СВЧ основан на взаимодействии высокочастотного электромагнитного поля со средой и ее границами, образующими данное устройство. Физика этого взаимодействия описывается законами электродинамики, в основе которых лежит классическая или максвелловская теория электромагнитного поля, учитывающая только микроскопические свойства вещества и не затрагивающая процессы, происходящие на атомарном уровне.
Лекция 2 Л е к ц и я 3 Электростатическое поле
Решение задач, связанных с определением ряда параметров СВЧ устройств, таких, как электрическая прочность, допустимая мощность передачи, распределенная емкость многосвязанных линий передач и других, осуществляют в электростатическом приближении. Электростатическое поле - это поле неподвижных зарядов, оно является потенциальным. Потенциальность этого поля следует из соотношения
Здесь потенциал Разность потенциалов двух точек
где Как следует из выше приведенных соотношений, разность потенциалов и работа сил поля в электростатическом поле не зависит от пути интегрирования, а зависит только от положения начальной и конечной точек. Из третьего уравнения Максвелла и соотношения (16) следует, что для области, содержащей источники, потенциал удовлетворяет уравнению Пуассона
то уравнение Пуассона переходит в уравнение Лапласа Решение уравнения Пуассона в случае зарядов, распределенных в объеме с плотностью
В электростатическом поле вводят понятие эквипотенциальных поверхностей - поверхностей равного потенциала Покажем, что в средах с конечной проводимостью
Таким образом, можно утверждать, что в среде с конечной проводимостью
Л е к ц и я 4 Лекция 6 Линии передачи СВЧ диапазона Направляющие системы, или линии передачи, предназначены для передачи электромагнитной энергии. Существует много типов направляющих систем, каждая из которых применяется в определенной области техники СВЧ и в определенном диапазоне частот. Ниже будут рассмотрены линии передачи, которые по всем своим параметрам не имеют зависимости по продольной координате Z и имеют однородное заполнение. Такие линии называются регулярными и однородными. Их классификацию проводят следующим образом.
2. Линии полуоткрытого типа это линии, не имеющие полной экранировки от соседних линий передачи и внешнего пространства. К ним относятся различные полосковые линии передачи (рис. 4, г, д). 3. Линии открытого типа - это линии, не имеющие экранировки от внешнего пространства. К ним относятся двухпроводные линии, диэлектрические Рис. 4 волноводы и др. (рис. 4, е, ж). Основные технические требования к направляющим системам сводятся к следующему: минимальное затухание на единицу длины линии, максимальная экранировка или помехозащищенность, диапазонность, максимум допустимой мощности передачи. Конструкция линии должна обладать минимальными размерами, весом, стоимостью. Характерным для всех линий передач СВЧ диапазона является то, что в зависимости от их поперечного сечения электромагнитное поле в них может распространяться в виде бесконечно большого числа типов колебаний (типов волн), отличающихся друг от друга структурой поля. Параметры этих типов колебаний находятся из решения однородного волнового уравнения Гельмгольца с учетом граничных условий на стенках линии передачи. В общем случае в отличии от плоской волны в свободном пространстве электромагнитное поле во всех направляющих системах может иметь продольные составляющие поля 1. Поперечные волны (волны типа Т) - это волны, для которых 2. Волны, имеющие 3. Волны типа Е или ТН - для них 4. Волны НЕ типа - для них
Критическая частота и длина волн в линии передачи
При решении волнового уравнения полагают, что структура электромагнитного поля в регулярных линиях передачи зависит только от поперечных координат
где Анализируя значение постоянной распространения 1) если 2) если 3) если Из понятия критической частоты следует ряд очевидных равенств:
где Значение постоянной распространения в волноводе
где Длина волны в направляющей системе с учетом (3):
Лекция 7 Лекция 8 Волноводы круглого сечения
Геометрия поперечного сечения круглого волновода показана на рис. 12. Решение волнового уравнения для этих волноводов проводят в цилиндрической системе координат с переменными
Здесь т характеризует число полных периодов изменения поля по координате
На основании этого уравнения из решения (65) получим уравнение для определения поперечного волнового числа Таким образом, поперечное волновое число находится как п -йкорень производной функции Бесселя первого рода m -го порядка:
Для круглого волновода основной волной является волна H11, а ее ближайший высший тип - волна Е01:
Для Е и Н типов волн в круглом волноводе индекс т может принимать значение нуль, а n - всегда больше нуля. Структура поля волны H11 показана на рис. 12.
Лекция 9 Объемные резонаторы
Объемные резонаторы относятся к одним из наиболее распространенных избирательных элементов СВЧ диапазона. В отличие от низкочастотных избирательных LC -контуров в СВЧ диапазоне такие устройства реализуются в системах с распределенными параметрами. Возможность построения таких систем вытекает из уравнений Максвелла, согласно которым изменение электрического поля 1) резонансная длина волны 2) активная проводимость 3) собственная или ненагруженная добротность Параметры Резонансная длина волны. Рассмотрим условие существования электромагнитного поля в отрезке регулярной направляющей системы длиной
Отсюда из (66) на основании граничных условий (25) при определена следующим образом:
Очевидно, на основании (I) для волн типов Т и Н, укоторых полное электрическое поле Тип волны в резонаторе обозначается тремя индексами: т, n, p. Первые два определяют структуру поля в поперечном сечении, третий - характеризует поле стоячей волны в продольном сечении резонатора, например: Активная проводимость резонатора. Эта характеристика является мерой активных потерь в резонаторе и ее определяют как
где Рп - мощность активных потерь в резонаторе; Um- напряжение на входных клеммах резонатора. Так как для полых резонаторов нет однозначного определения величины напряжения Um, то понятие G является неопределенным. Обычно Um определяют как
Из выражения (67) следует, что мощность активных потерь и, следовательно, активная проводимость резонатора зависит от качества материала, его обработки и от структуры поля. Добротность резонатора. Для определения добротности резонаторов используют известное энергетическое соотношение для средних за период величин:
где Тк - период колебания;
В момент фазы колебания, когда
Значение собственной добротности с учетом (67) и (68) будет
где в выражениях (67) и (68) учтено, что для немагнитных материалов При заполнении объемного резонатора диэлектриком с потерями
а запасенная энергия На практике часто используют выражение добротности резонатора через значение активной и реактивной проводимости G, В на его входных клеммах. Для этого по аналогии с контурами запасенную энергию, мощность потерь в резонаторе и его добротность представляют как
Значение емкости С для систем с распределенными параметрами однозначно не определяется, поэтому ее выражают через входную реактивную проводимость b. Полная входная реактивная проводимость для контуров вблизи резонанса имеет вид:
где учтено, что
Соотношение (71) характеризует добротность резонатора вблизи резонансной частоты. Нагруженная и внешняя добротность резонатора. Если резонатор подключен к полезной нагрузке, то полная энергия потерь будет
где
Соответственно величина добротности через эквивалентные проводимости по аналогии с (71) примет вид:
Нагруженная добротность зависит от величины связи резонатора с нагрузкой и от его собственной добротности.
Лекция 10 Элементы теории цепей
Любой СВЧ тракт радиотехнической системы выключает в себя самые разнообразные неоднородности и элементы, которые, в конечном счете, и определяют его характеристики. Строго говоря, когда размеры этих элементов соизмеримы с длиной волны, то их расчет нужно вести методами электродинамики. Однако это сложный и неоптимальный путь. Для упрощения решения подобных задач сложную волноводную систему приводят к некоторой эквивалентной схеме, состоящей из отрезков регулярных линий и сопротивлений, а СВЧ узел рассматривают как некоторый многополюсник. Такое представление СВЧ узлов приводит к простым соотношениям между входными и выходными параметрами, и к их анализу применим математический аппарат матричной алгебры, хорошо разработанный в теории цепей. В отличие от низкочастотных цепей на СВЧ для этого метода анализа появляется ряд особенностей: 1. Нужно учитывать волновой характер процессов, что требует фиксации клеммных плоскостей, определяющих фазу процесса и длину соединяющих отрезков линий. 2. Имеется возможность распространения многих типов волн: Т, Е, Н. Если устройство допускает существование нескольких типов волн, то на выходах многополюсника каждому типу волны должна соответствовать своя пара клемм. 3. На клеммах многополюсников, соединяемых между собой, должны быть одинаковые типы волн, а преобразование типа волны должно происходить внутри многополюсника. Каждый узел представляется как некоторый многополюсник с n выходами и 2п клеммами. Если многополюсник представляет линейную цепь, то он описывается линейными алгебраическими уравнениями. На практике получили распространение два вида уравнений. В первом из них описывается связь между напряжением U и током I на клеммах посредством импедансных матриц: матрицы сопротивлений Двухполюсные системы СВЧ. Простейшими многополюсниками являются двухполюсные системы. Это схемы с одной парой клемм (рис. 14). Все свойства данной схемы характеризуются входным сопротивлением
Импедансные матрицы четырехполюсников. Связь между напряжениями и токами на выходах четырехполюсника может быть выражена шестью различными способами (рис.15).Наиболее употребительные из них три: это матрицы сопротивлений проводимости и передачи:
Система (74) характеризуется матрицей сопротивлений:
Физический смысл элементов матрицы Для взаимного четырехполюсника Вторая система (73) характеризуется матрицей проводимости Третья система (74) характеризуется матрицей передачи
Для произвольного многополюсника вводят следующие обозначения (рис. 16): падающую (входящую) волну в i -м плече обозначают через
.....
или, используя матричную запись, систему (76) запишем:
где
Физический смысл элементов матрицы | ||||||||||||||||||
|
| Поделиться: |

 , которое позволяет представить вектор
, которое позволяет представить вектор 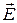 в виде градиента скалярной функции
в виде градиента скалярной функции 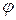 :
: , (16)
, (16) определяется как работа, совершаемая против сил поля, при перемещении положительного единичного заряда от одной точки к другой:
определяется как работа, совершаемая против сил поля, при перемещении положительного единичного заряда от одной точки к другой:

 или
или  , где в декартовой системе координат
, где в декартовой системе координат . Если в рассматриваемой области заряды отсутствуют,
. Если в рассматриваемой области заряды отсутствуют,
 имеет вид
имеет вид  . Для точечного заряда значение потенциала
. Для точечного заряда значение потенциала 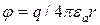
 . Эти поверхности, как следует из выражения (16), ортогональны силовым линиям электрического поля.
. Эти поверхности, как следует из выражения (16), ортогональны силовым линиям электрического поля. отсутствует электростатическое поле и не может быть постоянного объемного заряда. Для этого уравнение непрерывности
отсутствует электростатическое поле и не может быть постоянного объемного заряда. Для этого уравнение непрерывности  преобразуем на основании закона Ома
преобразуем на основании закона Ома 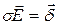 и третьего уравнения Максвелла
и третьего уравнения Максвелла  в однородное дифференциальное уравнение относительно объемной плотности заряда:
в однородное дифференциальное уравнение относительно объемной плотности заряда:
 Решение этого уравнения
Решение этого уравнения  показывает (рис. 2), что объемная плотность заряда
показывает (рис. 2), что объемная плотность заряда  . Величина
. Величина  называется временем релаксации, оно равно времени, за которое плотность заряда убывает в
называется временем релаксации, оно равно времени, за которое плотность заряда убывает в  раз.
раз. и, следовательно, в таких средах не может существовать электростатического поля
и, следовательно, в таких средах не может существовать электростатического поля 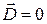 . Поэтому на основания (16) можно утверждать, что если в проводящих средах
. Поэтому на основания (16) можно утверждать, что если в проводящих средах  ,то для них
,то для них 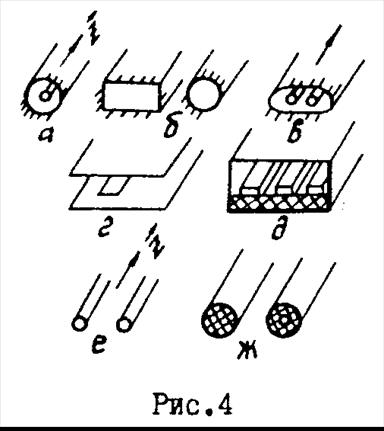 1. Линии передачи закрытого типа - это линии по своей конструкции полностью экранированные от внешнего пространства. К ним относятся коаксиальные кабели, полые волноводы экранированные двухпроводные линии (рис. 4, а, б, в) и др.
1. Линии передачи закрытого типа - это линии по своей конструкции полностью экранированные от внешнего пространства. К ним относятся коаксиальные кабели, полые волноводы экранированные двухпроводные линии (рис. 4, а, б, в) и др. и
и  . в зависимости от наличия этих составляющих проводят следующую классификацию типов волн в линиях передачи.
. в зависимости от наличия этих составляющих проводят следующую классификацию типов волн в линиях передачи.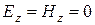 .
. и
и  ,а
,а 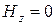 ,
, , а зависимость от продольной координаты (Z) определяется только волновым процессом, т.е.
, а зависимость от продольной координаты (Z) определяется только волновым процессом, т.е.  , где
, где  - постоянная распространения. При этом однородное волновое уравнение для регулярной линии передачи по аналогии с (29) будет
- постоянная распространения. При этом однородное волновое уравнение для регулярной линии передачи по аналогии с (29) будет ; (47)
; (47) - поперечное волновое число
- поперечное волновое число  . Длина волны в линии передачи определяется постоянной распространения
. Длина волны в линии передачи определяется постоянной распространения 
 ,можно сказать, что:
,можно сказать, что: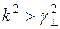 , то
, то  , то
, то  , и волновой процесс будет отсутствовать;
, и волновой процесс будет отсутствовать; , то
, то 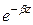 . Частота, на которой
. Частота, на которой  .
. ;
;  ;
;  , (48)
, (48)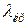 - критическая длина волны.
- критическая длина волны.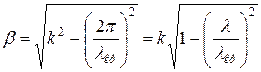 , (49)
, (49) - длина волны в свободном пространстве. Из выражения (49) следует, что волновой процесс в линии передачи будет иметь место, если
- длина волны в свободном пространстве. Из выражения (49) следует, что волновой процесс в линии передачи будет иметь место, если  .
. (50)
(50) и
и 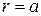 , Для электрических и магнитных волн решение этого уравнения имеет вид
, Для электрических и магнитных волн решение этого уравнения имеет вид (65)
(65) где
где 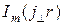 -функция Бесселя первого рода т- гопорядка аргумента
-функция Бесселя первого рода т- гопорядка аргумента  ,
,  . Значение поперечного волнового числа
. Значение поперечного волнового числа  находим из граничных условий. Для волн типа Е
находим из граничных условий. Для волн типа Е  и из (65) следует, что
и из (65) следует, что  т.е. аргумент функция Бесселя при
т.е. аргумент функция Бесселя при  и значит:
и значит: ;
; 
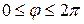 ; п - изменение поля вдоль радиуса или число полюсов функции
; п - изменение поля вдоль радиуса или число полюсов функции  определяются n -м корнем функции Бесселя m -го порядка и зависят от радиуса волновода a. Для магнитных типов волн значение поперечного волнового числа
определяются n -м корнем функции Бесселя m -го порядка и зависят от радиуса волновода a. Для магнитных типов волн значение поперечного волнового числа 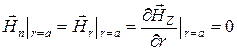
 .
. ;
; 
 ;
; 
 . Такой обмен энергиями этих полей происходит в любой точке пространства. Из уравнения энергетического баланса (26), (27) следует, что если в замкнутой области отсутствуют тепловые потери, потери на излучение, то этот обмен может происходить сколь угодно долго. Поэтому свойствами колебательной системы обладает любая изолированная система, ограниченная отражающей оболочкой. Основными параметрами резонаторов на СВЧ, в отличие от колебательных контуров с сосредоточенными параметрами, которые характеризуются L, С, R, являются:
. Такой обмен энергиями этих полей происходит в любой точке пространства. Из уравнения энергетического баланса (26), (27) следует, что если в замкнутой области отсутствуют тепловые потери, потери на излучение, то этот обмен может происходить сколь угодно долго. Поэтому свойствами колебательной системы обладает любая изолированная система, ограниченная отражающей оболочкой. Основными параметрами резонаторов на СВЧ, в отличие от колебательных контуров с сосредоточенными параметрами, которые характеризуются L, С, R, являются: , или частота fo;
, или частота fo; - мера активных потерь;
- мера активных потерь;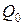 .
. ,
, 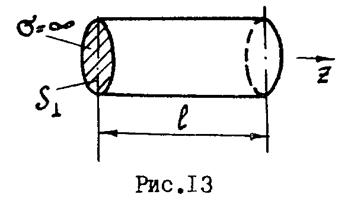 закороченной по концам при
закороченной по концам при  и
и  идеально проводящей металлической стенкой
идеально проводящей металлической стенкой  (рис. 13). Граничное условие (25) для поперечной составляющей электрического поля на стенках
(рис. 13). Граничное условие (25) для поперечной составляющей электрического поля на стенках  будет
будет  при
при  (66)
(66) , а условие при
, а условие при  , т.е.
, т.е.  . Значит, длина замкнутой направляющей системы должна быть кратной целому числу длин полуволн
. Значит, длина замкнутой направляющей системы должна быть кратной целому числу длин полуволн  где
где  . Выражение (66) показывает, что фаза поля в колебательной системе неизменна и поле носит характер стоячей волны. Резонансная частота и резонансная длина волны для резонатора длиной
. Выражение (66) показывает, что фаза поля в колебательной системе неизменна и поле носит характер стоячей волны. Резонансная частота и резонансная длина волны для резонатора длиной 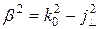 ;
; 

 ,
,  значение нуль принимать не может. Для волн типа Е равенство
значение нуль принимать не может. Для волн типа Е равенство  , а длина резонатора при
, а длина резонатора при  является неопределенной.
является неопределенной. ;
;  .
.
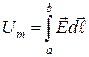 между характерными точками резонатора (а и b), например, на входных клеммах. Если допустить, что потери в резонаторе имеют место только в металлических стенках
между характерными точками резонатора (а и b), например, на входных клеммах. Если допустить, что потери в резонаторе имеют место только в металлических стенках  с поверхностным сопротивлением
с поверхностным сопротивлением  , то величину потерь в резонаторе
, то величину потерь в резонаторе  можно оценить следующим образом:
можно оценить следующим образом: (67)
(67)
 - резонансная частота;
- резонансная частота; - запасенная электромагнитная энергия.
- запасенная электромагнитная энергия.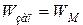 , запасенная энергия может быть подсчитана:
, запасенная энергия может быть подсчитана: (68)
(68) (69)
(69)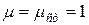 . Если пренебречь вариацией поля в резонаторе и полагать, что
. Если пренебречь вариацией поля в резонаторе и полагать, что  , то выражение (69) значительно упростится:
, то выражение (69) значительно упростится:  , где учтено, что
, где учтено, что  ,
,  , т.е. добротность резонатора пропорциональна отношению
, т.е. добротность резонатора пропорциональна отношению  .
. мощность потерь в диэлектрике определяется:
мощность потерь в диэлектрике определяется:
 . Добротность в диэлектрике будет
. Добротность в диэлектрике будет  , а при наличии магнитных потерь
, а при наличии магнитных потерь  .
. ;
; 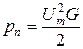 ;
;  (70)
(70)
 . Вблизи резонанса при
. Вблизи резонанса при 
 ,и выражение для реактивной проводимости b будет
,и выражение для реактивной проводимости b будет  , откуда
, откуда  . Отсюда выражение (70) для добротности может быть записано как
. Отсюда выражение (70) для добротности может быть записано как (71)
(71) , а добротность резонатора с нагрузкой характеризуется нагруженной добротностью
, а добротность резонатора с нагрузкой характеризуется нагруженной добротностью
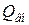 - внешняя добротность резонатора - определяется, величиной нагрузки
- внешняя добротность резонатора - определяется, величиной нагрузки


 , матрицы проводимостей
, матрицы проводимостей  и матрицы передачи
и матрицы передачи  . Во втором - используются соотношения между падающими и отраженными волнами. Их связывают волновые матрицы:
. Во втором - используются соотношения между падающими и отраженными волнами. Их связывают волновые матрицы:  - матрица рассеяния и
- матрица рассеяния и  - волновая матрица передачи.
- волновая матрица передачи. , или коэффициентом отражения Г:
, или коэффициентом отражения Г: ;
; 
 Большое значение в СВЧ устройствах имеют реактивные двухполюсники (короткозамыкатели, шлейфы, резонаторы и др.). Эти двухполюсники обладают рядом общих свойств, сформулированных в теореме Фостера. Если в двухполюснике нет активных потерь, то его сопротивление на входе чисто реактивное
Большое значение в СВЧ устройствах имеют реактивные двухполюсники (короткозамыкатели, шлейфы, резонаторы и др.). Эти двухполюсники обладают рядом общих свойств, сформулированных в теореме Фостера. Если в двухполюснике нет активных потерь, то его сопротивление на входе чисто реактивное  ;
;  ,причем
,причем  ;
;  . В отличие от низкочастотных цепей двухполюсные реактивные СВЧ устройства являются многорезонансными, так как для них резонансы имеют место на всех кратных частотах.
. В отличие от низкочастотных цепей двухполюсные реактивные СВЧ устройства являются многорезонансными, так как для них резонансы имеют место на всех кратных частотах.
 ; (72)
; (72) ; (73)
; (73) (74)
(74) ;
; ; (75)
; (75)
 . Так из (75) следует, что при
. Так из (75) следует, что при 
 - входное сопротивление при разомкнутом выходе; при
- входное сопротивление при разомкнутом выходе; при 
 -выходное сопротивление; при
-выходное сопротивление; при 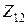
 переходные сопротивления соответственно.
переходные сопротивления соответственно. , для симметричного -
, для симметричного -  . Симметричный и взаимный четырехполюсник характеризуются двумя элементами матрицы:
. Симметричный и взаимный четырехполюсник характеризуются двумя элементами матрицы:  . Матрицу сопротивлений целесообразно использовать при последовательном соединении четырехполюсников, так как для них суммарная матрица
. Матрицу сопротивлений целесообразно использовать при последовательном соединении четырехполюсников, так как для них суммарная матрица  есть сумма отдельных
есть сумма отдельных  .
. .
. Волновые матрицы многополюсников. В уравнения (72)- (74) с импедансными матрицами входят интегральные величины: напряжения
Волновые матрицы многополюсников. В уравнения (72)- (74) с импедансными матрицами входят интегральные величины: напряжения 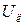 и ток
и ток  . Эти величины могут быть представлены в виде суммы падающих и отраженных волн. В СВЧ диапазоне измерение интегральных величин сложно, и обычно измеряют частоту
. Эти величины могут быть представлены в виде суммы падающих и отраженных волн. В СВЧ диапазоне измерение интегральных величин сложно, и обычно измеряют частоту  , мощность Р, КСВ или модуль и фазу коэффициента отражения. Измерение КСВ и коэффициента отражения непосредственно связано с измерением падающей и отраженной волны. Поэтому уравнения, связывающие падающие и отраженные волны многополюсника в СВЧ диапазоне, более наглядны и позволяют просто сопоставить результаты эксперимента.
, мощность Р, КСВ или модуль и фазу коэффициента отражения. Измерение КСВ и коэффициента отражения непосредственно связано с измерением падающей и отраженной волны. Поэтому уравнения, связывающие падающие и отраженные волны многополюсника в СВЧ диапазоне, более наглядны и позволяют просто сопоставить результаты эксперимента. , аотраженную или выходящую - через
, аотраженную или выходящую - через  . Пассивный линейный п -полюсник может быть описан системой п линейных алгебраических уравнений относительно волн
. Пассивный линейный п -полюсник может быть описан системой п линейных алгебраических уравнений относительно волн  ;
;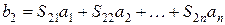 ; (76)
; (76) ;
;
 ; (77)
; (77) ,и из (5) получим
,и из (5) получим  ;
; 


