
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетические соотношения в электродинамикеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Любые физические процессы, в том числе и электромагнитные, непосредственно связаны с превращением одного вида энергии в другую в соответствии с законом сохранения энергии. В СВЧ устройствах превращения электромагнитной энергии обычно связаны о потерями на тепло, на излучение; с потерями на химические процессы, происходит также перераспределение между электрической и магнитной энергиями. Совокупность этих процессов определяет основные электрические характеристики устройства: КПД, добротность, затухание, избирательность и т.д. Математическая зависимость энергетических превращений электромагнитного поля выражается в энергетических соотношениях электродинамики. Эти соотношения для конкретной области пространства строго связаны между собой уравнением энергетического баланса. Суть этого уравнения совпадает с законом сохранения энергии для электромагнитного поля. Баланс энергии электромагнитного поля. Для изучения энергетических соотношений составляются уравнение баланса энергии для заданной области V. Это уравнение утверждает, что
т.е. мощность сторонних источников
где П - вектор Пойнтинга
Физический смыслслагаемых выражений (27) в (28) уточняется в результате их сопоставления с формулировкой баланса электромагнитной энергии (26). Так, слагаемое
где величина энергии, a
Для анализа энергетических соотношений в монохроматическом поле рассматривают уравнение баланса для средней за период мощности. Под средним за период значением функции подразумевают величину
Среднее значение изменения электромагнитной энергии за период равно нулю Таким образом, уравнение баланса для средней за период мощности:
Плоские электромагнитные волны
Как уже отмечалось выше, переменное электромагнитное поле в пространстве, свободном от источников, носит волновой характер. Оно распространяется в виде электромагнитных волн со скоростью, равной скорости света. Все свойства этого поля следуют из уравнений Максвелла, записанных для области, свободной от источников:
где волновое число Общее решение такого уравнения:
Здесь
Общее решение (29) волнового уравнения представляет собой сумму двух волновых процессов с частотой Действительное значение вектора
Охарактеризуем основные параметры прямой волны. 1. Волна, определяемая решением (4), называется плоской, так как ее параметры не зависят от поперечных координат X и У, т.е. 2. Волна является однородной, ее параметры не изменяются в пространстве; это справедливо для однородной среды без потерь. 3. Поле плоской волны не имеет продольных составляющих векторов 4. Векторы электрического и магнитного поля плоской волны в изотропной среде всегда ортогональны 5. Между амплитудами векторов магнитного и электрического полей существует строгая связь, определяемая параметрами среды
где W - волновое сопротивление среды. Для среды без потерь эта величина вещественная. Для свободного пространства 6. Изложенное в пп. 3 - 5 позволяет записать векторное отношение между электрическим и магнитным полем в следующем виде:
где 7. Фазовая скорость 8. Длина волны 1) вектор Пойнтинга
2) плотность электрической и магнитной энергии
3) скорость распространения энергии электромагнитной волны
Плоская волна в среде с потерями. В реальных средах, в которых В однородных изотропных средах с потерями поле плоской волны описывает уравнение (29), в котором волновое число K - величина комплексная. Если магнитные потери отсутствуют, то
где
Величина этого сдвига зависит от значения удельной проводимости и колеблется от
Опишем основные особенности электромагнитной волны в среде с потерями. Волна в среде с потерями является плоской неоднородной волной, так как для нее отсутствует зависимость от поперечных координат (X, У) и она убывает с расстоянием, как Охарактеризуем параметры плоской волны в реальных диэлектриках и проводниках. Для реальных диэлектриков
Из приведенных выражений следует, что свойства электромагнитной волны в диэлектрике не зависят от частоты. Для реальных проводников
Коэффициенты Понятие затухания или ослабления волны. Волна в реальной среде испытывает затухание пропорционально множителю
Для измерения ослабления вводят логарифмические величины:
т.е. 1 Неп = 8,69 дБ. Для характеристики затухания вводят понятие глубины проникновения поля в проводник
Глубина проникновения поля
Лекция 5 Поляризация электромагнитных волн Выше было показано, что вектора ноля Для описания поляризационной характеристики поля вводят понятие плоскости поляризации электромагнитной волны. За эту плоскость условно принята плоскость, проходящая через направление векторов
3. Наиболее общий случай - поле эллиптической поляризации. Поле любой поляризации может быть получено врезультате суперпозиции двух полей со взаимно ортогональной линейной поляризацией. Запишем электрическую составляющую двух линейно поляризованных волн с ортогональными векторами поляризации:
(40)
В зависимости от отношения амплитуд Для тангенса угла наклона плоскости поляризации
Таким образом, конец вектора Ев процессе распространения описывает окружность. Направление вращения определяется знаком перед углом
Условие прохождения и отражения волн на границе раздела двух сред
Электромагнитная волна, падающая на границу раздела двух сред под углом
Рассматривают два случая: 1) случай параллельной поляризации 2) случай нормальной поляризации
Падение плоской волны на границу раздела двух диэлектриков. Имеется две среды с общей плоской границей. Параметры сред равны 1) угол падения 2) отношение синуса угла падения и прохождения равно относительному показателю преломления сред Амплитудные соотношения между отраженной и прошедшей волной зависят от поляризации волны и характеризуются коэффициентом отражения Для случая параллельной поляризации
(41)
Для нормально поляризованной волны
(42)
При нормальном падении волны
Если вторая среда - идеальный проводник то на основании (41) и (42)
Падение плоской волны на границу поглощающей среды. Рассмотрим случай, когда вторая среда обладает большими потерями, т.е.
Так как величина
Приближенные граничные условия Леонтовича – Щукина Эти граничные условия рассматриваются для векторов электромагнитного поля на границе с реальным проводником
Выражение (44) называется приближенным граничным условием Леонтовича - Щукина. Эти условия применимы и для криволинейных поверхностей проводников, так как в каждой точке его поверхности
Понятие поверхностного тока и поверхностного сопротивления Поле в реальном проводнике убывает как Поверхностный эффект сильно уменьшает токонесущее сечение проводников и значительно увеличивает их сопротивление. Для оценки этого влияния вводят понятие поверхностного сопротивления
Сопоставляя (44) и (45} нетрудно заметить, что величина поверхностного сопротивления
где
Лекция 6 Линии передачи СВЧ диапазона Направляющие системы, или линии передачи, предназначены для передачи электромагнитной энергии. Существует много типов направляющих систем, каждая из которых применяется в определенной области техники СВЧ и в определенном диапазоне частот. Ниже будут рассмотрены линии передачи, которые по всем своим параметрам не имеют зависимости по продольной координате Z и имеют однородное заполнение. Такие линии называются регулярными и однородными. Их классификацию проводят следующим образом.
2. Линии полуоткрытого типа это линии, не имеющие полной экранировки от соседних линий передачи и внешнего пространства. К ним относятся различные полосковые линии передачи (рис. 4, г, д). 3. Линии открытого типа - это линии, не имеющие экранировки от внешнего пространства. К ним относятся двухпроводные линии, диэлектрические Рис. 4 волноводы и др. (рис. 4, е, ж). Основные технические требования к направляющим системам сводятся к следующему: минимальное затухание на единицу длины линии, максимальная экранировка или помехозащищенность, диапазонность, максимум допустимой мощности передачи. Конструкция линии должна обладать минимальными размерами, весом, стоимостью. Характерным для всех линий передач СВЧ диапазона является то, что в зависимости от их поперечного сечения электромагнитное поле в них может распространяться в виде бесконечно большого числа типов колебаний (типов волн), отличающихся друг от друга структурой поля. Параметры этих типов колебаний находятся из решения однородного волнового уравнения Гельмгольца с учетом граничных условий на стенках линии передачи. В общем случае в отличии от плоской волны в свободном пространстве электромагнитное поле во всех направляющих системах может иметь продольные составляющие поля 1. Поперечные волны (волны типа Т) - это волны, для которых 2. Волны, имеющие 3. Волны типа Е или ТН - для них 4. Волны НЕ типа - для них
Критическая частота и длина волн в линии передачи
При решении волнового уравнения полагают, что структура электромагнитного поля в регулярных линиях передачи зависит только от поперечных координат
где Анализируя значение постоянной распространения 1) если 2) если 3) если Из понятия критической частоты следует ряд очевидных равенств:
где Значение постоянной распространения в волноводе
где Длина волны в направляющей системе с учетом (3):
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.151 (0.01 с.) |

 ;(26)
;(26) расходуется на мощность активных потерь
расходуется на мощность активных потерь  , на изменение запасенной энергии
, на изменение запасенной энергии 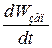 и на излученную мощность
и на излученную мощность  . С этим уравнением сопоставляется следующее математическое выражение баланса энергии, полученное путем формальных математических преобразований первых двух уравнений Максвелла со сторонними источниками:
. С этим уравнением сопоставляется следующее математическое выражение баланса энергии, полученное путем формальных математических преобразований первых двух уравнений Максвелла со сторонними источниками: (27)
(27) .Этот вектор по величине равен потоку плотности электромагнитной энергии в единицу времени и натравлен в сторону распространения энергии. Выражение (27) записано в дифференциальной форме и характеризует баланс электромагнитной энергии в каждой точке пространства. Интегральная форма записи получается при интегрировании соотношения (27) по заданному объему:
.Этот вектор по величине равен потоку плотности электромагнитной энергии в единицу времени и натравлен в сторону распространения энергии. Выражение (27) записано в дифференциальной форме и характеризует баланс электромагнитной энергии в каждой точке пространства. Интегральная форма записи получается при интегрировании соотношения (27) по заданному объему: ; (28)
; (28) соответствует мощности джоулевых потерь
соответствует мощности джоулевых потерь 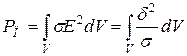 . Интеграл в левой части равенства (28) представляет собой расходуемую мощность сторонних источников
. Интеграл в левой части равенства (28) представляет собой расходуемую мощность сторонних источников  . Третье слагаемое соотношения (28) представляет поток вектора Пойнтинга через замкнутую поверхность S:
. Третье слагаемое соотношения (28) представляет поток вектора Пойнтинга через замкнутую поверхность S:  . Оно характеризует излученную мощность. Последнее слагаемое соотношения (28) представляет собой изменение запасенной магнитной и электрической энергии:
. Оно характеризует излученную мощность. Последнее слагаемое соотношения (28) представляет собой изменение запасенной магнитной и электрической энергии:
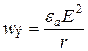 является плотностью электрической
является плотностью электрической плотностью магнитной энергии. Величина запасенной электромагнитной энергии в области V:
плотностью магнитной энергии. Величина запасенной электромагнитной энергии в области V: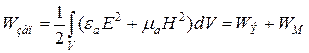
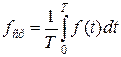 , где Т- период колебания. Слагаемые уравнения (26) дня средних за период величин имеют следующие значения:
, где Т- период колебания. Слагаемые уравнения (26) дня средних за период величин имеют следующие значения:  ;
;  ;
;  , где
, где 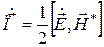 - комплексный вектор Пойнтинга. Среднее за период значение вектора Пойнтинга:
- комплексный вектор Пойнтинга. Среднее за период значение вектора Пойнтинга:  . Среднее за период значение запасенной электромагнитной энергии:
. Среднее за период значение запасенной электромагнитной энергии: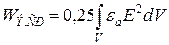 ;
; 
 , так как
, так как 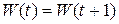 .
.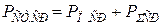 .Из этого уравнения следует, что в данном объеме в среднем за период мощность сторонних источников расходуется на джоулевы потери и на излучение электромагнитной энергии.
.Из этого уравнения следует, что в данном объеме в среднем за период мощность сторонних источников расходуется на джоулевы потери и на излучение электромагнитной энергии. ;
;  . Эти уравнения путем математических преобразований приводятся к однородному волновому уравнению Гельмгольца относительно любого из векторов электромагнитного поля. Так, для среды без потерь
. Эти уравнения путем математических преобразований приводятся к однородному волновому уравнению Гельмгольца относительно любого из векторов электромагнитного поля. Так, для среды без потерь  и для поля, зависящего только от координаты Z, т.е.
и для поля, зависящего только от координаты Z, т.е.  оно имеет вид:
оно имеет вид: , (29)
, (29) .
.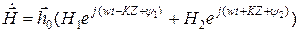 (30)
(30) ,
, 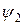 - фазы процесса;
- фазы процесса; - орт.
- орт. и амплитудами
и амплитудами  и
и  соответственно, распространяющихся навстречу друг другу. Амплитуды этих волн решением не определяются, потому что источники поля не заданы. Первое слагаемое этого решения с фазовым аргументом
соответственно, распространяющихся навстречу друг другу. Амплитуды этих волн решением не определяются, потому что источники поля не заданы. Первое слагаемое этого решения с фазовым аргументом  соответствует прямой волне, распространяющейся в направлении
соответствует прямой волне, распространяющейся в направлении  , второе слагаемое характеризует обратную волну, распространяющуюся в направлении
, второе слагаемое характеризует обратную волну, распространяющуюся в направлении  .
. прямой волны следует из решения (30):
прямой волны следует из решения (30): (31)
(31) и, следовательно, ее фазовый фронт (поверхность равных фаз) есть плоскость Z = const.
и, следовательно, ее фазовый фронт (поверхность равных фаз) есть плоскость Z = const. ,
,  . Это следует из уравнений Максвелла с учетом определения плоской волны.
. Это следует из уравнений Максвелла с учетом определения плоской волны. .
. , (32)
, (32) .
.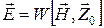 (33)
(33)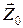 - направление распространения волны, а векторы
- направление распространения волны, а векторы 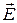 ,
,  - скорость движения фазового фронта волны на основании (31) определяется как
- скорость движения фазового фронта волны на основании (31) определяется как  .Эта скорость совпадает со значением скорости света в среде с параметрами
.Эта скорость совпадает со значением скорости света в среде с параметрами  .
.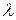 определяется как ближайшее расстояние между двумя точками поля с разностью фаз в
определяется как ближайшее расстояние между двумя точками поля с разностью фаз в  . Из решения (31) следует, что
. Из решения (31) следует, что  . Энергетические соотношения для плоской электромагнитной волны на основании (31) и (33) будут:
. Энергетические соотношения для плоской электромагнитной волны на основании (31) и (33) будут: ;
;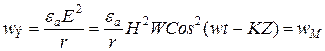 ;
;
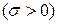 , имеют место диэлектрические или магнитные потери и плоская электромагнитная волна испытывает затухание.
, имеют место диэлектрические или магнитные потери и плоская электромагнитная волна испытывает затухание. , где
, где , (34)
, (34) , (35)
, (35) характеризует затухание волны пропорционально множителю
характеризует затухание волны пропорционально множителю 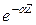 и носит название коэффициента затухания;
и носит название коэффициента затухания;  характеризует волновой процесс. Коэффициенты
характеризует волновой процесс. Коэффициенты  ; (36)
; (36) ;
;  .Между векторами электромагнитной волны в среде с потерями на основании (36) имеется фазовый сдвиг
.Между векторами электромагнитной волны в среде с потерями на основании (36) имеется фазовый сдвиг
 при
при  до
до 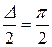 при
при  .
. , а все параметры волны
, а все параметры волны 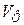 ,
, 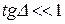 , поэтому на основании (34), (35) можно записать
, поэтому на основании (34), (35) можно записать ;
; 
 и
и  . Поэтому значения
. Поэтому значения  ; (37)
; (37) можно определить как отношение амплитуды поля в точке Z и
можно определить как отношение амплитуды поля в точке Z и 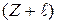 ;
;
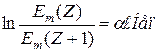 ;
;  (38)
(38)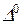 - это расстояние, на котором амплитуда волны убывает в
- это расстояние, на котором амплитуда волны убывает в  раз. Из выражений (37), (38) следует
раз. Из выражений (37), (38) следует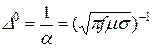 ; (39)
; (39) . Вектор
. Вектор 
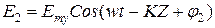
 и фаз
и фаз  и
и  суперпозиция этих полей дает любой из названных видов поляризации. Так, полю линейной поляризации соответствует в (40) разность фаз
суперпозиция этих полей дает любой из названных видов поляризации. Так, полю линейной поляризации соответствует в (40) разность фаз  где
где 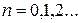 При этом тангенс угла наклона плоскости поляризации
При этом тангенс угла наклона плоскости поляризации  . Круговая поляризация получится, если
. Круговая поляризация получится, если  , а
, а  .
.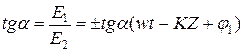 , т.е. угол наклона
, т.е. угол наклона 
 . Любое другое отношение амплитуд и фаз двух исходных полей дает поле эллиптической поляризации.
. Любое другое отношение амплитуд и фаз двух исходных полей дает поле эллиптической поляризации. , делится на волну, отраженную от границы под углом
, делится на волну, отраженную от границы под углом  , характеризующиеся коэффициентом отражения
, характеризующиеся коэффициентом отражения  , и волну, прошедшую через границу под углом
, и волну, прошедшую через границу под углом  , характеризующуюся коэффициентом передачи
, характеризующуюся коэффициентом передачи  . Лучи или направление распространения падающей, отраженной и прошедшей волны лежат в плоскости падения, ортогональной плоскости раздела сред (рис. 3). Соотношения между углами
. Лучи или направление распространения падающей, отраженной и прошедшей волны лежат в плоскости падения, ортогональной плоскости раздела сред (рис. 3). Соотношения между углами 
 , когда вектор поляризации лежит в плоскости падения волны;
, когда вектор поляризации лежит в плоскости падения волны;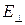 , когда вектор поляризации ортогонален плоскости падения и параллелен границе раздела двух сред.
, когда вектор поляризации ортогонален плоскости падения и параллелен границе раздела двух сред. и
и 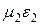 , постоянные распространения -
, постоянные распространения -  и
и  , и волновые сопротивления -
, и волновые сопротивления -  и
и  . В первой среде под углом
. В первой среде под углом 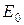 . Связь между направлениями распространения отраженной и прошедшей волн дают законы Снеллиуса:
. Связь между направлениями распространения отраженной и прошедшей волн дают законы Снеллиуса:
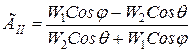
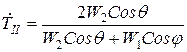



 ;
; 
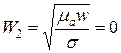
 ;
;  ;
;  , т.е. от идеальнопроводящей поверхности происходит полное отражение электромагнитной волны.
, т.е. от идеальнопроводящей поверхности происходит полное отражение электромагнитной волны. ,
,  , тогда
, тогда  .Из второго закона Снеллиуса для этого случая следует:
.Из второго закона Снеллиуса для этого случая следует: ; (43)
; (43)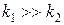 , то
, то  , и угол преломления независимо от угла падения
, и угол преломления независимо от угла падения  . Таким образом, волна, падающая на границу реального проводника, проникает в него под прямым углом;
. Таким образом, волна, падающая на границу реального проводника, проникает в него под прямым углом;  ,
, 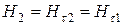 . Тогда из очевидного соотношения
. Тогда из очевидного соотношения 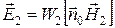 следует, что
следует, что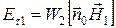 ; (44)
; (44) . Это условие должно учитываться при оценке влияния шероховатости поверхности, проводника на величину потерь.
. Это условие должно учитываться при оценке влияния шероховатости поверхности, проводника на величину потерь. , где
, где  поэтому оно проникает на небольшую глубину. Соответственно токи тоже сосредоточиваются в тонком слое на поверхности проводников и их принято называть поверхностными токами
поэтому оно проникает на небольшую глубину. Соответственно токи тоже сосредоточиваются в тонком слое на поверхности проводников и их принято называть поверхностными токами  . Это явление называют поверхностным эффектом в проводниках.
. Это явление называют поверхностным эффектом в проводниках.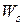 как
как ; (45)
; (45) :
: ; (46)
; (46) - глубина проникновения поля в проводник. Активная часть поверхностного сопротивления будет
- глубина проникновения поля в проводник. Активная часть поверхностного сопротивления будет 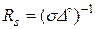 .Понятие поверхностного сопротивления значительно упрощает расчет мощности потерь в проводнике, заменяя интегрирование по объему на интегрирование по поверхности.
.Понятие поверхностного сопротивления значительно упрощает расчет мощности потерь в проводнике, заменяя интегрирование по объему на интегрирование по поверхности.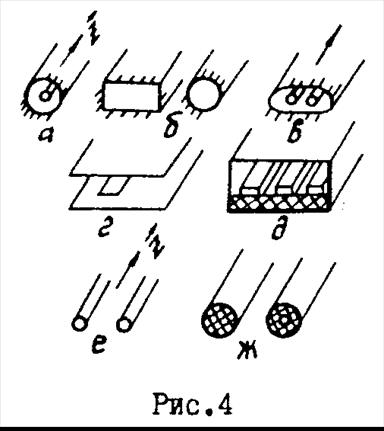 1. Линии передачи закрытого типа - это линии по своей конструкции полностью экранированные от внешнего пространства. К ним относятся коаксиальные кабели, полые волноводы экранированные двухпроводные линии (рис. 4, а, б, в) и др.
1. Линии передачи закрытого типа - это линии по своей конструкции полностью экранированные от внешнего пространства. К ним относятся коаксиальные кабели, полые волноводы экранированные двухпроводные линии (рис. 4, а, б, в) и др. и
и  . в зависимости от наличия этих составляющих проводят следующую классификацию типов волн в линиях передачи.
. в зависимости от наличия этих составляющих проводят следующую классификацию типов волн в линиях передачи.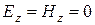 .
. и
и  ,а
,а 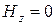 ,
, , а зависимость от продольной координаты (Z) определяется только волновым процессом, т.е.
, а зависимость от продольной координаты (Z) определяется только волновым процессом, т.е.  , где
, где  ; (47)
; (47) - поперечное волновое число
- поперечное волновое число  . Длина волны в линии передачи определяется постоянной распространения
. Длина волны в линии передачи определяется постоянной распространения 
 ,можно сказать, что:
,можно сказать, что: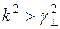 , то
, то  , то
, то  , и волновой процесс будет отсутствовать;
, и волновой процесс будет отсутствовать; , то
, то 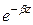 . Частота, на которой
. Частота, на которой  .
. ;
;  ;
;  , (48)
, (48)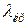 - критическая длина волны.
- критическая длина волны.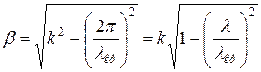 , (49)
, (49) - длина волны в свободном пространстве. Из выражения (49) следует, что волновой процесс в линии передачи будет иметь место, если
- длина волны в свободном пространстве. Из выражения (49) следует, что волновой процесс в линии передачи будет иметь место, если  .
. (50)
(50)


