
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоское деформированное состояние. Линеаризированные соотношенияСодержание книги
Поиск на нашем сайте
При плоской деформации поле напряжений и перемещений в цилиндрической системе координат таково, что:
В этом случае, функция нагружения (1.1.4.) в цилиндрической системе координат имеет вид:
Подставляя в (1.4.1) разложение (1.2.8) и приравнивая члены при одинаковых степенях
где
При
* *
Уравнениям равновесия (1.1.11) удовлетворим, полагая
где Из (1.4.2) и (1.4.6) получаем
Соотношения ассоциированного закона пластического течения для функции (1.1.5) в цилиндрической системе координат имеют вид
Откуда, линеаризируя соотношение (1.3.8), получим:
где При
Учитывая соотношения (1.1.2), (1.1.3) и (1.1.6), из (1.4.9) получаем систему уравнений для определения перемещений в пластической зоне
Введем функцию y, так что
Из соотношений (1.4.10) с учетом (1.4.11), получим уравнение для определения y
Очевидно, решение этого уравнения позволит определить перемещения в пластической зоне. Для интегрирования соотношений (1.4.12) необходимо определить величину В нулевом приближении первое соотношение (1.4.8) дает
где Интегрируя (1.4.13), получаем
Таким образом, для случая плоской деформации выведены линеаризированные соотношения EVP тела, и задача определения напряжений и перемещений для любого приближения может быть сведена к решению уравнений (1.4.7) и (1.4.12). В случае идеальной пластичности в соотношениях (1.4.1) – (1.4.12) следует положить
при
а уравнение (1.4.12) при этом записывается так
Отметим, что уравнения (1.4.7), (1.4.12), (1.4.16) принадлежат гиперболическому типу, что устанавливается обычным способом. Итак, в случае идеальной пластичности задача определения напряжений и перемещений, также как и в случае EVP сред, сводится к решению уравнений (1.4.7) с правой частью (1.4.5) и уравнения (1.4.16), соответственно. В дальнейшем с помощью соотношений (1.4.7), (1.4.12) и (1.4.16) определим напряженно-деформированное состояние в классе задач Галина-Ивлева для EVP тела и распределение напряжений и деформаций в плоских задачах теории идеальной пластичности с включениями различных очертаний. Таким образом, алгоритм построения приближенного решения задач теории течения упруговязкопластического тела с произвольным упрочнением сводится к следующему. Выполняется процедура разложения по малому параметру системы уравнений (1.1.1) – (1.1.9), описывающих рассматриваемую задачу. Рассматривается n -ое приближение, а именно: 1. Используя решение предыдущих приближений, вычисляются правые части уравнений (1.4.7), служащих для определения напряжений в пластической зоне. Так как правые части этих уравнений зависят от компонент пластической деформации искомого приближения, то в качестве первой итерации пластическим деформациям присваивается значение пластических деформаций предыдущего приближения. И, таким образом, решается уравнение (1.4.7) для определения напряжений в пластической зоне. 2. Определяются граничные условия для задачи в упругой зоне: на внешней границе, исходя из заданных при постановке задачи граничных условий (1.1.7); на границе задачи упругой и пластической областей, исходя из условий сопряжения решений на этой границе (1.1.9). Как показано в [1], граничные условия для величин любого порядка сносятся с искомой упруго-пластической границы на невозмущенную, при этом требуется знать все предыдущие приближения. 3. Находятся решения в упругой зоне согласно [1]. 4. Полученные решения для перемещений в упругой зоне используются в условиях сопряжения перемещений на упругопластической границе. 5. Решается уравнение, полученное из соотношения ассоциированного закона пластического течения (1.4.12), причем, учитывая, что правая часть этого уравнения содержит компоненту пластической деформации искомого приближения, для вычисления интеграла в правой части этого уравнения используем итерационный процесс аналогичный пункту 1. 6. Вычисляются слагаемые текущего приближения, входящие в уравнение упругопластической границы [1]. Затем процесс повторяется.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.108.8 (0.009 с.) |

 ;
; 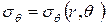 ;
;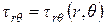 ;
;  ;
;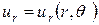 ;
;  .
.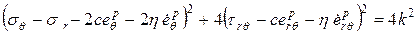 . (1.4.1)
. (1.4.1)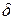 , считая при этом
, считая при этом  , получим
, получим , (1.4.2)
, (1.4.2) , (1.4.3)
, (1.4.3) . (1.4.4)
. (1.4.4)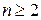 имеем
имеем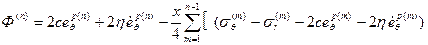 *
*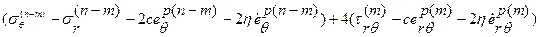 *
* (1.4.5)
(1.4.5)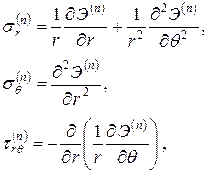 (1.4.6)
(1.4.6)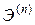 − функция напряжений Эри.
− функция напряжений Эри.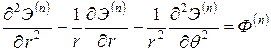 . (1.4.7)
. (1.4.7)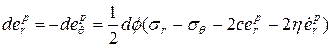 ,
,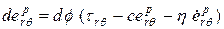 . (1.4.8)
. (1.4.8)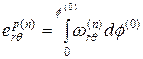 ,
, 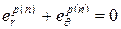 , (1.4.9)
, (1.4.9) ,
, 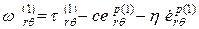 .
.
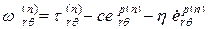
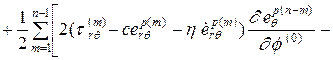
 .
.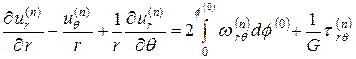 ,
,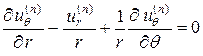 . (1.4.10)
. (1.4.10) ,
, 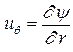 (1.4.11)
(1.4.11)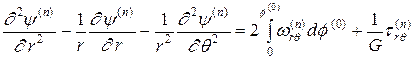 . (1.4.12)
. (1.4.12)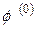 .
.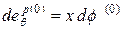 , (1.4.13)
, (1.4.13)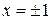 .
.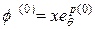 . (1.4.14)
. (1.4.14) и
и 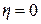 (
( ), тогда правая часть уравнения (1.4.7) примет вид
), тогда правая часть уравнения (1.4.7) примет вид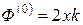 ,
,  ,
,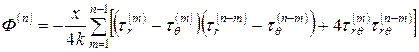 , (1.4.15)
, (1.4.15)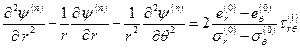 . (1.4.16)
. (1.4.16)


