
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоская задача механики деформируемого твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если решение задачи сводится к определению 2-х переменных в некоторой плоской области, то такая задача называется плоской. В МСС существуют 2 типа плоских задач: 1. плоско-деформированное состояние, 2. плоско-напряженное состояние. Рассмотрим длинное призматическое тело, упирающееся торцами в абсолютно гладкие и абсолютно жесткие плиты. К телу приложены массовые и поверхностные силы, вектор которых лежит в плоскости торца. Силы равномерно распределены вдоль оси тела. Высказанные гипотезы дают возможность предположить, что перемещения в декартовой системе координат x,y имеют следующий характер u(х,у),v(x,y), w=0. Отсюда следует, что поперечные сечения остаются плоскими и при деформировании имеет место
Плоское напряжённое состояние реализуется в тонких пластинах, ограниченных цилиндрической поверхностью. К пластине приложены усилия, вектор которых параллелен плоскости пластины и которые равномерно распределены по толщине пластины. В этом случае
В обоих случаях плоской задачи математическая постановка сводится к следующим соотношениям:
а) закон Гука в упругой области
для плоской деформации в качестве констант Е и В пластической зоне закон Гука принимается для упругих составляющих деформаций, б) в пластической зоне условие пластичности
и ассоциированного закона пластического течения для пластических компонент деформаций
в) соотношения Коши для полных деформаций
Представим решение в виде разложения по малому параметру
Очевидно, ввиду линейности уравнений (1.2.3) и (1.2.4) они сохраняют свой вид и для каждого члена разложения, поэтому для каждого члена разложения получаем решение с помощью функции напряжений Эри:
Для функции Эри в упругой области справедливо бигармоническое уравнение:
Линеаризация граничных условий и условий сопряжения Рассмотрим граничных условия в напряжениях. Для плоской задачи условия задаются на контуре
Для определенности рассмотрим полярные координаты
Подставим в (1.3.1) разложение (1.3.2) и учитывая, что компоненты
Ограничиваясь третьим приближением, из (1.3.3) получим при
Совершенно аналогично записываются линеаризированные граничные условия для Если контур границы не совпадает с окружностью
Рис. 3.1 К определению угла между нормалью к контуру и радиальным направлением.
Если уравнение границы записать в виде
где точка наверху означает дифференцирование по Уравнение границы запишем в виде:
Учитывая, что
(п)Подставив (1.3.7) и (1.3.8) в (1.3.10), получим
После представления
Следующие приближения получаются аналогично.
Условия сопряжения решений на упруго-пластичекой границе. Пусть,
Запишем уравнение контура
Применяя те же приёмы сноса условий (13) на исходную границу
Условия сопряжения для остальных компонент напряжений имеют вид, аналогичный (1.3.15). Приведём условия сопряжения для компонент перемещений.
Условия сопряжения для остальных компонент перемещений имеют вид, аналогичный (1.3.16). Граничные условия в перемещениях на части границы (назовём её
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.96 (0.008 с.) |

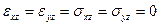 (1.2.1)
(1.2.1) . (1.2.2)
. (1.2.2)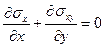 ,
, 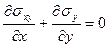 (1.2.3)
(1.2.3)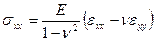 ;
;  ;
; 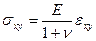 , (1.2.4)
, (1.2.4)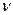 принимаются приведённые константы [3].
принимаются приведённые константы [3].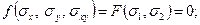 (1.2.5)
(1.2.5) (1.2.6)
(1.2.6)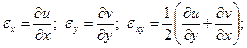 (1.2.7)
(1.2.7)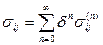 ,
, 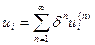 ,
,  . (1.2.8)
. (1.2.8)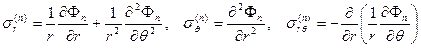 . (1.2.9)
. (1.2.9)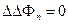 (1.2.10)
(1.2.10)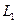 в плоскости двух переменных
в плоскости двух переменных 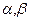 . На границе заданы нормальные усилия
. На границе заданы нормальные усилия 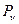 и касательные
и касательные 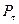
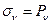 ,
,  на
на  . Уравнение границы представим в виде
. Уравнение границы представим в виде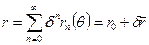 ,
,  . (1.3.2)
. (1.3.2)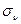 ,
, 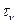 могут быть так же представлены в виде ряда получим при
могут быть так же представлены в виде ряда получим при 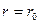
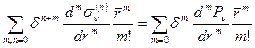 ,
,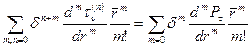 . (1.3.3)
. (1.3.3)
 (1.3.4)
(1.3.4)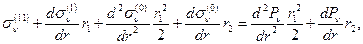 (1.3.5)
(1.3.5)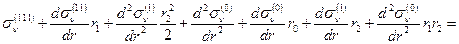
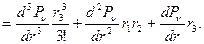 (1.3.6)
(1.3.6) , заменив в предыдущих соотношениях
, заменив в предыдущих соотношениях 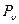 на
на 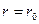 , то необходимо учесть угол нормали к контуру
, то необходимо учесть угол нормали к контуру 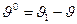 при записи нормальных и касательных напряжений на заданном контуре через компоненты напряжений в полярной системе координат
при записи нормальных и касательных напряжений на заданном контуре через компоненты напряжений в полярной системе координат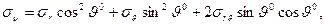
 (1.3.7)
(1.3.7)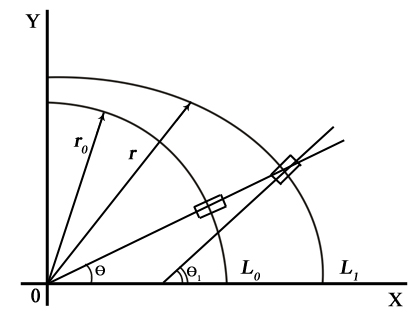
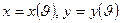 , то
, то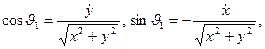 (1.3.8)
(1.3.8) .
.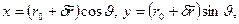

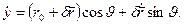 (1.3.9)
(1.3.9)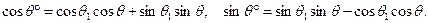 (,) (1.3.10)
(,) (1.3.10)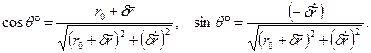 (1.3.11)
(1.3.11)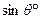 и
и 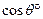 рядом по
рядом по 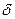 , получим
, получим
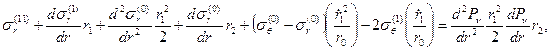
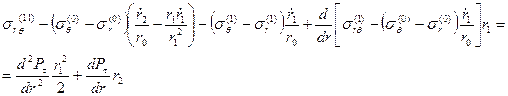 (1.3.12)
(1.3.12)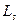 - граница между упругой и пластической областями. Решения в упругой и пластической областях должны удовлетворять условиям непрерывности на границе
- граница между упругой и пластической областями. Решения в упругой и пластической областях должны удовлетворять условиям непрерывности на границе  (1.3.13)
(1.3.13)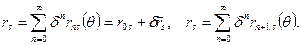 (1.3.14)
(1.3.14) что и в граничных условиях, получим:
что и в граничных условиях, получим: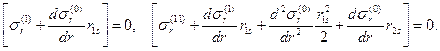 (1.3.15)
(1.3.15)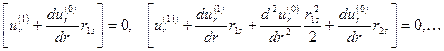 (1.3.16)
(1.3.16) ) выписываются по тому же алгоритму, что и для напряжений на границе
) выписываются по тому же алгоритму, что и для напряжений на границе 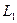 : сначала уравнение границы представим в виде (1.3.14), подставляя это разложение в (1.3.16), получим разложения аналогичные (1.3.12) для
: сначала уравнение границы представим в виде (1.3.14), подставляя это разложение в (1.3.16), получим разложения аналогичные (1.3.12) для 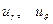 при
при 


