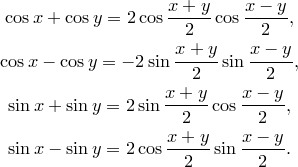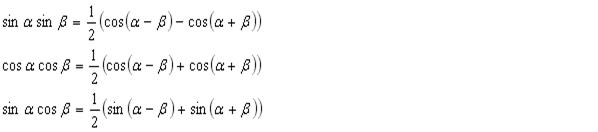Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
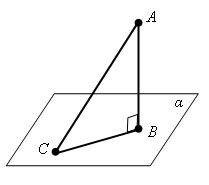
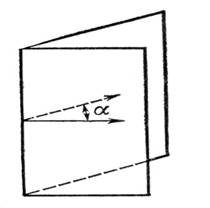
Прямые перпендикулярные к плоскостиСодержание книги Поиск на нашем сайте Прямая перпендик к плоскости если она перпендик к любой прямой лежащей в этой плоскости Теорема: если одна из двух || прямых перпендик к плоскости то и другая прямая перпендик к этой плоскости Док-во: Теорема: если 2 прямые перпендик то они || Признак перпендикулярности прямой и плоскости Там большое докозательство я пишу на телефоне так что позже капельку напишу. Теорема о прямой перпендикулярной к плоскости Теорема: 26.Перпендикуляр и наклонная. Пусть даны плоскость и не лежащая на ней точка. Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость. Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной. AB – перпендикуляр к плоскости α. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и её проекцией на плоскость. Если прямая перпендикулярна к плоскости, то её проекцией на эту плоскость является точка персечения этой прямой с плоскостью. В таком случае угол между прямой и плоскостью считается раным 90. Если прямая параллельна плоскости, то её проекцией на плоскость является прямая,параллельная данной.В этом случае понятие угла между прямой и плоскостью мы не вводим. (Иногда договариваются считать, что угол между параллельными прямой и плоскостью равен 0). 27.Двугранный угол Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей граицей а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а- общая граница полуплоскостей- называется ребром двугранного угла. Двугранные углы измеряются линейным углом. Линейный угол -это угол образованный пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
Двугранный угол называется прямым(острым, тупым), если он равен 90(меньше 90,больше 90). 28. Синус и косинус суммы и разности аргументов. sin(x+y)=sinxcosy+cosxsiny, cos(x+y)=cosxcosy-sinxcosy. Эти формулы обычно называют синус суммы и косинус суммы. Рассмотрим выражение sin(x-y). Если переписать его в виде sin(x+(-y)), то появляется возможность применить формулу суммы для аргументов x и –y: sin(x+(-y))=sinxcos(-y)+cosxsin(-y). (1) А теперь воспользуемся тем,что cos(-y)=cosy, sin(-y)=-siny. Это позволит правую часть равенства (1) переписать в виде sinxcosy-cosxsiny. Таким образом, получилась формула синуса разности: sin(x-y)=sinxcosy-cosxsiny. Аналогичные рассуждения позволяют вывести формулу косинуса разности: cos(x-y)=cos(x+(-y))=cosxcos(-y)-sinxsin(-y)=cosxcosy+sinxsiny. Итак, cos(x-y)= cosxcosy+sinxsiny. 29.Тангенс суммы и разности аргументов. tg(x+y)=tgx+tgy/1-tgxtgy tg(x-y)=tgx-tgy/1+tgxtgy. При этом предполагается, что все тангенсы имеют смысл, т.е. что x≠π/2+πn, y≠π/2+πk, x+y≠π/2+πm(для первой формулы), x-y≠π/2+πm(для второй формулы). P.S Там ещё в конце этого параграфа есть док-во, но там пипеец..
30. Формулы двойного аргумента Тригонометрические формулы, позволяющие выразить sin 2x, cos 2x, tg 2x через sin x, cos x, tg x формулами двойного аргумента. 1.Рассмотрим выражение sin 2x, представив при этом 2х в виде х+х (применяя к выражению формулу синуса суммы): Sin 2x =sin(x+x)=sinx*cosx+cosx*sinx= 2sinx*cosx Таким образом, Sin 2x=2sinx*cosx 2.Рассмотрим выражение cos 2x, представив при этом 2х в виде х+х (применяя формулу косинуса суммы): Cos 2x =cos(x+x)=cosx*cosx-sinx*sinx= cos2x-sin2x Таким образом, Cos 2x =cos2x-sin2x 3. аналогично рассмотрим tg 2x: tg х + tg х 2 tg х tg 2x = tg (x + х) = —————— = ————— 1 – tg х tg х 1 – tg2 х Таким образом, Tg х tg 2x = ————— Tg2 х Другие формулы двойного аргумента:
31.Преобразование сумм тригонометрических функций в произведение Теорема. Для любых Доказательство. Все четыре формулы доказываются преобразованием правой части в сумму
32 .Преобразование произведения тригонометрических функций в суммы
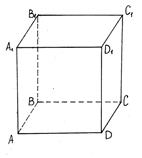
33. Параллелепипед Параллелепипед - призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.
Типы параллелепипеда Различается несколько типов параллелепипедов: · Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники; · Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — параллелограммы; · Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям. Основные элементы Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями. Свойства · Параллелепипед симметричен относительно середины его диагонали. · Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. · Противолежащие грани параллелепипеда параллельны и равны. · Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений Основные формулы Прямой параллелепипед · Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота · Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания · Объём V=Sо*h
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

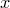 и
и  справедливы равенства
справедливы равенства