
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение производной для нахождения наибольших и наименьших значений величинСодержание книги
Поиск на нашем сайте
1. Найти область определения функции, 2. Исследовать функцию на четность. 3. Исследовать функцию на периодичность. 4. Найти точки пересечения графика с осями координат. 5. Определить промежутки знакопостоянства. 6. Исследовать функцию на границах области. Найти асимптоты. 7. Исследовать функцию на экстремум. 8. Составить таблицу значений функции для некоторых значений аргумента. 9. Используя все полученные результаты,построить график функции.
Перпендикулярность плоскостей. Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
Теорема.
Доказательство: Пусть которой пересекаются плоскости Докажем, что плоскости Проведем через прямые а и b плоскость Теорема доказана.
Теорема о трех перпендикулярах. Теорема. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна к наклонной.
Доказательство:
Пусть
Обратная теореме о трех перпендикулярах.
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции. Доказательство:
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на эту прямую. Скрещивающиеся прямые.
Невозможно. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, и он перпендикулярен каждой из этих прямых. Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, каждая из которых проходит через одну прямую параллельно другой.
Имеем две скрещивающиеся прямые a и b. Через каждую из них проведена плоскость(плоскость
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.137 (0.007 с.) |

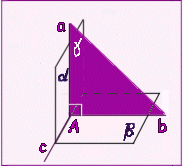 Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.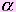 - плоскость, b - перпендикулярная ей прямая,
- плоскость, b - перпендикулярная ей прямая, 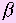 - плоскость проходящая через прямую b, и с - прямая по
- плоскость проходящая через прямую b, и с - прямая по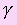 . Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскости
. Она перпендикулярна прямой с, так как прямые а и b перпендикулярны, то плоскости 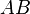 — перпендикуляр к плоскости
— перпендикуляр к плоскости 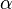 ,
, 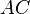 — наклонная и
— наклонная и  — прямая в плоскости
— прямая в плоскости 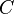 и перпендикулярная проекции
и перпендикулярная проекции 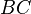 . Проведем прямую
. Проведем прямую  параллельно прямой
параллельно прямой 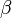 (параллельные прямые определяют плоскость, причем только одну). Прямая
(параллельные прямые определяют плоскость, причем только одну). Прямая  Пусть АВ — перпендикуляр к плоскости α, АС — наклонная и с — прямая в плоскости α, проходящая через основание наклонной С. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости α (по этой теореме, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой с. Проведем через параллельные прямые АВ и СК плоскость β (параллельные прямые определяют плоскость, причем только одну). Прямая с перпендикулярна двум прямым лежащим в плоскости β, это АС по условию и СК по теореме о трех перпендикулярах, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС. Другими словами проекция ВС перпендикулярна прямой с, лежащей в плоскости α.
Пусть АВ — перпендикуляр к плоскости α, АС — наклонная и с — прямая в плоскости α, проходящая через основание наклонной С. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости α (по этой теореме, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой с. Проведем через параллельные прямые АВ и СК плоскость β (параллельные прямые определяют плоскость, причем только одну). Прямая с перпендикулярна двум прямым лежащим в плоскости β, это АС по условию и СК по теореме о трех перпендикулярах, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС. Другими словами проекция ВС перпендикулярна прямой с, лежащей в плоскости α.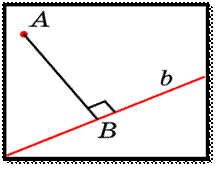 44. Расстояние от точки до прямой. Расстояние между скрещивающимися прямыми.
44. Расстояние от точки до прямой. Расстояние между скрещивающимися прямыми.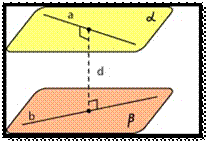 Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость
Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость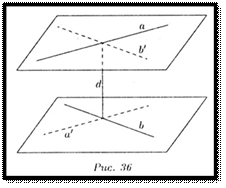 Пример:
Пример: проходит через а, плоскость проходит через b), параллельная другой прямой. Отрезки параллельных прямых, заключенные между параллельных прямых, равны.
проходит через а, плоскость проходит через b), параллельная другой прямой. Отрезки параллельных прямых, заключенные между параллельных прямых, равны.


