
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи. Метод возмущенийСодержание книги
Поиск на нашем сайте
Введение Одной из наиболее сложных задач в разделе математической теории пластичности является неодномерная упруговязкопластическая задача. Сложность ее состоит в том, что граница между областью, которая перешла в пластическое состояние, и областью, деформирующейся упруго, заранее неизвестна, и ее нужно определять в ходе решения задачи, уравнения же в упругой и пластической областях принадлежат к разным типам. Пластические свойства материалов проявляются весьма разнообразно в зависимости от условий работы, типа нагрузок, структуры материала и т.д.
ПОСТАНОВКА ЗАДАЧИ. МЕТОД ВОЗМУЩЕНИЙ
Определяющие соотношения, граничные условия, условия сопряжения теории EVP тела Рассмотрим упруговязкопластическое тело [2], механическая модель которого показана на рис. 1.1.
Рис 1.1 Модель упругопластического тела. Индексы e, e1, p и v обозначают соответственно упругий, пластический и вязкий механизмы. Данная модель ведет себя как анизотропно упрочняющаяся упругопластическая среда. В отличие от известных (тело Бингама, вязкопластическая среда Ильюшина и др.) наиболее полно учитывает свойства реальных тел. Действительно, с неограниченным ростом жесткости внутреннего упругого элемента и сколь угодно малом коэффициенте сцепления механизма сухого трения связь между элементами e1 и v становится жесткой и имеет место модель вязкопластического тела Бингама. Приведем основные соотношения, которые используются при описании напряженно-деформированного состояния упруговязкопластического тела в рамках теории течения [2]. 1. Уравнения равновесия в напряжениях
где
2. Соотношения, связывающие полные, упругие и пластические деформации
где
3. Соотношения закона Гука, связывающие напряжения и упругие деформации,
где
4. Уравнение поверхности нагружения
где
Очевидно, если 5. Соотношения ассоциированного закона пластического течения
где 6. Соотношения Коши, связывающие компоненты тензора деформаций
7. Граничные условия в напряжениях
на части поверхности, где заданы усилия
на части поверхности, где известны перемещения 8. Условия непрерывности вектора напряжений и перемещений на упругопластической границе
Здесь и далее квадратные скобки обозначают разность значений выражений, заключенных в скобки, соответствующих упругой и пластической областям. По индексам, повторяющимся два раза, предполагается суммирование от 1 до 3, если не оговорено противное. Нижний индекс, стоящий после запятой, указывает на дифференцирование по координате, соответствующей этому индексу. Уравнения (1.1.1)-(1.1.9) при учете условия несжимаемости
представляют систему уравнений, описывающих напряженно-деформированное состояние упрочняющегося упруговязкопластического тела. Так как в дальнейшем будем исследовать классы задач в основном в цилиндрической и сферической системах координат, то приведем вид уравнений равновесия (1.1.1) и формул Коши (1.1.6) в этих системах координат.
Уравнения равновесия имеют вид: · в цилиндрической системе координат (
· в сферической системе координат (
Формулы Коши: · в цилиндрической системе координат
· в сферической системе координат
Введение Одной из наиболее сложных задач в разделе математической теории пластичности является неодномерная упруговязкопластическая задача. Сложность ее состоит в том, что граница между областью, которая перешла в пластическое состояние, и областью, деформирующейся упруго, заранее неизвестна, и ее нужно определять в ходе решения задачи, уравнения же в упругой и пластической областях принадлежат к разным типам. Пластические свойства материалов проявляются весьма разнообразно в зависимости от условий работы, типа нагрузок, структуры материала и т.д.
ПОСТАНОВКА ЗАДАЧИ. МЕТОД ВОЗМУЩЕНИЙ
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.119 (0.005 с.) |


 , (1.1.1)
, (1.1.1) − компоненты тензора напряжений,
− компоненты тензора напряжений, − ковариантная производная по
− ковариантная производная по  – ой координате.
– ой координате. , (1.1.2)
, (1.1.2) − компоненты тензора деформаций,
− компоненты тензора деформаций,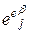 − компоненты тензора упругих деформаций,
− компоненты тензора упругих деформаций, − компоненты тензора пластических деформаций.
− компоненты тензора пластических деформаций. , (1.1.3)
, (1.1.3) − компоненты девиатора тензора напряжений,
− компоненты девиатора тензора напряжений, − модуль сдвига.
− модуль сдвига. , (1.1.4)
, (1.1.4) ,
, − коэффициент упрочнения,
− коэффициент упрочнения, − коэффициент вязкости,
− коэффициент вязкости, − компоненты тензора скоростей пластических деформаций,
− компоненты тензора скоростей пластических деформаций, − предел текучести,
− предел текучести, − время.
− время. и
и  , то поверхность нагружения изотропно расширяясь, одновременно перемещается в пространстве напряжений, так как имеет место пластическое деформирование материала с изотропным и кинематическим упрочнением.
, то поверхность нагружения изотропно расширяясь, одновременно перемещается в пространстве напряжений, так как имеет место пластическое деформирование материала с изотропным и кинематическим упрочнением.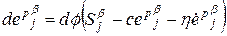 , (1.1.5)
, (1.1.5) − скалярный положительный множитель.
− скалярный положительный множитель. и вектора перемещений
и вектора перемещений 
 . (1.1.6)
. (1.1.6) , (1.1.7)
, (1.1.7) (
( − компоненты вектора нормали), и граничные условия для перемещений
− компоненты вектора нормали), и граничные условия для перемещений , (1.1.8)
, (1.1.8) .
. . (1.1.9)
. (1.1.9)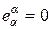 (1.1.10)
(1.1.10) )
) ,
, , (1.1.11)
, (1.1.11) ;
; )
) ,
, , (1.1.12)
, (1.1.12) .
. ,
, ,
,  , (1.1.13)
, (1.1.13) ;
; ,
, , (1.1.14)
, (1.1.14) .
.


