Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное расположение плоскостейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Плоскости по отношению друг к другу могут занимать два положения: быть параллельными или пересекаться. Параллельные плоскости не имеют ни одной общей точки. Если плоскости параллельны, то на КЧ параллельны их одноименные следы. На рисунке 3.11 изображены две параллельные плоскости:
Рис. 3.11 Признак параллельности плоскостей: Плоскости параллельны, если пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости.
Рис. 3.12 Если две плоскости не параллельны, то они обязательно пересекаются и результатом их пересечения является прямая. Рассмотрим сначала частные случаи пересечение двух плоскостей. Пример 1. Пересекаются плоскость общего положения Этот случай является основой для решения задач на пересечение плоскостей в общем виде. Так как одна из заданных плоскостей проецирующая, то все геометрические элементы, включая и линию пересечения плоскостей l, спроецируются на след этой плоскости. На КЧ горизонтальная проекция линии пересечения определяется исходя из принадлежности ее проецирующей плоскости
Рис. 3.13 Пример 2. Пересекаются плоскости общего положения, заданные следами.
Рис. 3.14 В этом случае следы плоскости пересекаются в пределах чертежа, следовательно, линия пересечения этих плоскостей строится по двум точкам, являющимся следами линии пересечения, которые находятся в точках пересечения одноименных следов плоскостей. Для построения линии пересечения плоскостей в общем случае необходимо найти две точки, одновременно принадлежащие этим плоскостям, или одну общую точку, если известно направление линии пересечения. Направление линии пересечения известно в том случае, если: 1) пересекающиеся плоскости содержат взаимно-параллельные прямые (линия пересечения плоскостей параллельна этим прямым); 2) две пересекающиеся плоскости перпендикулярны третьей плоскости (линия пересечения перпендикулярна этой плоскости).
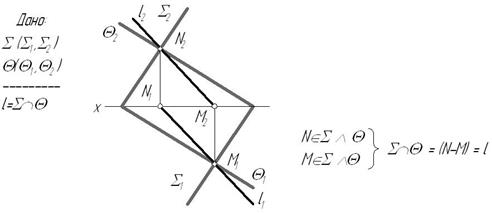
Общая точка для двух пересекающихся плоскостей в общем случае определяется с помощью вспомогательной плоскости частного положения, также пересекающей заданные плоскости по прямой (рис. 3.15).
Рис. 3.15 Общий случай: Пересекаются плоскости общего положения.
Рис. 3.16
Лекция 4 Взаимное расположение прямой и плоскости Для прямой и плоскости возможны три случая их взаимного расположения: 1) прямая линия может принадлежать плоскости[5]; 2) быть параллельна плоскости; 3) пересекаться с ней. Параллельность прямой и плоскости Признак параллельности прямой и плоскости хорошо известен из курса стереометрии: Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.
Рис. 3.16 Определение видимости на КЧ Для улучшения наглядности изображений, заданных на КЧ, принято видимые для наблюдателя линии показывать сплошными, а невидимые – штриховыми линиями. При этом предполагается, что: 1) плоскости и поверхности непрозрачны; 2) луч зрения от наблюдателя всегда попадает перпендикулярно к той плоскости проекций, относительно которой определяется видимость. На рисунке 3.17 заданы две пары точек: 1) точки А и В, находящиеся на одном проецирующем луче, направленном перпендикулярно горизонтальной плоскости проекций 2) точки С и D, через которые проходит проецирующий луч, перпендикулярный фронтальной плоскости проекций
Рис. 3.17 Необходимо определить видимость точек относительно горизонтальной и фронтальной плоскостей проекций. Если на КЧ какие-либо две проекции точек совпадают, то для наблюдателя будет видима та точка, проекция которой находится дальше от оси проекций. Точки А и В, С и D называются точками, конкурирующими в видимости, а сам метод определения видимости – методом конкурирующих точек. Конкурирующими в видимости точками называются точки, лежащие на одном проецирующем луче, но принадлежащие разным геометрическим объектам.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.188.152 (0.008 с.) |

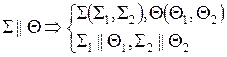 .
.
 .
.
 и горизонтально-проецирующая плоскость
и горизонтально-проецирующая плоскость 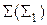 , заданная следом.
, заданная следом. ,а фронтальная проекция – по принадлежности второй заданной плоскости.
,а фронтальная проекция – по принадлежности второй заданной плоскости.


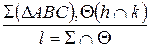 .
.


 .
.
 ;
; .
.