
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Натуральная величина отрезка прямой общего положения. Метод прямоугольного треугольникаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований. Существует несколько методов нахождения натуральной величины отрезка прямой общего положения и углов наклона его к плоскостям проекций. Одним из этих методов является метод прямоугольного треугольника, в котором находится зависимость длины проекции отрезка от его истинной величины.
Рис. 2.18
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций Для определения натуральной величины отрезка прямой общего положения и углов наклона ее к плоскости проекций на КЧ необходимо построить прямоугольный треугольник: 1. Первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов). 2. Из проекции любого конца отрезка ( 3. Гипотенуза полученного таким образом прямоугольного треугольника равна длине заданного отрезка. 4. Угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.
Рис. 2.19 Следовательно, для определения угла наклона отрезка к горизонтальной плоскости проекций прямоугольный треугольник строится на базе горизонтальной проекции отрезка, к фронтальной плоскости проекций – на базе фронтальной проекции, к профильной плоскости проекций – на базе профильной проекции. 2.3. Плоскость. Способы ее задания, положение относительно плоскостей проекций Положение плоскости в пространстве может быть однозначно определено: 1) тремя точками, не лежащими на одной прямой (рис. 2.20 а); 2) прямой и точкой, не лежащей на этой прямой (рис. 2.20 б); 3) двумя параллельными прямыми (рис. 2.20 в); 4) двумя пересекающимися прямыми (рис. 2.20 г); 5) плоской фигурой (рис. 2.20 д); 6) следом плоскости (рис. 2.20 е). На КЧ плоскость задается проекциями этих элементов, но не ограничивается ими, т.к. она безгранична и бесконечна. Всегда от одного способа задания плоскостей можно перейти к другому. Например, соединив между собой точки А, В и С отрезками прямых линий, можно получить плоскость, заданную треугольником
Рис. 2.20 След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций. Соответственно различают горизонтальный, фронтальный и профильный следы плоскости. Задание плоскости следами дает наиболее наглядное представление о положении плоскости в пространстве. В системе двух плоскостей проекций плоскость в общем случае имеет два следа (рис. 2.21 а, б). Точки пересечения двух следов на оси проекций называются точками схода следов. Для упрощения решения задач на практике обычно переходят от такого способа задания плоскости к заданию ее двумя пересекающимися прямыми нулевого уровня[2]: горизонталью, лежащей в горизонтальной плоскости проекций и совпадающей с горизонтальным следом плоскости
Рис. 2.21 Классификация плоскостей относительно плоскостей проекций аналогична классификации прямых: плоскости относительно плоскостей проекций могут занимать общее или частное положение. Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций. Плоскость общего положения пересекает все плоскости проекций (рис. 2.21).[3] Признаки и свойства плоскости общего положения: 1) Следы плоскости общего положения не параллельны и не перпендикулярны ни одной из осей проекций. 2) Любой плоский геометрический объект (отрезок или фигура), лежащий в плоскости, проецируется на любую из плоскостей проекций с искажением. Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им. Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью. Существует три вида проецирующих плоскостей: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след проекций) на ту плоскость проекций, к которой они перпендикулярны. 1. Горизонтально-проецирующая плоскость – плоскость перпендикулярная горизонтальной плоскости проекций. Признаки и свойства горизонтально-проецирующей плоскости: 1) горизонтальный след плоскости 2) горизонтальные проекции всех точек, прямых и плоских фигур, лежащих в горизонтально-проецирующей плоскости, находятся на ее горизонтальном следе
Рис. 2.22 2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.
Рис. 2.23 Признаки и свойства фронтально-проецирующей плоскости: 1) фронтальный след плоскости 2) фронтальные проекции всех точек, прямых и плоских фигур, лежащих во фронтально-проецирующей плоскости, находятся на ее фронтальном следе 3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Рис. 2.24 Признаки и свойства профильно-проецирующей плоскости: 1) горизонтальный и фронтальный следы плоскости 2) профильные проекции всех точек, прямых и плоских фигур, лежащих в профильно-проецирующей плоскости, находятся на ее профильном следе. Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня. Все точки этой плоскости одинаково удалены от той плоскости проекций, к которой она параллельна. Любой отрезок или плоская фигура, лежащие в плоскости уровня, проецируются без искажения на параллельную ей плоскость проекций. Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня. Плоскости уровня пересекают только две плоскости проекций, поэтому, в отличие от ранее рассмотренных плоскостей, имеют только два следа. 1. Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций. Признаки и свойства горизонтальной плоскости: 1) фронтальный и профильный следы плоскости 2) фронтальные проекции всех точек, прямых и плоских фигур, лежащих в горизонтальной плоскости, находятся на ее фронтальном следе, профильные проекции – на профильном; 3) горизонтальные проекции плоских фигур, лежащих в плоскости, равны их натуральным величинам.
Рис. 2.25 2. Фронтальная плоскость – плоскость, параллельная фронтальной плоскости проекций.
Рис. 2.26 Признаки и свойства горизонтальной плоскости: 1) горизонтальный и профильный следы плоскости 2) горизонтальные проекции всех точек, прямых и плоских фигур, лежащих во фронтальной плоскости, находятся на ее горизонтальном следе, профильные проекции – на профильном; 3) фронтальные проекции плоских фигур, лежащих в плоскости, равны их натуральным величинам. 3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций. Признаки и свойства профильной плоскости: 1) фронтальный и горизонтальный следы плоскости 2) фронтальные проекции всех точек, прямых и плоских фигур, лежащих в профильной плоскости, находятся на ее фронтальном следе, горизонтальные проекции – на горизонтальном; 3) профильные проекции плоских фигур, лежащих в плоскости, равны их натуральным величинам.
Рис. 2.27 Лекция 3
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.008 с.) |



 . Через точку А проведем линию, параллельную плоскости
. Через точку А проведем линию, параллельную плоскости  , один из катетов которого (
, один из катетов которого ( ) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис. 2.18).
) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис. 2.18). или
или  ) под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций.
) под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций.
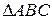 (рис. 2.20 а, д).
(рис. 2.20 а, д).
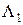 , и фронталью, располагающейся во фронтальной плоскости проекций и совпадающей с фронтальным следом плоскости
, и фронталью, располагающейся во фронтальной плоскости проекций и совпадающей с фронтальным следом плоскости  (рис.2.21 а, в).
(рис.2.21 а, в).
 располагается наклонно к осям проекций 0x и 0y и определяет углы наклона этой плоскости к фронтальной (
располагается наклонно к осям проекций 0x и 0y и определяет углы наклона этой плоскости к фронтальной ( ) и профильной (
) и профильной ( ) плоскостям проекций;
) плоскостям проекций; , его называют следом проекций.
, его называют следом проекций.

 ) и профильной (
) и профильной ( .
.
 располагаются параллельно осям проекций 0x и 0y соответственно;
располагаются параллельно осям проекций 0x и 0y соответственно;

 располагаются параллельно осям проекций 0x и 0z соответственно;
располагаются параллельно осям проекций 0x и 0z соответственно; располагаются параллельно осям проекций 0z и 0y соответственно;
располагаются параллельно осям проекций 0z и 0y соответственно;



