
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система пропорционирования равносторонних треугольниковСодержание книги
Поиск на нашем сайте
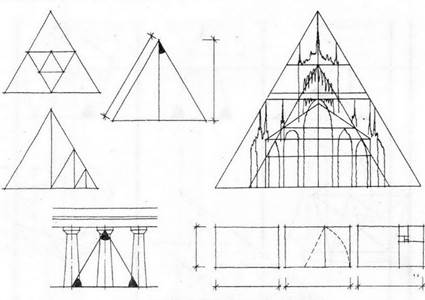
Система вписанных равносторонних треугольников дает ряд на основе двух чередующихся отношений: стороны треугольника к высоте (2/ V 3) и высоты к половине стороны (v'a). Пропорциониро-вание на основе равностороннего треугольника особенно широко применялось в средневековье» где система триангулирования пронизывала всю структуру готических соборов (рис.97), однако отношения, свойственные этой системе, могут быть обнаружены и в архитектуре других эпох, например, в архитектуре Древней Греции.
36) Наиболее известным и в то же время загадочным рядом средних чисел является так называемое отношение золотого сечения. Термин "золотое сечение" был введен Леонардо да Винчи для известного еще пифагорейцам описанного Эвкли- дом деления отрезка в так называемом "крайнем и среднем отношении", при котором большая его часть является средней пропорциональной между всем отрезком и меньшей частью.Если длину отрезка принять за единицу, то его части будут выражаться иррациональными числами X = 0,618, а — х = 0,382. На основе этих чисел может быть получен геометрический ряд... — 0,146 — 0,236 — 0,382 — 0,618 — 1 — 1,618 — 2,618 — 4,236 — 6,854 —..., обнаруживаемый при рассмотрении самого широкого круга явлений природы, искусства и архитектуры. Не случайно знаменитый итальянский философ и математик Фра Лука Паччоли называл золотое сечение "божественной пропорцией", а немецкий ученый А.Цейзинг провозгласил золотое сечение универсальной пропорцией, равно характерной для современных творений природы и искусства. Золотое сечение использовал в своем творчестве И.В.Жолтовский, а Ле Корбюзье положил его в основу своего "Моду- лора". Золотое сечение выражают обычно числом 1,618 или обратным ему числом 0,618, для которых по предложению Т.Куба и М.Бара приняты символы Ф и 1/Ф. Эти числа являются знаменателями - возрастающего (Ф) и убывающего, (l/Ф) рядов золотого сечения.ч Интересной особенностью этих чисел является их способность при сложении с единицей (для Ф) и при вычитании из единицы, (для 1/Ф) давать квадраты самих себя, т.е. 1 + Ф + Ф2; 1 — 1/Ф = (1/Ф)2. Золотое сечение — это единственная геометрическая прогрессия, обладающая признаком аддитивного ряда (Ф3 = Ф1 + Ф2).
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью
и, наоборот, отношение меньшей части к большей
Число
Настя ГР Настя ГР. Настя ГР. Посліідовність Фібоніччі Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — числова послідовність
і т.д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях - комбінаторних, числових, геометричних. В природі числа Фібоначчі часто трапляються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: 1/3 повного оберту в ліщини, 2/5 - у дуба, 3/8 - у тополі і груші, 5/13 - у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі. Числа Фібоначчі щільно пов'язані з золотим перетином
Ідея полягає в наступному. F_n = F_(n-1) + F_(n-2) F_(n+1) = F_n + F_(n-1) = 2*F_(n-1) + F_(n-2) Покладемо F0 = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,.. За свідченням Месселя, античні зодчі в якості джерела гармонії архітектурних будівель незмінно використовували геометричні проекції п'яти так званих «Платонових тіл», що відображають відповідно до їхніх представлень загальну гармонію світу. Це вписані в сферу правильні багатогранники з числом граней 4, 6, 8, 12, 20. Е. Мессель, зокрема, особливо виділяє пропорції, засновані на вписаному в коло правильному десятіугольніке. Ставлення радіусу кола до сторони багатокутника виражається ірраціональним числом (√ 5 +1) / 2 = 1,61 8 і дає пропорцію так званого «золотого перетину».
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.163.224 (0.006 с.) |

 35)
35)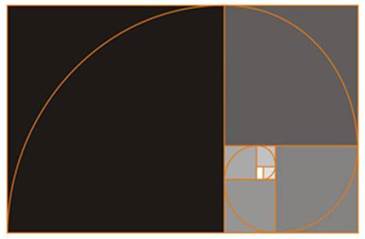 золотая логарифмическая спираль
золотая логарифмическая спираль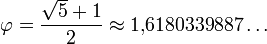
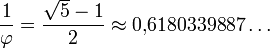
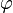 называется также золотым числом.
называется также золотым числом. задана рекурентним співвідношенням другого порядку
задана рекурентним співвідношенням другого порядку








