
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные обозначения геометрических объектовСодержание книги
Поиск на нашем сайте НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Конспект лекций
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Самара Издательство СГАУ УДК СГАУ: 514 (075) ББК 22.151.3 С 137
Рецензенты: докт. техн. наук, проф. Н.П. Крючин канд. техн. наук, доц. М.А. Петровичев
С 137 Савченко Н.В. Начертательная геометрия: Конспект лекций: учеб. пособие / Н.В. Савченко – Самара: Изд-во СГАУ, 2011. – 85 с.
ISBN 978 – 5 – 7883 – 0800 – 5
В настоящем учебном пособии кратко изложен теоретический материал курса начертательной геометрии. Пособие предназначено для использования студентами первого курса при подготовке к практическим занятиям и экзамену. Разработано для студентов механических факультетов, обучающихся по специальностям 160301 – Авиационные двигатели и энергетические установки, 160302 – Ракетные двигатели, 160201- Самолето- и вертолетостроение, 160801 – Ракетостроение, 160802 – Космические летательные аппараты и разгонные блоки.
ISBN 978 – 5 – 7883 – 0800 – 5
УДК СГАУ: 514 (075) ББК
© Н.В. Савченко, 2011
© Самарский государственный аэрокосмический университет, 2011
«Инженер, не умеющий чертить, подобен писателю, не умеющему писать».
А.Н. Туполев
Введение
Отличительной особенностью ускоряющегося научно-технического прогресса является экспоненциальный рост объема научно-технической информации. Наиболее эффективными средствами передачи информации являются визуальные. Знание этих средств, умение ими пользоваться – составляющие графической грамотности, основы которой в высшей школе закладываются при изучении курса «Начертательная геометрия». Следует отметить, что «Начертательная геометрия» включена в число обязательных дисциплин ведущих технических вузов мира. И связано это, прежде всего, с тем, что она как никакая другая дисциплина развивает логическое конструктивно-геометрическое мышление, пространственное представление и воображение, а также способность к анализу и синтезу пространственных форм. Основная задача начертательной геометрии – изучение визуально-образного геометрического языка и технологии его реализации. Она является уникальным техническим языком, информативность которого настолько велика, что заменить его другим практически невозможно. Роль ее в подготовке специалистов и решении прикладных задач возрастает в связи с необходимостью повышения эффективности труда конструктора. Основоположником этой графической науки был выдающийся французский математик и инженер Гаспар Монж, который в 1799 году издал свой классический труд под названием «Geometric descriptive» – «Начертательная геометрия». Основные положения этой книги не утратили своего значения и сегодня. Г. Монж дал достаточно четкое определение назначения начертательной геометрии, ее прикладного значения. Он отмечал, что начертательная геометрия дает возможность решать задачи с пространственными (трехмерными) объектами посредством графических построений, выполняемых на плоском чертеже, имеющем только два измерения. Начертательная геометрия учит нас, во-первых, строить и понимать технические чертежи, во-вторых, изучать по чертежу геометрические свойства изображаемых предметов, их форму, размеры. Исходя из этого, Г. Монж справедливо считал, что чертеж – это «язык техники». Более того, по его мнению, начертательная геометрия активно развивает интеллектуальные способности людей и тем самым создает возможность «совершенствования рода человеческого». С Монжем солидарны и многие отечественные ученые и конструкторы. В их числе известный русский геометр В.И. Курдюмов, который говорил, что если, по словам Монжа, считать чертеж языком техники, то начертательная геометрия является грамматикой этого языка. Греческий алфавит
Список рекомендуемой литературы Основная литература 1. Бубенников, А.В. Начертательная геометрия / А.В. Бубенников. – М.: Высшая школа, 1985. 2. Гордон, В.О. Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. – М.: Высшая школа, 1998. 3. Королев, Ю.И. Начертательная геометрия / Ю.И. Королев. – СПб: Питер, 2006. 4. Лагерь, А.И. Основы начертательной геометрии / А.И Лагерь, А.Н. Мота, К.С. Рушелюк. – М.: Высшая школа, 2005. 5. Локтев, О.В. Краткий курс начертательной геометрии / О.В. Локтев. – М.: Высшая школа, 1999. 6. Нартова, Л.Г. Начертательная геометрия / Л.Г. Нартова, В.И. Якунин. – М.: Дрофа, 2003. 7. Фролов, С.А. Начертательная геометрия / С.А. Фролов. – М.: Высшая школа, 2006. Дополнительная литература 8. Задания для графических работ по начертательной геометрии: метод. указания / сост. Л.П.Куванина, Л.А. Ратанова, Н.В. Савченко. – Самара: Изд-во СГАУ, 2007. 9. Начертательная геометрия. Примеры решения графических работ: метод. указания для студентов очно-заочной формы обучения / сост. Н.В. Савченко. – Самара: Изд-во СГАУ, 2007. 10. Начертательная геометрия. Примеры решения типовых задач и задания для контрольных работ: метод. указания для студентов-заочников. / Сост. Савченко Н.В.– Самара: Изд-во СГАУ, 2005. 11. Панин В.И. Геометрическое проектирование деталей самолета и двигателя в задачах по начертательной геометрии: учеб. пособие / В.И. Панин, М.И. Кочнев, К.И. Иващенко, Г.И. Панкова. – Куйбышев: Изд-во КуАИ, 1977. 12. Панин, В.И. Проецирование элементов авиационных двигателей в начертательной геометрии: учеб. пособие / В.И. Панин, М.И. Кочнев, К.И. Иващенко, Г.И. Панкова. – Куйбышев Изд-во КуАИ, 1978. 13. Пересечение многогранников плоскостью: метод. указания / сост. Л.П. Куванина, И.В. Мурачева. – Самара: СГАУ, 1992. 14. Пересечение поверхностей вращения плоскостью: метод. указания / сост. В.Я. Фадеев, Л.А. Ратанова – Куйбышев: КуАИ, 1991. 15. Пересечение прямой с поверхностью: метод. указания / сост. Г.И. Панкова. – Самара: КуАИ, 1991. 16. Применение основных теорем геометрии при решении задач по начертательной геометрии: метод. указания / сост. Н.Н. Калинина, В.И. Кулешова, СГАУ. – Самара, 2006. 17. Савченко, Н.В. Начертательная геометрия. Практические занятия: учеб. пособие / Н.В. Савченко, Г.И. Панкова, В.В. Платонова. – Самара: Изд-во СГАУ, 2007. 18. Савченко, Н.В. Сборник задач по начертательной геометрии. Часть 4. База данных: учеб. пособие / Н.В. Савченко [и др.]. – Самара: Изд-во СГАУ, 2011.
Лекция 1 ОСНОВЫ ТЕОРИИ ПОСТРОЕНИЯ ЧЕРТЕЖА Реальный предмет (деталь или сборочная единица) имеет трехмерную форму, которую необходимо передать на листе, имеющем лишь два измерения. Сделать это можно, зная законы построения изображений. Правила построения изображений в начертательной геометрии основываются на методе проецирования. Изображение предмета на плоскости (его проекция) строится с помощью проецирующих лучей. Виды проецирования Аппарат проецирования включает в себя проецируемый объект, проецирующие лучи и плоскость, на которую осуществляется проецирование. Вид проецирования зависит от способа проведения проецирующих лучей. Общим видом проецирования является центральное проецирование. Проецирование называется центральным, если проецирующие лучи проходят через неподвижную точку, называемую центром проекций. Пусть в пространстве находятся произвольные точки А и В, которые необходимо спроецировать на плоскость P¢, используя центр проекций (полюс) S. Для этого из центра S проводятся проецирующие лучи, проходящие через заданные точки и пересекающие плоскость. На пересечении этих лучей с плоскостью проекций P¢ находятся проекции точек (рис.1.1).
Рис. 1.1 Центральное проецирование не удобно для измерений, поэтому применяется, в основном, для построений перспективных изображений (перспективы). Методы построения таких изображений подробно рассматриваются в разделе начертательной геометрии «Линейная перспектива», который не входит в состав нашего курса. Частным случаем центрального проецирования является параллельное проецирование. При выполнении данного вида проецирования считается, что центр проекций находится в бесконечности. Проецирование называется параллельным, если все проецирующие лучи проходят параллельно друг другу. Параллельное проецирование осуществляется при выполнении двух условиях: 1) задано направление проецирования 2) проецирование ведется на плоскость, непараллельную направлению проецирования.
Рис. 1.2 В зависимости от угла наклона проецирующих лучей к плоскости проекций параллельное проецирование может быть: 1) прямоугольное (ортогональное), когда проецирующие углы падают на плоскость проекций под прямым углом ( 2) косоугольное (аксонометрическое), если направление проецирования составляет с плоскостью проекций угол не равный 90°. Построение всех машиностроительных чертежей основывается на прямоугольном проецировании, поэтому в дальнейшем будет рассматриваться только этот вид проецирования. Лекция 2 Проецирование прямой
Рис. 2.5 Аксиома евклидовой геометрии гласит: «Через две точки проходит единственная прямая». В связи с этим построение проекций прямой линии на КЧ сводится к построению проекций двух точек ей принадлежащих. Построим проекции прямой d, которой принадлежат точки А и В. Спроецировав их на плоскости проекций, а затем соединив между собой одноименные проекции, получаем проекции прямой (рис.2.5).
Рис. 2.6 На КЧ прямая может быть задана проекциями двух точек (отрезком) или, на основании инвариантного свойства 2[1], непосредственно своими проекциями (рис. 2.5 б, 2.6). Следы прямых линий Точка пересечения прямой с плоскостью проекций называется следом прямой. На рисунке 2.7 приведены пространственная модель и КЧ прямой l, пересекающей три плоскости проекций, а следовательно, имеющей три следа: - горизонтальный - фронтальный - профильный след Очевидно, что фронтальная и профильная проекции горизонтального следа (H) прямой лежат на осях проекций 0х и 0y соответственно. Проекции фронтального (F) и профильного (P) следов прямой находятся аналогично.
Рис. 2.15 Прямые общего положения пересекают три плоскости проекции и имеют три следа; прямые уровня пересекают две плоскости проекций (имеют два следа); проецирующие прямые пересекают одну плоскость проекции. Лекция 3 Рис. 3.2
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная (
Рис. 3.3 Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Рис. 3.4 Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи. На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают. Линии уровня плоскости Линиями уровня плоскости называются прямые, лежащие в плоскости и параллельные одной из плоскостей проекций. Существуют три линии уровня плоскости: горизонталь плоскости, фронталь плоскости и профильная прямая плоскости. 1. Горизонталь плоскости – прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций.
Рис. 3.7 Признаки и свойства горизонтали плоскости: 1) все горизонтали плоскости параллельны друг другу; 2) фронтальный след горизонтали (точка F) принадлежит фронтальному следу плоскости; 3) горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.
Рис. 3.8 На рис. 3.8 приведена плоскость общего положения, заданная 2. Фронталь плоскости – прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.
Рис. 3.9 Признаки и свойства фронтали плоскости: 1) все фронтали плоскости параллельны друг другу; 2) горизонтальный след фронтали (точка H) принадлежит горизонтальному следу плоскости; 3) фронтальная проекция фронтали параллельна фронтальному следу плоскости. Если плоскость не задана следами, то построение фронтали плоскости начинают с построения ее горизонтальной проекции, идущей параллельно оси х (рис. 3.8). Т.к. фронталь принадлежит плоскости, то имеет с ней две общие точки – 2 и А. Имея их горизонтальные проекции 3. Профильная прямая плоскости – прямая лежащая в плоскости и параллельная профильной плоскости проекций (рис. 3.10). Признаки и свойства профильной прямой плоскости: 1) все профильные прямые плоскости параллельны друг другу; 2) фронтальный след профильной прямой (точка F) принадлежит фронтальному следу плоскости, а ее горизонтальный след (точка H) – горизонтальному следу плоскости; 3) профильная проекция профильной прямой параллельна профильному следу плоскости. Если плоскость не задана следами, то построение профильной прямой плоскости начинают с построения ее фронтальной или горизонтальной проекций, идущих перпендикулярно оси х (рис. 3.10).
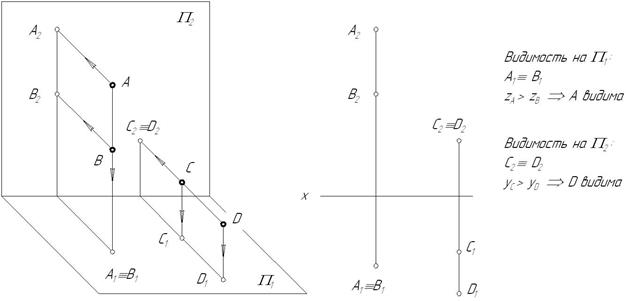
Рис. 3.10 Лекция 4 Определение видимости на КЧ Для улучшения наглядности изображений, заданных на КЧ, принято видимые для наблюдателя линии показывать сплошными, а невидимые – штриховыми линиями. При этом предполагается, что: 1) плоскости и поверхности непрозрачны; 2) луч зрения от наблюдателя всегда попадает перпендикулярно к той плоскости проекций, относительно которой определяется видимость. На рисунке 3.17 заданы две пары точек: 1) точки А и В, находящиеся на одном проецирующем луче, направленном перпендикулярно горизонтальной плоскости проекций 2) точки С и D, через которые проходит проецирующий луч, перпендикулярный фронтальной плоскости проекций
Рис. 3.17 Необходимо определить видимость точек относительно горизонтальной и фронтальной плоскостей проекций. Если на КЧ какие-либо две проекции точек совпадают, то для наблюдателя будет видима та точка, проекция которой находится дальше от оси проекций. Точки А и В, С и D называются точками, конкурирующими в видимости, а сам метод определения видимости – методом конкурирующих точек. Конкурирующими в видимости точками называются точки, лежащие на одном проецирующем луче, но принадлежащие разным геометрическим объектам. Лекция 5 Проецирование прямого угла В общем случае плоский угол проецируется на плоскость проекций с искажением. Возьмем две прямые общего положения l и k. Прямая l пересекает горизонтальную плоскость проекций под углом a, а прямая k – под углом a¢. Между собой прямые пересекаются под произвольным углом j. Прямоугольная проекция угла j1 определяется по формуле:
Рис. 4.1 Пусть
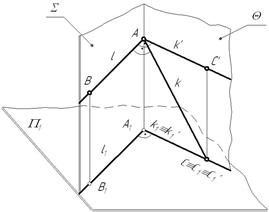
При Теорема о проецировании прямого угла: Прямой угол на плоскость проекций проецируется без искажения, если, по крайней мере, один из его лучей параллелен этой плоскости проекций. Пусть прямые l(АВ) и k(АС) пересекаются под прямым углом. Прямая l параллельна горизонтальной плоскости проекций. Тогда: 1. 2.
Рис. 4.2 Все прямые, лежащие в плоскости Пример: Построить перпендикуляр из точки А к горизонтали.
Рис. 4.3 Лекция 6 ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЙ. ЧЕТЫРЕ ОСНОВНЫЕ ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Для упрощения решения метрических, а также некоторых позиционных задач могут применяться методы, позволяющие переходить от задания фигур общих положений к частным. Эти методы основываются на двух принципах: 1) замещение системы плоскостей проекций на новую систему плоскостей, в которой неподвижный геометрический объект занимает какое-либо частное положение (способ замены плоскостей проекций); 2) перемещение геометрического объекта в пространстве таким образом, чтобы он занял какое-либо частное положение в неподвижной системе плоскостей проекций (способ вращения). В зависимости от расположения оси в пространстве, вокруг которой вращается геометрический объект, различают следующие виды способа вращения: 1) вращение вокруг линии уровня; 2) вращение вокруг проецирующей прямой; 3) плоско-параллельное перемещение. Эти способы преобразования включают в себя четыре основные задачи начертательной геометрии: 1. Преобразование комплексного чертежа таким образом, чтобы прямая общего положения стала линией уровня. 2. Преобразование комплексного чертежа таким образом, чтобы линия уровня стала проецирующей прямой. 3. Преобразование комплексного чертежа таким образом, чтобы плоскость общего положения стала проецирующей плоскостью уровня. 4. Преобразование комплексного чертежа таким образом, чтобы проецирующая плоскость стала плоскостью уровня. Лекция 7 Вращение точки
Рис. 5.7 Траектория движения точки – окружность (дуга окружности), центр которой находится на пересечении оси вращения с плоскостью вращения, а радиус вращения равен расстоянию от точки до оси. На КЧ траектория движения проецируется без искажения на ту плоскость проекций, к которой ось вращения перпендикулярна. На другие плоскости проекций она проецируется в виде отрезка, параллельного оси проекций. Вращение прямой Вращение прямой линии на КЧ сводится к вращению на один и тот же угол двух принадлежащих ей точек. Однако вращение прямой можно свести к вращению одной ее точки на заданный угол, если учитывать, что при вращении вокруг проецирующей оси проекция прямой на плоскость проекций, к которой эта ось перпендикулярна, остается равной самой себе. Возьмем отрезок АВ, принадлежащий прямой общего положения, и повернем его вокруг фронтально-проецирующей оси j так, чтобы он стал параллелен горизонтальной плоскости проекций (1 основная задача). На КЧ показана траектория вращения только одной точки, принадлежащей заданной прямой, находящейся на минимальном расстоянии от оси вращения.
Рис. 5.8 Если ось вращения на чертеже не задана, то ее можно выбрать таким образом, чтобы она пересекала прямую, тогда поворот вокруг нее значительно упрощается. На рис. 5.8 горизонтально-проецирующая ось вращения i пересекает горизонтальную прямую (A’B’). Тогда вращением вокруг нее одного из концов отрезка прямая преобразовывается в фронтально-проецирующую прямую (2 основная задача). Вращение плоскости Вращение плоскости вокруг проецирующей оси сводится к вращению на один и тот же угол элементов, определяющих эту плоскость в пространстве. Возьмем плоскость общего положения Чтобы найти натуральную величину плоской фигуры, следует провести второе вращение, преобразовав проецирующую плоскость в плоскость уровня (4 основная задача).
Рис. 5.9 Лекция 8 ПОВЕРХНОСТИ Поверхность – абстрактная фигура, не имеющая толщины. Она ограничивает какое-либо тело, состоящее из металла, пластмассы и т.д. Тело конечно, а поверхность может быть бесконечна. Например, шар ограничен сферой; боковой поверхностью конуса является коническая поверхность. 6.1. Способы задания поверхности Существует несколько способов задания поверхности, в том числе: кинематический, аналитический и графический. Внедрение в инженерную практику компьютерных технологий обусловило совместное использование графических и аналитических методов задания поверхностей. С точки зрения аналитической геометрии: Поверхность – непрерывное множество точек, координаты которых связаны в декартовой системе координат уравнением вида Если Если В начертательной геометрии поверхность задается графически, а к ее образованию подходят с точки зрения кинематики: Поверхность – совокупность непрерывных последовательных положений линий, движущихся в пространстве по определенному закону. Эта движущаяся линия называется образующей, а линия, по которой она движется, – направляющей. Поверхность считается заданной, если по одной проекции точки, принадлежащей ей, можно построить вторую проекцию. Совокупность независимых условий, необходимых и достаточных для однозначного определения поверхности, называется определителем поверхности:
где F – поверхность, (Г) – геометрическая часть определителя поверхности – совокупность геометрических фигур, образующих поверхность; [A] – алгоритмическая часть определителя поверхности – закон перемещения образующей.
Рис. 6.1
Например, определитель конической поверхности имеет следующий вид:
где l – образующая; а – направляющая; S – точка пересечения образующих. Алгоритмическая часть определителя читается следующим образом: Любая образующая l пересекает направляющую а и проходит через точку S.
На чертеже поверхность может быть задана: 1. Набором элементов, определяющих эту поверхность. 2. Очерком поверхности. 3. Каркасом поверхности. Очерком поверхности называется проекции контура поверхности на плоскости проекций. Каркасный способ задания поверхности предполагает, что поверхность можно определить как двупараметрическое множество точек с одной стороны, а с другой – поверхность – однопараметрическое множество линий. Каркасом (точечным или линейным) называется множество точек или линий, определяющих поверхность. Каркасным способом задаются такие сложные поверхности с образующими переменного вида, которые нельзя описать математически. Классификация поверхностей Существует множество различных подходов к классификации поверхностей. Однако главными из них являются следующие критерии: 1. Закон образования поверхности: - поверхности закономерные – если закон их образования известен и может быть выражен математически; - незакономерные. 2. Вид образующей: - поверхности линейные – образующая прямая линия; - поверхности нелинейные (криволинейные) – образующая кривая линия. 3. Закон движения образующей: - поверхности переноса – с поступательным движением образующей; - поверхности вращения – с вращательным движением образующей; - винтовые поверхности – с винтовым движением образующей. 4. Постоянность (вариабильность) формы образующей: - поверхности с образующей постоянной формы; - поверхности с образующей переменной формы. 5. Возможность развертывания поверхности: - развертываемые – поверхности, совмещаемые с плоскостью без складок и разрывов: - неразвертываемые. Очевидно, что любую поверхность можно классифицировать одновременно по нескольким признакам. Например, цилиндрическая поверхность вращения: 1) линейчатая закономерная развертываемая поверхность вращения; 2) циклическая поверхность переноса окружности постоянного радиуса; 3) алгебраическая поверхность второго порядка. Из всего множества поверхностей в кратком курсе начертательной геометрии мы будем рассматривать только гранные поверхности и поверхности вращения. Поверхности вращения Поверхности вращения имеют произвольную образующую, движущуюся по окружности. Каждая точка образующей l движется по окружности с центром на оси вращения i (рис. 6.4). Это окружность называется параллелью. Параллель, проходящая через наиболее удаленную от оси вращения точку образующей, называется экватором, а через ближайшую – горлом. Линия m, получаемая при пересечении поверхности плоскостью, проходящей через ось вращения, называется меридианом. Все меридианы поверхности вращения конгруэнтны. Каждый из них разделяется на два, симметричных относительно оси вращения, полумеридиана.
Рис. 6.4 Меридиан, лежащий в плоскости, параллельной плоскости проекций, называется главным меридианом. В данном примере он определяет фронтальный очерк поверхности, горизонтальный очерк определяется экватором и горлом. Цилиндр вращения
Рис. 6.5
Цилиндрическая поверхность вращения – поверхность, образованная движением прямой линии параллельно оси. Возьмем фронтально-проецирующий цилиндр и линию АВ, расположенную на его боковой поверхности. Горизонтальная проекция этой линии спроецируется на горизонтальный очерк цилиндра, т.к. все ее точки лежат на его боковой поверхности. Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности. Конус вращения Коническая поверхность вращения образуется движением прямой линии, пересекающей ось вращения.
Рис. 6.6 Точка принадлежит поверхности, если она принадлежит линии, лежащей на этой поверхности. Построение точек, принадлежащих поверхности вращения, ведется с помощью образующих или параллелей поверхности. Пусть задана фронтальная проекция точки А, принадлежащей поверхности конуса. Этой проекции соответствуют две горизонтальные проекции точки А1 и А¢1. Их можно определить с помощью образующих поверхности 1-S и 1¢-S или параллели p. Тор
Рис. 6.8 Точка А располагается на параллели внешней части открытого тора, точка В лежит на внутренней параллели. Поверхность тора образуется при вращении окружности вокруг оси, расположенной в плоскости окружности. В зависимости от соотношения величины радиуса образующей тора r и расстояния от центра окружности до оси вращения t возможны три разновидности тора (рис. 6.8): - образующая – окружность не пересекает ось вращения ( - образующая – окружность касается оси вращения ( - образующая – окружность пересекает ось вращения ( Лекция 9 Лекция 10 Развертка
Полная развертка боковой поверхности конуса представляет собой угол кругового сектора. Ее можно построить двумя способами:
1. Нахождение угла кругового сектора.
Рис. 6.16
где d – диаметр окружности основания конуса, l – длина образующей.
2. Способ малых хорд. Графическое построение величины Разрывать отсеченную боковую поверхность следует по наиболее короткой или длинной образующей, так чтобы развертка представляла собой симметричную фигуру и была единым целым.
Рис. 6.17 Пересечение поверхностей Пересечение многогранников Многогранники пересекаются по замкнутым пространственным ломаным линиям, которые могут быть найдены следующим образом: 1. Способ ребер. Находятся точки пересечения ребер одного многогранника с гранями другого. 2. Способ граней. Определяются отрезки прямых, по которым грани одного многогранника пересекаются с гранями другого. Пример: Построить линию пересечения двух трехгранных призм, одна из которых проецирующая. В результате пересечения заданных многогранников получается ломаная пространственная линии. Она соединяет соответствующие точки пересечения ребер одного многогранника с гранями другого. Так как одна из призм проецирующая относительно горизонтальной плоскости проекций, горизонтальная проекция линии пересечения совпадает с горизонтальным очерком этой призмы. Искомые точки сечения можно получить, решая задачу на пересечение прямой (ребра) с плоскостью (гранью).
Для построения точек пересечения ребра b с гранями призмы, используется горизонтально-проецирующая плоскость
Рис. 6.18 Для определения видимости линии сечения строится диаграмма, на которой схематично в произвольных размерах изображаются грани заданных призм. Знаками ²+² и ²-² отмечается видимость граней многогранников. На соответствующих гранях и ребрах наносятся точки сечения, и соединяют их с учетом видимости. Видимыми считаются те звенья линии пересечения, которые лежат на видимых гранях обоих многогранников. Лекция 11 Теорема 2: Если две квадрики имеют касание в двух точках, то линия их пересечения распадается на две коники, плоскости которых проходят через отрезок прямой, соединяющей эти точки.
Рис. 6.20
П
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.01 с.) |


 ;
;
 );
);

 ,
, ,
, .
.
 .
. ) и горизонтальная (
) и горизонтальная ( )проекции этой точки должны находиться на одной линии связи.
)проекции этой точки должны находиться на одной линии связи. .
.



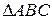 ,и принадлежащая ей горизонталь h. Если плоскость не задана следами, то построение горизонтали плоскости начинают с построения ее фронтальной проекции, идущей параллельно оси х. Т.к. горизонталь принадлежит плоскости, то она имеет с ней две общие точки – 1 и С. Зная их фронтальные проекции
,и принадлежащая ей горизонталь h. Если плоскость не задана следами, то построение горизонтали плоскости начинают с построения ее фронтальной проекции, идущей параллельно оси х. Т.к. горизонталь принадлежит плоскости, то она имеет с ней две общие точки – 1 и С. Зная их фронтальные проекции  и
и  , по линиям связи можно получить горизонтальные проекции
, по линиям связи можно получить горизонтальные проекции  и
и  ,а затем, соединив между собой, получить горизонтальную проекцию горизонтали.
,а затем, соединив между собой, получить горизонтальную проекцию горизонтали.
 и
и  и
и 
 ;
; .
.
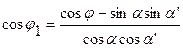 .
.
 ,
,  , тогда при
, тогда при  .
. .
. ,
,  , следовательно,
, следовательно,  .
.
 .
.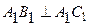 .
.
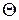 , на горизонтальную плоскость проекций проецируются перпендикулярно следу плоскости
, на горизонтальную плоскость проекций проецируются перпендикулярно следу плоскости  .
.


 и вращением вокруг проецирующей оси преобразуем ее в проецирующую плоскость (3 основная задача). Для этого преобразования необходимо провести одно вращение, при котором линия уровня плоскости превратится в проецирующую прямую.
и вращением вокруг проецирующей оси преобразуем ее в проецирующую плоскость (3 основная задача). Для этого преобразования необходимо провести одно вращение, при котором линия уровня плоскости превратится в проецирующую прямую.
 .
. – многочлен n -й степени, то поверхность называется алгебраической поверхностью n -го порядка.
– многочлен n -й степени, то поверхность называется алгебраической поверхностью n -го порядка. ,
,
 ,
,



 ) – открытый тор;
) – открытый тор; ) – закрытый тор;
) – закрытый тор; ) – закрытый тор.
) – закрытый тор.
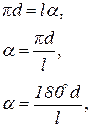
 осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.
осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.
 ,
,  .
. ,
,  .
.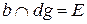 .
. .
.




