
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спираль Дюрера и «золотые» треугольникиСодержание книги
Поиск на нашем сайте
Обозначим большую сторону "золотого" прямоугольника через а, а короткую через х. Если от "золотого" прямоугольника отсечь квадрат, остается прямоугольник, большая сторона которого равна х, а малая а-х (рис. 7г). Отношение его сторон Если отсечь от оставшегося прямоугольника квадрат, от оставшегося прямоугольника снова отсечь квадрат и т.д., то получится бесконечная последовательность квадратов, стороны которых уменьшаются в геометрической прогрессии. В пределе они заполнят весь первоначальный квадрат, сойдясь в точке, которая называется полюсом золотого прямоугольника. В этой точке пересекаются диагонали золотых прямоугольников. На рисунке 7г изображена спираль, метод построения которой предложен Дюрером, – в каждый квадрат «золотого» прямоугольника вписывается четверть круга. Эта спираль имеет бесконечное количество витков, закручиваясь вокруг полюса золотого прямоугольника. Такая спираль проста в построении и часто встречается в различных орнаментах. Она же может использоваться для приближенного построения спиралей, встречающихся в ионическом ордере. В творениях и древних мастеров, и мастеров Возрождения часто просматриваются геометрические фигуры, пропорции которых связаны с "золотым" отношением. В "золотой" прямоугольник вписывается фасад Парфенона. Из двух отрезков, длины которых относятся в «золотой» пропорции можно построить треугольники, которые часто служили основой для определения пропорций архитектурных и художественных произведений. Замечательными свойствами обладает равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равно Ф (или отношение длины основания к длине боковой стороны равно j). Для того, чтобы построить такой треугольник, построим "золотой" прямоугольник, затем строим треугольник по его 3 заданным сторонам. В качестве основания берем короткую сторону прямоугольника, а боковые стороны равны длинной стороне прямоугольника (рис. 8а,б). Некоторые исследователи считают, что этот треугольник лежит в основе пропорции портрета Моны Лизы (рис. 8в). Углы этого треугольника при основании равны 72°, а угол, противолежащий основанию, равен 36°. Покажем, что отношение основания к боковой стороне равнобедренного треугольника, углы которого равны 72°, 72° и 36°, есть "золотое" число j. Проведем биссектрису AD угла А при основании (рис. 8а). Биссектриса разобьет треугольник АВС на 2 треугольника – ABD и ADC. Полученные треугольники равнобедренные. У треугольника AВD углы равны 36°, 36° и 108°. Следовательно, BD=AD=AC. У треугольника ADC углы равны 72°, 36° (половина угла в 72°) и ÐADC, равный 180°-72°-36°=72°. То есть, треугольник ADC – равнобедренный и длина биссектрисы угла при основании равна длине самого основания. Он подобен первоначальному треугольнику АВС (они имеют одинаковые углы). Из подобия этих треугольников следует, что:
Таким образом, отношение длины боковой стороны треугольника, углы которого равны 72°, 72° и 36°, к длине основания есть "золотое" число Ф (положительный корень), отношение длины меньшей стороны к длине большей равно j и конец биссектрисы делит боковую сторону в "золотом" отношении 1:j=Ф:1 (рис. 8а).
"Золотая" пропорция и правильные многоугольники Выпуклый n-угольник, чьи стороны и углы равны, называется правильным n-угольником. Научившисьделить окружность на n равных частей, мы научились строить правильные многоугольники. В правильный многоугольник можно вписать окружность. Вокруг него можно описать окружность. Точка, равноудаленная от вершин и сторон многоугольника, называется его центром. Он служит одновременно центром вписанной и описанной окружности.Угол, под которым видна сторона многоугольника из его центра, называется центральным. Центральный угол a правильного n-угольника равен Приведем значения величины центрального и внутреннего угла правильного многоугольника для наиболее часто встречающихся многоугольников (рис.9).
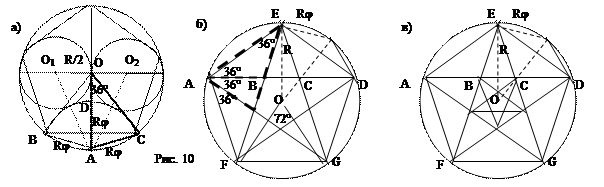
Сторона правильного десятиугольника, вписанного в окружность радиуса R, равна Rj (рис. 9). Действительно, центральный угол десятиугольника равен 36°. Сторона правильного десятиугольника является основанием равнобедренного треугольника, боковые стороны которого равны радиусу описанной окружности R. У этого треугольника углы при основании равны (180°-36°):2=72°. Такой треугольник мы только что описали. Его основание в j раз короче боковой стороны, равной R, то есть его длина равна Rj. Отсюда получаем способ деления окружности на 10 частей. В окружности радиуса R с центром О проводим вертикальный и горизонтальный диаметры. На горизонтальном диаметре располагаем центры 2-х окружностей радиуса R/2 (рис. 10а). Окружность с центром А, касающаяся окружностей О1 и О2, делит точкой D отрезок ОА в "золотом" отношении (см. рис. 7б), то есть AD=AB=AC=Rj.
Таким образом, равнобедренный треугольник АОС имеет стороны R, R и Rj и он подобен "золотому" треугольнику, углы которого равны 72°, 72° и 36° и его основание АС является стороной правильного многоугольника, число сторон которого находим из соотношения 360°:n=36°, то есть n=10, а хорда ВС – сторона правильного пятиугольника. Соединив через одну вершины десятиугольника с помощью прямых, получим правильный пятиугольник, а соединив через одну вершины пятиугольника - пятиконечную звезду (рис. 10б). Правильный пятиугольник и построенная на его основе пятиконечная звезда порождают знакомые уже нам равнобедренные "золотые" треугольники (на чертеже отмечены жирной штриховкой). Действительно, три угла с вершиной А равны друг другу, так как опираются на равные дуги. Следовательно, каждый из них равен 108°:3=36°. Аналогично равны 36° все остальные углы между стороной пятиугольника и лучом звезды или между двумя лучами звезды. В силу равенства длин лучей звезды все треугольники, две стороны которых лучи звезды, – равнобедренные. Таким образом, AD:AC=AC:CD=AB:BC=AD:AE=AE:EC=…=Ф. Из приведенной пропорции можно вывести следующие соотношения для сторон пятиугольников и лучей звезд. Например, примем длину ВС за 1. Тогда АВ=CD=Ф, AE=Ф2,… Продолжая ребра пятиугольника, можно получить еще одну пятиконечную звезду, затем еще одну и т.д. – целую последовательность разбегающихся наружу звезд и пятиугольников. Соединяя между собой через одну вершины пятиугольников, получим последовательность звезд, сходящихся к центру окружности.
«Золотая» прогрессия. «Золотые» модулеры В силу подобия бесконечная последовательность пятиконечных звезд порождает бесконечную последовательность отрезков, длины которых образуют геометрическую прогрессию с множителем Ф. Продолжение процесса внутрь, соответственно, порождает бесконечную геометрическую прогрессию с множителем …jn,…, j3, j2, j, 1, Ф, Ф2, Ф3,…, Фn,… и в числовой форме: …0,090; 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854;… Мы получили бесконечную последовательность, в которой каждый член больше предыдущего в Ф раз. В силу соотношения Ф2=1+Ф эта последовательность обладает следующим свойством: каждый ее член равен сумме 2-х предшествующих ему членов - если мы, начиная с любого места, перенумеруем члены последовательности и присвоим им обозначения un, то un=un-1+un-2. Действительно, un-1=un-2Ф и Ф2=1+Ф, следовательно: un-1+un-2=un-2Ф+un-2=un-2(1+Ф)=un-2Ф2=un. Свойство un=un-1+un-2 позволяет, не прибегая к вычислениям, строить все члены этой последовательности, если известны значения только 2-х любых соседних членов. Например, мы знаем значения u1=1 и u2=Ф. Значения следующих членов: u3=Ф2=1+Ф, u4=Ф3=u2+u3=Ф+Ф2,… Построим шкалу, основанную на "золотой" пропорции, выбрав в качестве единичного некоторый, вообще говоря произвольный, отрезок. Для этого проведем горизонтальную прямую и отметим на ней точки А1, А2, А3,…, расстояния между которыми равны 1, Ф, Ф2,… Для того, чтобы построить отрезок длины Ф2 достаточно сложить отрезки длины 1 и Ф. Для того, чтобы построить следующий отрезок, надо сложить отрезки Ф и Ф2 и т.д. А1А2:А2А3:..=В1В2:В2В3:..=С1С2:С2С3:..=М1М2:М2М3:М3М4… Эту шкалу можно настроить на любую единицу измерения. Для этого надо через точки, отмечающие деления шкалы, провести пучок прямых с центром V (рис. 11а). Эти прямые, пересекая горизонтали, порождают новые шкалы. Эти шкалы в силу теоремы о подобных треугольниках будут также основаны на "золотой" пропорции, но с единичным отрезком другой длины.
Подобрав горизонталь так, чтобы М1М2 был равен отрезку, который мы хотим иметь в качестве единичного, и проведя через его конец горизонтальную прямую, получим "золотую" шкалу с выбранным нами единичным отрезком (рис. 11). Задача, которую помогает решить построенный нами универсальный "золотой" модулер. Задан отрезок, разделенный в некотором отношении. Является ли это отношение "золотым"? Решение. Найдем уровень, на котором левый конец заданного отрезка касается вертикали, а правый касается прямой VA3. На рисунке 11 отрезок в этом положении выделен более жирным окрасом. Если точка N2 попадает на прямую VA2, то деление – в "золотом" отношении. На нашем рисунке показано, что отношение очень близко к "золотому". Справа на рисунке 11 изображен золотой модулер, содержащий последовательность отрезков, длины которых образуют геометрическую прогрессию с множителем j=0,618. В качестве упражнения проставьте выражения для этих длин на рисунке. Стороны пятиугольника и десятиугольника, вписанные в одну и ту же окружность радиуса R, связаны соотношением: а52=R2+a102. То есть сторона пятиугольника равна гипотенузе прямоугольного треугольника, катеты которого равны R и Rj, и
Это позволяет с помощью теоремы о подобных треугольниках по заданной стороне пятиугольника получить радиус описанной окружности. Для этого достаточно построить любой «золотой» прямоугольник, на прямой, соединяющей его вершины, расположенные на диагонали, отложить требуемую длину стороны пятиугольника и опустить перпендикуляр на горизонталь (рис. 12а). Полученный горизонтальный отрезок - радиус окружности, с помощью которой надо строить пятиугольник. А можно просто построить любой правильный пятиугольник и увеличить его до нужного размера с помощью гомотетии (рис. 12б). Аналогично можно, применив принцип подобия, использовать в качестве "золотого" модулера половину "золотого" прямоугольника - прямоугольный треугольник со сторонами 1 и Ф. Если отложить по горизонтали некоторый отрезок, то вертикаль, восставленная из конца отрезка до пересечения с гипотенузой будет иметь длину в Ф раз меньшую. А можно по длине вертикали найти длину горизонтали в Ф раз большую (рис. 12в). Архитекторы с давних времен для получения отрезков, находящихся в заданном пропорциональном соотношении, пользуются пропорциональным циркулем. Он состоит из двух равных по длине ножек, скрепленных винтом (рис. 12г). Если винт разбивает ножки в отношении a:b, то в таком же отношении будут находиться измеряемые им отрезки c и d: При раскопках найдено по крайней мере четыре пропорциональных циркуля, - Помпейский пропорциональный циркуль с соотношением 90:56»1.607, 2 пропорциональных циркуля с соотношением 2:1, пропорциональный циркуль из Музея Терм в Риме с соотношением 94:52»1.807 (как
Производные «золота» Самое простое разбиение отрезка на две части - это деление отрезка точно пополам. Некоторое смещение от центра отрезка точки деления отрезка на две части улучшает зрительное впечатление. Эта цель достигается с помощью деления в "золотой" пропорции. Обмеры показали, что для того, чтобы смягчить слишком резкое отклонение золотого сечения от точного деления пополам, мастера применяли золотое сечение повторно, что приводило к делению отрезка в пропорции Если еще раз выполнить золотое сечение отрезка, получится деление отрезка в пропорции 507:493»1,028. Следующее сечение, дающее деление отрезка в пропорции 501:499»1,004, практически неотличимо от точного деления отрезка пополам (все эти значения выражаются через рациональные функции, зависящие от
Если архитектор выбирает для себя некоторый способ гармонизации, то ему нужен циркуль, настроенный на выбранную пропорцию. Циркуль без изменения раствора позволяет построить 3 отрезка (рис: 14). Три отрезка, построенных циркулем, настроенным на "золотую" пропорцию, обеспечивают одинаковое пропорциональное деление целого и части.
Очень интересными свойствами обладает прямоугольный треугольник, у которого "золотым" является отношение гипотенузы к меньшему катету (рис. 15а). Если а - длина меньшего катета, то согласно теореме Пифагора и соотношению Ф2=1+Ф, его второй катет равен
Пропорции
Ниже, мы еще раз встретимся с
Задачи для самостоятельного решения. 1. Построить с помощью циркуля и линейки нормальный полиграфический прямоугольник. 2. Построить с помощью циркуля и линейки рядом с одним квадратом другой квадрат, площадь которого вдвое меньше. 3. Для измерения высоты дерева в землю воткнули шест длиной 2м и измерили длину тени от шеста (3м) и от дерева (15м). Какова высота дерева? 4. Разрез Пантеона в Риме (II в.н.э.) приведен на чертеже в масштабе 20мм – 20м. Диаметр круга на чертеже равен 4,3см (рис. 16). Найти высоту стен и купола.
5. Выписать 12 первых членов последовательности чисел Фибоначчи. 6. Построить с помощью циркуля и линейки 7. Построить "золотой" прямоугольник по большой стороне. 8. Построить "золотой" прямоугольник по малой стороне. 9. Построить спираль Дюрера 10. Построить "золотой" прямоугольный треугольник. 11. Построить "золотой" равнобедренный треугольник (углы которого равны 72°, 72° и 36°. 12. Построить последовательность отрезков, длины которых находятся в пропорциональном отношении 1:Ф:Ф2:Ф3… 13. Вычислить первые 5 членов геометрической прогрессии: 1, 14. Построить последовательность отрезков, длины которых находятся в пропорциональном отношении 1: 15. Построить правильный пятиугольник по заданной стороне. 16. Построить 5 концентрических окружностей, расстояния между которыми суть геометрическая прогрессия с множителем Ф. Поделить окружности на 16 равных частей. Получившуюся сетку использовать для построения рисунка из спиралей. 17. По репродукции пейзажа с линией горизонта определите, делит ли линия горизонта картину по высоте в «золотом» отношении. 18. Для прогрессии r2, r4, r6,…, для которой выполняется 19. Для прогрессии r, r3, r5, r7,…, для которой выполняется Глава 5
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.008 с.) |

 в силу соотношения
в силу соотношения  равно соотношению сторон
равно соотношению сторон  в первоначальном прямоугольнике. То есть новый прямоугольник подобен первоначальному.
в первоначальном прямоугольнике. То есть новый прямоугольник подобен первоначальному. . Кроме того, ВС=BD+DC=AD+DC=AC+DC и, следовательно, DC=ВС-АС. Введем обозначения: АС= а, АВ= k и подставим эти значения в пропорцию:
. Кроме того, ВС=BD+DC=AD+DC=AC+DC и, следовательно, DC=ВС-АС. Введем обозначения: АС= а, АВ= k и подставим эти значения в пропорцию:  . Обозначим
. Обозначим  , и решаем уравнение:
, и решаем уравнение: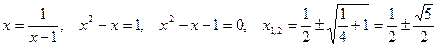

 . Угол при вершине называется внутренним углом многоугольника. Величина углов, опирающихся на одну и ту же дугу окружности, вершина одного из которых – центр окружности (центральный угол, его величина a), а вершина другого лежит на окружности (такие углы называются вписанными, его величина b), связаны соотношением: b=a/2. Величина внутреннего угла b вычисляется по формуле:
. Угол при вершине называется внутренним углом многоугольника. Величина углов, опирающихся на одну и ту же дугу окружности, вершина одного из которых – центр окружности (центральный угол, его величина a), а вершина другого лежит на окружности (такие углы называются вписанными, его величина b), связаны соотношением: b=a/2. Величина внутреннего угла b вычисляется по формуле:  . Действительно, центральный угол, соответствующий внутреннему углу правильного многоугольника, состоит из n-2 углов размером 360°/n. Откуда и получается приведенная формула.
. Действительно, центральный угол, соответствующий внутреннему углу правильного многоугольника, состоит из n-2 углов размером 360°/n. Откуда и получается приведенная формула.
 . Выпишем эту прогрессию в виде:
. Выпишем эту прогрессию в виде:
 (R≈0,85a5). Тем самым, она равна диагонали "золотого" прямоугольника, у которого большая сторона равна радиусу окружности, в которую вписан пятиугольник.
(R≈0,85a5). Тем самым, она равна диагонали "золотого" прямоугольника, у которого большая сторона равна радиусу окружности, в которую вписан пятиугольник.
 .
.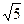 :(
:( , которую с точностью до 3-х знаков можно описать рациональным соотношением 528:472»1,118. Это отношение называют производной золотого сечения (рис.13).
, которую с точностью до 3-х знаков можно описать рациональным соотношением 528:472»1,118. Это отношение называют производной золотого сечения (рис.13).

 . То есть длины его сторон образуют геометрическую прогрессию 1, q, q2 с множителем q=
. То есть длины его сторон образуют геометрическую прогрессию 1, q, q2 с множителем q=  . Для примера на рисунках 15б,в продемонстрированы фигуры, которые можно построить с помощью треугольников такого вида (
. Для примера на рисунках 15б,в продемонстрированы фигуры, которые можно построить с помощью треугольников такого вида (
 Спираль из дуг, построенная вокруг улитки
Спираль из дуг, построенная вокруг улитки 



 «Троица» Рублева и золотые пропорции
«Троица» Рублева и золотые пропорции

 , найти значение r.
, найти значение r. , найти значение r.
, найти значение r.


