
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площади боковых поверхностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для пирамид боковая поверхность вычисляется по формуле площадей треугольников, у которых высотой являются перпендикуляры, опущенные из вершины на стороны основания (ее мы даже не приводим). Площадь боковой поверхности S круглого прямого конуса c образующей l и радиусом основания r вычисляется по формуле: S=p rl. Для того чтобы понять, почему это так, развернем конус и положим его на плоскость (рис. 12а). Для конуса (в отличие от шара) эта операция возможна, конус состоит из прямолинейных образующих. Разрежем всю поверхность, разложенную на плоскости, на много узеньких секторов. Каждый сектор – почти треугольник. Для площади треугольника SΔ-ка имеет место формула SΔ-ка=1/2hD, где D - основание треугольника, а h – его высота. Площадь конуса равна сумме площадей всех треугольников, на которые он разбит.
Для вычисления боковой поверхности, а также объема наклонного цилиндра, можно воспользоваться двумя формулами – одна зависит от образующей и сечения, перпендикулярного к образующей, другая – от основания и высоты: S=ph=sl (p – периметр основания, h – высота, s – периметр сечения, перпендикулярного к образующей, l – образующая) V=Fh=Ql (F – площадь основания, Q – площадь сечения, перпендикулярного к образующей Площадь поверхности шара S=4pr2. Шар развернуть на плоскости нельзя. Поэтому для шара нельзя провести такие же рассуждения, какие мы провели для конуса и цилиндра, и для него формулу S=4pr2 мы выведем с помощью других рассуждений. Построим проекцию шара на плоскость следующим образом. Опишем вокруг шара круговой цилиндр того же радиуса и будем проектировать точки шара на поверхность цилиндра при помощи прямых, перпендикулярных к цилиндру. Если разрезать цилиндр вдоль одной из образующих и развернуть его на плоскости, то мы получим изображение шара на плоскости, обладающее тем замечательным свойством, что оно сохраняет площади (хотя и искажает изображение). Показав это, мы заодно выведем формулу для площади поверхности шара.
Доказательство достаточно провести для "бесконечно малых" кусков поверхности шара. В силу круговой симметрии шара в качестве таких кусков можно взять поверхности узких круговых сегментов шара. Возьмем такой сегмент на широте a (a - угол радиуса с горизонтальной плоскостью – см. рис. 13а). Его площадь S=2prDs, где r – радиус сегмента, Ds – длина куска меридиана. Для "широты" a r=Rcosa, а Ds=Dh/cosa. Таким образом, S=2pRDh, и этой же величине равна площадь полоски на цилиндре, которая является проекцией сегмента. Следовательно, площади сегмента и его проекции равны друг другу, а площадь всего шара равна боковой поверхности цилиндра, образующая которого равна 2R, то есть она равна 2R×2pR=4pR2 (рис. 13б). Заодно мы получили формулу величины боковой поверхности любого сегмента шара S. Она равна 2pRh, где R – радиус шара, а h – высота сегмента (рис. 13в). Таким образом, величина боковой поверхности сегмента зависит только от его высоты и, конечно, от радиуса шара. Можете ли вы решить задачу из рукописи XVII века?
Задачи для самостоятельного решения 1. Чему равен в миллиметрах диаметр пули трехлинейной винтовки (3 линии)? 2. Скольким центнерам с гектара соответствует урожай 30 пудов с десятины? 3. Скорость ветра 30м/сек. Чему она равна в единицах км/час? 4. Для египетской пирамиды, имеющей основание 232´232 и угол наклона боковой грани 52° найти высоту, длину бокового ребра и его угол с основанием. 5. Для египетской пирамиды, имеющей основание 70´70 и высоту 50 найти угол наклона боковой грани, длину бокового ребра и его угол с основанием. 6. Высота египетской пирамиды 52м, длина ребра78м. Найти величину основания и угол наклона боковой грани пирамиды. 7. Длина стороны основания пирамиды 67м, высота 44м. Найти длину ребра пирамиды и угол наклона ее боковой грани. 8. У одуванчика, выросшего в тени, длина листа оказалась 33см, а у одуванчика, выросшего на солнцепеке – 3,3см. Во сколько раз площадь первого листа больше площади второго? Аналогично, если длина одного листа на 40% превосходит длину подобного ему листа, то во сколько раз различаются их площади? 9. Радиус железнодорожного закругления 800м. Длина рельсового пути на нем 60м. Сколько градусов в дуге закругления? 10. Яйцо страуса длиннее куриного в 2,5 раза. Во сколько раз больше его объем? 11. Какой объем в кубометрах и куб. саженях занимает куча щебня, имеющая коническую форму, если окружность ее основания равна 12,1м, а длина двух образующих – 4,6м (измерено с помощью веревки, перекинутой через вершину конуса). Чему равен тангенс угла наклона и какой (приблизительно) угол наклона образующей с горизонталью (воспользоваться таблицей тангенса; для определения высоты кучи воспользуйтесь теоремой Пифагора). 12. Найти объем ведра, диаметр дна которого 20см, верхний диаметр 30см, образующая 25см. 13. Найти размер поверхности крыш и маковок, изображенных на рис. 14.
14. Катеты прямоугольного треугольника равны 3 и 4. Найдите радиус описанной окружности, углы и тригонометрические функции углов этого треугольника. 15. Сторона АВ в треугольнике АВС равна 3, ÐВАС=60°, ÐАВС=75°. Найти ВС. 16. Найдите косинусы углов треугольника со сторонами 5, 6 и 7. 17. В треугольнике АВС угол при вершине А равен 60°, АВ=3, АС=4. Найти ВС. 18. В треугольнике АВС углы А и В равны соответственно 60° и 75°. Чему равно отношение сторон АВ и АС?
Глава 8 Метод координат До сих пор мы изучали свойства фигур, связанные только с их размерами и формой, и рассматривали простейшие преобразования фигур, состоящие в движении или растяжении. Мы занимались геометрией. Для того чтобы научиться описывать достаточно сложные геометрические объекты и строить изображение на плоскости некоторых пространственных объектов, очень помогает привлечение алгебраического аппарата. Алгебра и геометрия на самом деле очень близки. Установление связи между алгеброй и геометрией стало, по существу, революцией в математике. Переводить геометрические образы на язык алгебры, то есть уравнений, позволяет метод координат, введенный основоположником аналитической геометрии французским математиком Рене Декартом, жившим в XVII веке. Метод координат состоит в том, что в рассматриваемом пространстве определяется система координат и тогда положение любой точки М однозначно определяется заданием чисел – ее координат в этой системе координат. На плоскости – это пара чисел. В пространстве – тройка чисел. Система координат устанавливает взаимно однозначное соответствие между точками и их координатами. Она позволяет создать геометрический образ уравнений и неравенств, и, наоборот, геометрические образы описать средствами систем уравнений и неравенств. Рассмотрим наиболее часто употребляющиеся системы координат.
Декартовы координаты Декартова прямоугольная система координат на плоскости задается следующим образом. Через точку О проводятся две взаимно-перпендикулярные прямые. Одна называется осью X, другая осью Y. Как на оси X, так и на оси Y задается масштаб – какой-либо отрезок принимается за единицу. Тогда для любой точки плоскости М определены ее декартовыкоординаты. Чтобы их найти, проведем через точку М прямую, параллельную оси Y. Расстояние от точки пересечения этой прямой с осью X до начала координат О есть первая координата точки М - х. Проведем через точку М прямую, параллельную оси X. Расстояние от точки пересечения этой прямой с осью Y до начала координат О есть вторая координата точки М - у. Число x называют абсциссой, а y - ординатой точки М (рис.1а). И наоборот. Две координаты x и y определяют единственную точку плоскости. Чтобы ее найти, надо на оси x от точки О отложить величину x и провести через эту точку прямую, параллельную оси Y. На оси Y от точки О отложить величину y и провести через эту точку прямую, параллельную оси X. Точка пересечения этих прямых М имеет координаты x и y. Легко видеть, что такой способ определения координат устанавливает взаимно однозначное соответствие между точками и парами чисел – координатами. В приведенной на рисунке 1 системе координат ось Y получается из оси Х поворотом против часовой стрелки. Такая система координат называется правой. В левой системе координат ось Y получается из оси Х поворотом по часовой стрелке. Если в правой системе координат точка имеет координаты (x,y), то в левой системе координат такие координаты будет иметь ее зеркальное отражение (рис.1а,б). Принято пользоваться правой системой координат. Понятие правого и левого направления может оказаться важным при изготовлении копий. Например, надо учитывать, что если на доску нанесен рисунок, отпечаток с него, полученный наложением, даст его зеркальное отражение.
При построении системы координат можно было бы взять оси, не ортогональные друг другу. Это не нарушило бы рассуждений об однозначном соответствии между точками и парами чисел, их координатами в такой системе. Ведь мы нигде не пользовались тем обстоятельством, что оси координат ортогональны друг другу. Такая система координат называется косоугольной ( рис. 1в ). Система координат, оси которой ортогональны друг другу, называется прямоугольной. Декартова система координат (прямоугольная, правая) является самой простой и часто используемой координатной системой. Расстояние r между двумя точками M1(x1,y1) и M2(x2y2) (рис. 1г) в прямоугольной системе координат согласно теореме Пифагора равно:
Векторы на плоскости Рассмотрим на плоскости две точки А и В. Обозначим через Длина вектора Для любого вектора вектор Суммой двух векторов расположим векторы Правило сложения векторов можно сформулировать иначе, в виде правила параллелограмма: пусть начала векторов Разностью векторов
Рассмотрим декартову систему координат. Обозначим через Возьмем произвольный вектор Легко видеть, что если
Аналогично координаты суммы векторов равны сумме координат слагаемых (рис. 3в). Пусть
Примеры 1. Заданы 2 вектора Решение. x=3-2=1, y=0-0=0, 2. К точке приложены 4 силы, их направление и величина изображены на рисунке 4б (если соединить концы векторов, то получится параллелограмм). Чему равна равнодействующая всех сил? Решение. Равнодействующая равна нулю, так как силы, направление которых совпадает с направлением одной и той же диагонали, равны по величине, но противоположны по направлению. 3. Угол между двумя равными по величине векторами Решение приведено на рисунке 4в: |
Полярная система координат Приведем пример еще одной системы координат на плоскости, тоже достаточно простой и в некоторых случаях более удобной, чем декартова система. Пусть на плоскости даны некоторая точка О и проходящая через нее ось ОР. Точку О будем называть полюсом. А ось ОР – полярной осью. Положение любой точки М плоскости определяется расстоянием r этой точки от полюса и полярным углом φ между полярной осью и радиусом-вектором точки. Величина радиуса-вектора r и полярного угла φ будут координатами точки (рис. 5). Две координаты – r и φ определяют единственную точку плоскости. Действительно, эту точку, зная r и φ, можно найти с помощью следующей процедуры. Опишем вокруг точки О окружность радиуса r. Возьмем тот ее радиус, угол между которым и полярной осью ОР равен φ. Координаты точки пересечения этого радиуса и окружности r и φ (рис. 5).
Такая система координат называется полярной. А координаты r и φ – полярными координатами. Принято считать, что φ принимает значения от нуля до 2p, а значение r всегда положительно. Заметим, что величина радиуса-вектора полюса О равна нулю, а его полярный угол не определен. Угловые координаты удобно применять в тех случаях, когда важным параметром является направление на плоскости. Например, угловую полярную систему координат на плоскости задает компас, стрелка которого указывает всегда на север. Центр системы находится там, где находится наблюдатель. Шкала компаса делится на 360°. Грубые ориентиры – направления на восток (90°), юг (180°) и запад (270°). При отсутствии компаса для определения направления можно, пользуясь часами и знанием правил пропорций, ориентироваться по солнцу. Примеры 1.Примем, что солнце бывает на востоке в 6 часов утра, на юге в 12 час дня, на западе в 6 часов вечера. На каком направлении находится солнце а) в 3 часа дня, б) в 10 часов утра, в) если нам надо идти на юг, а сейчас 9 часов утра, какой угол должно составлять наше направление с направлением на солнце?
а) б) с)
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.237.229 (0.012 с.) |

 , где h≈l, а s=2πr – приблизительно длина периметра основания. Чем больше число секторов, тем ближе h к величине l, а s - к периметру основания. Так что в пределе получим нужную формулу. С помощью развертывания боковой поверхности на плоскости выводится и формула для вычисления площади боковой поверхности прямого цилиндра (образующая прямого цилиндра перпендикулярна плоскости основания). Если развернуть прямой цилиндр, то получится прямоугольник, откуда и получается формула: S= ls, где l – длина образующей цилиндра, а s – периметр основания (рис. 12б). Основание может иметь любую форму (строго говоря, основание должно быть измеримой фигурой). Если развернуть непрямой цилиндр, то получится параллелограмм с изогнутыми в виде синусоиды основаниями, а не прямоугольник. Его площадь зависит от угла наклона цилиндра, или его высоты (рис. 12в).
, где h≈l, а s=2πr – приблизительно длина периметра основания. Чем больше число секторов, тем ближе h к величине l, а s - к периметру основания. Так что в пределе получим нужную формулу. С помощью развертывания боковой поверхности на плоскости выводится и формула для вычисления площади боковой поверхности прямого цилиндра (образующая прямого цилиндра перпендикулярна плоскости основания). Если развернуть прямой цилиндр, то получится прямоугольник, откуда и получается формула: S= ls, где l – длина образующей цилиндра, а s – периметр основания (рис. 12б). Основание может иметь любую форму (строго говоря, основание должно быть измеримой фигурой). Если развернуть непрямой цилиндр, то получится параллелограмм с изогнутыми в виде синусоиды основаниями, а не прямоугольник. Его площадь зависит от угла наклона цилиндра, или его высоты (рис. 12в).

 ). Ответ: 352аршин.
). Ответ: 352аршин.


 =
=  вектор АВ, понимая под этим направленный отрезок АВ, т.е. отрезок, у которого точка А является началом, а точка В концом (рис 2а.).
вектор АВ, понимая под этим направленный отрезок АВ, т.е. отрезок, у которого точка А является началом, а точка В концом (рис 2а.). |. Вектор нулевой длины называется нулевым,его обозначение
|. Вектор нулевой длины называется нулевым,его обозначение  или просто 0.
или просто 0. = k
= k 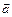 , являющийся произведением вектора
, являющийся произведением вектора  имеет то же направление, что и вектор
имеет то же направление, что и вектор  и
и  ).
). , полученный по следующему правилу:
, полученный по следующему правилу: будет начало вектора
будет начало вектора  (рис.2д).
(рис.2д).
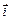 и
и  векторы единичной длины, направленные по осям координат.
векторы единичной длины, направленные по осям координат.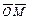 на координатные оси (рис. 3а). Имеем:
на координатные оси (рис. 3а). Имеем:  . Говорят, что х и y являются координатами вектора
. Говорят, что х и y являются координатами вектора 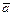 в этой системе координат и записывают это следующим образом:
в этой системе координат и записывают это следующим образом:  .
. (x',y') связан с вектором
(x',y') связан с вектором 
 =
=  . Тогда x3=x1+x2 и y3=y1+y2.
. Тогда x3=x1+x2 и y3=y1+y2.  , |
, | 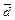 =
= 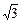 |
| 

 Решение. Рисунок 6 поможет понять решение. Будем руководствоваться тем, что расстояние в градусах между востоком и югом и между югом и западом равно 90°, а разница во времени для 90° градусов равна 6 часам.
Решение. Рисунок 6 поможет понять решение. Будем руководствоваться тем, что расстояние в градусах между востоком и югом и между югом и западом равно 90°, а разница во времени для 90° градусов равна 6 часам.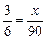 , х =45° - в 3 часа дня солнце на юго-западе (в 45° к югу от запада - 225°).
, х =45° - в 3 часа дня солнце на юго-западе (в 45° к югу от запада - 225°). , х =60° - в 10 часов утра солнце в 60° от востока к югу - 150°.
, х =60° - в 10 часов утра солнце в 60° от востока к югу - 150°.


