
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симметричные мозаики (паркеты)Содержание книги
Поиск на нашем сайте
Самая главная составная часть узора мозаики – это сеть. На клетки сети накладывается с ритмичным повтореним мотив узора, причем сама сеть в мозаике может остаться в составе узора или же ее после наложения мотива удаляют. Узор мозаики образуется из клеток схемы, сплошь заполняющих весь фон. Самые простые клетки, которые приходят в голову и самым неискушенным творцам, - знакомые всем паркеты из квадратных или прямоугольных плиток или полы в ванной, выложенные шестигранниками. Для улучшения впечатления внутри плиток располагают симметричный узор. За несколько тысячелетий существования человечества было создано бесчисленное количество мозаик. По названию формы клетки, по которой строится мозаика, их называют: параллелограммная, прямоугольная, ромбическая, треугольная, квадратная, шестиугольная мозаика («пчелиные соты») (рис. 16).
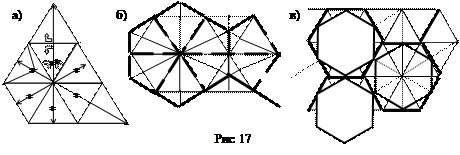
Желание создать что-то необычное, присущее людям искусства, заставляло искать способы построения мозаик на основе и других симметричных фигур, например, широко используемых в розетках правильных пятиугольников, восьмиугольников и т.д. Но никогда никому ни одной мозаики, в основе которой лежит правильный пятиугольник или правильный многоугольник, число сторон у которого больше 6, создать не удалось. Это является следствием главного отличия мозаики от розетки. Клетки мозаики должны заполнять пространство целиком. И оказалось, что необходимость целиком покрывать поверхность накладывает ограничения на кванты мозаики. Можно сказать, что творцы мозаик доказали практически, что такие мозаики, в основе которых лежит правильный многоугольник, число сторон у которого 5 или больше 6, невозможны. Только в ХХ веке математиками это было доказано теоретически. Было создано полное описание возможных схем мозаик на плоскости. С формальной точки зрения существует 17 различных типов мозаичных схем на плоскости. Из них 12 включают отражения, 5 – повороты и переносы [Гинзбург]. К чести создателей мозаик оказалось, что они не пропустили ничего. При создании мозаики сначала определяется вид сети, по которой будет строиться мозаика, и строится соответствующая решетка. Не вызывает затруднений построение квадратной, ромбической, параллелограммной, треугольной решетки. В шестиугольной мозаике квантом служит правильный шестиугольник. Сплошная сетка из шестиугольников (пчелиные соты)встречается в природе. Для этого имеются веские основания - сеть, имеющая такую структуру, имеет минимум длины. Решетка из шестиугольников строится на основе решетки из треугольников. (рис. 14). Сеть состоит из квантов. При переходе от одного кванта к другому и построении узора внутри кванта могут применяться переносы, отражения и вращения (набор возможных углов поворота зависит от формы кванта). В параллелограммной мозаике используется перенос и перенос+поворот; в прямоугольной используются только отражение и перенос + отражение. В ромбической комбинируется и отражение, и поворот и перенос (целых 5 комбинаций; диагонали ромба взаимно перпендикулярны и делят углы ромба пополам – это дает дополнительные возможности); в треугольной – отражение и вращение (вокруг центра на 120°); в квадратной – отражение, вращение и отражение+вращение. Симметричная форма "пчелиных сот" предоставляет массу возможностей для создания симметричных орнаментов. На основе центров шестиугольников, центров входящих в них треугольников и всех осей симметрии создано множество узоров для покрытий полов и стен, ковров, дверей и т.д. Для того, чтобы в шестиугольной сетке построить все оси симметрии, надо дополнительно соединить прямыми центры всех соприкасающихся шестиугольников. На рисунке 17а приведена схема возможных движений для шестиугольной мозаики. Центр шестиугольника, все его вершины можно использовать для поворотов на 60°, 120° и 180°. Центры всех равносторонних треугольников (отмечены '*') – для поворотов на 120°. Прямые, соединяющие между собой центр и середину ребра, можно использовать в качестве линий отражения внутри шестиугольника, 6 ребер можно использовать в качестве линий отражения для распространения рисунка за пределы кванта, для получения следующего кванта (две стрелки вдоль линии, смотрящие в разные стороны). Для получения следующего кванта можно использовать перенос центра в вершину шестиугольника, поворот на 180° луча, соединяющего вершину с центром, и совместить его с отражением. Исходя из этих движений, можно, например, составить симметричную раскраску фрагментов. На рис. 17б - самый общий шаблон для возможных вариантов симметричной раскраски шестиугольной мозаики. Раскрасьте шестиугольную мозаику в 3 цвета, используйте для этого линии отражения и хорошо видные на чертеже центры поворота на 60° (центр шестиугольника), на 120° (центр треугольника), на 180° (вершины вписанного шестиугольника). Вписанные шестиугольники порождают покрытие, состоящие из 2-х правильных многоугольников – шестиугольника и равностороннего треугольника (рис. 17в).
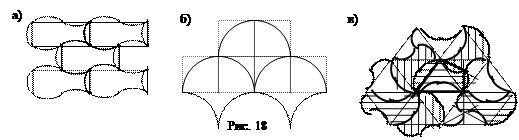
Прямые линии в кванте можно заменить на кривые. При этом надо следить, чтобы кривой кусок границы переходил в симметричный ему кусок с помощью разрешенного для данной решетки движения. На рисунках 18а,б приведены совсем простые примеры искривления ребер для прямоугольной решетки с помощью дуг окружности. На рисунке 18в в шестиугольнике выделено 6 одинаковых квантов, искривление ребер этих квантов производится также с помощью дуги окружности, для которой ребро является хордой. Длинные стороны четырехугольника переходят друг в друга с помощью поворота на 60°, короткие – с помощью поворота на 120°. Вокруг точки пересечения короткого и длинного ребра поворот на 180°. Полученные лепестки раскрашены в 3 цвета.
Замечательные мозаики, кванты для которых имеют вид рыб, птиц и животных созданы голландским художником-графиком Эшером. По тому же принципу, по которому мы построили мозаику из цветка, состоящего из 6-ти лепестков 3-х разных цветов, он построил мозаику из "цветков", у которых в качестве "лепестка" взята ящерица.
Орнамент Ящерицы. М. Эшер.
В качестве ячейки сетки, по которой строится мозаика, могут выступать фигуры не обязательно "правильной" формы. Попробуйте построить мозаику из треугольников и четырехугольников (например, трапеций) произвольного вида.
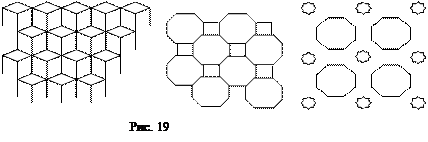
Разумеется, можно строить сплошной симметричный узор не только из одной, а и из нескольких фигур. Художественные паркеты строятся, как правило, из 2-х и более элементов. На рисунке 19 приведены примеры самых простых паркетов из петербургских дворцов. Эшер создал великолепные примеры "упорядоченного членения плоскости" с помощью 2-х фигур (всадник и лошадь, птица и рыба) и даже с помощью восьми фигур. Детальные схемы и примеры к ним для симметричных розеток, бордюров, мозаик и плетений можно найти, например, в книге Гинзбурга «Симметрия на плоскости».
Задачи для самостоятельного решения. 1. Построить равносторонний треугольник и его центр. 2. Построить сетку из треугольников. 3. Начертить циркулем и линейкой свастику, пятиконечную звезду, звезду Давида, правильный восьмиугольник и звездчатый восьмиугольник. 4. Начертить круговую диаграмму, в которой есть сектора, составляющие 10%, 20%, 25%, 33,3% площади. 5. Магазин получил 3000 компьютеров. В течение года почти все оказались распроданы. Из них 300 штук купили частные пользователи, 600 штук купили школы, 1000 штук - научные институты, 750 - предприятия. Нарисовать круговую диаграмму продаж. 6. Создать розетку из 6 или 8 секторов. Начертить объемлющий круг, его поделить на вдвое большее число секторов (12 или 16, соответственно). Вписать в сектора какие-нибудь узоры, используя симметричное отражение и повороты. 7. Начертить ленточный бордюр, используя отражения по вертикали, по горизонтали и перенос. 8. Начертить эскиз решетки на основе дуг плотно уложенных кругов. 9. Начертить эскиз решетки на основе дуг полуокружностей. 10. Начертить эскиз произвольной решетки из крестов. 11. Начертить эскиз решетки из таких крестов, что фон между крестами имеет форму такого же креста. 12. На рисунке 21 приведены фрагменты решеток. Исправьте ребро так, чтобы форма кванта фона совпала с формой кванта основного рисунка.
13. Сделать эскиз паркета с квадратной, прямоугольной, параллелограммной, треугольной и ромбической плиткой. 14. Построить сетку из треугольников в основания которых а)горизонтальны, б)вертикальны, выделить пчелиные соты, провести все прямые симметрии. 15. Поделить шестиугольники пчелиных сот на 6 лепестков. Раскрасить лепестки в 3 цвета. 16. Начертить свободный эскиз мозаики без искривления сторон (для решетки, для пола, для обоев, с использованием цвета или без). 17. Начертить свободный эскиз мозаики с искривлением сторон.
Глава 4 Пропорции
Понятие пропорции Пропорцией называется равенство двух отношений: 190 х =20×114 х= 20×114:190=12 Параллельные прямые, пересекающие угол, отсекают на сторонах угла пропорциональные отрезки (рис. 1а). Это позволяет построить геометрическое решение задачи о нахождении неизвестного члена пропорции (рис. 1б). Применение пропорций помогает решать задачи, в которых участвуют подобные треугольники (рис. 1в).
Например, во сколько раз увеличится основание треугольника, если сделать его подобное преобразование, увеличив высоту в l раз? Согласно теореме о пересечении угла параллельными прямыми, оно увеличится тоже в l раз. Следовательно, площадь треугольника при увеличении высоты в l раз увеличится в l2 раз. Например, при увеличении высоты вдвое площадь треугольника увеличивается в 4 раза. На рис. 1 больший треугольник состоит из 4-х одинаковых треугольников.
Преобразование подобия. Гомотетия Преобразование фигуры F в фигуру F1 называется преобразованием подобия, если при этом преобразовании расстояния между точками фигуры изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Это значит, что если произвольные точки M и N фигуры F при этом преобразовании переходят в точки M1 и N1 фигуры F1, то M1N1=k×MN; число k называется коэффициентом подобия. При k=1 преобразование подобия, очевидно, является движением. Преобразование подобия переводит прямые в прямые, полупрямые в полупрямые и отрезки в отрезки и сохраняет углы между полупрямыми. Две фигуры называются подобными, если они переходят друг в друга преобразованием подобия. У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. Таким образом, подобные фигуры имеют одинаковую форму и пропорциональные размеры. Проще всего построить подобное изображение фигуры с помощью так называемой гомотетии. Гомотетией с центром О и коэффициентом k>0 называется такое преобразование, при котором произвольная точка М любого луча, исходящего из точки О, переходит в точку М1 того же луча, причем ОМ1=k×ОМ. Пусть F – данная фигура, О – некоторая точка, k – заданное положительное число. Возьмем произвольную точку М фигуры F. Проведем луч ОМ и отложим на нем отрезок ОМ1, равный k×ОМ. Получим точку М1 новой фигуры F1. Преобразование фигуры F в фигуру F1 есть гомотетия с центром О и коэффициентом k (рис. 2). Фигуры F и F1 называются гомотетичными. Если фигура F1 получена из фигуры F с помощью гомотетии с коэффициентом k, то все ее линейные размеры в k раз больше при k>1, или в k раз меньше при k<1, и все углы у обеих фигур одинаковые. Площадь S1 фигуры F1 будет больше при k>1 (или меньше при k<1) площади S фигуры F в k2 раз. Гомотетию можно использовать для изменения масштаба в k раз. Центр гомотетии может лежать, как внутри фигуры, так и вне нее (рис. 2).
Гомотетия есть частный случай преобразования подобия. Если мы фигуру F преобразуем в фигуру F1 с помощью гомотетии с некоторым центром О и коэффициентом k, а затем "передвинем" (перенесем, повернем, отразим), то фигуры F и F1 будут подобны, но не гомотетичны.
Пропорция
Прямоугольник, отношение длин сторон которого Пропорция «квадрата и его диагонали» использовались русскими мастерами еще в самые древние времена. (о методе «квадрата и диагонали» см. ниже). Для многих практических целей вместо построения с помощью циркуля и линейки желательно иметь приближение числа
приближение для
Действительно, если обозначить эту дробь через х, то дробь под первой чертой будет равна 1 +х. Тем самым:
Обрывая дробь перед первым, вторым, третьим и т.д. знаком плюс, мы будем получать улучшающиеся с каждым шагом приближенные значения числа Гипернормальным называется такой прямоугольник, что если от него отрезать два квадрата, то получится новый гипернормальный прямоугольник. Его можно построить из двух одинаковых нормальных прямоугольников (на рис. 3в заштрихованный прямоугольник гипернормальный). Если обозначить длину большей стороны прямоугольника через a+b, а меньшей стороны через b, то для гипернормального прямоугольника выполняется:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.011 с.) |


 Если фигура F с помощью движения переводится в фигуру F1, то говорят, что они равны. Таким образом, мозаика имеет дело с равными фигурами, заполняющими плоскость без наложения друг на друга. У фигур, построенных на основе принципов симметрии, даже с искривленными границами, легко вычисляется площадь. У искривленного квадрата площадь равна площади самого квадрата (фигуру, которую вырезали с одной стороны, приклеили к нему с другой стороны). При построении рыбки мы пользовались именно этим принципом. Лепесток цветка в шестиугольной мозаике можно разрезать на 2 части. Ушестеренная первая часть заполняет без наложений шестиугольник, утроенная вторая часть – треугольник. Следовательно, площадь лепестка составляет 1+1/3=4/3 площади треугольника (шестиугольник состоит из 6 таких треугольников). Правило сохранения величины площади после искривления границы кванта можно использовать для проверки – не нарушили ли вы при искривлении правила возможных движений решетки.
Если фигура F с помощью движения переводится в фигуру F1, то говорят, что они равны. Таким образом, мозаика имеет дело с равными фигурами, заполняющими плоскость без наложения друг на друга. У фигур, построенных на основе принципов симметрии, даже с искривленными границами, легко вычисляется площадь. У искривленного квадрата площадь равна площади самого квадрата (фигуру, которую вырезали с одной стороны, приклеили к нему с другой стороны). При построении рыбки мы пользовались именно этим принципом. Лепесток цветка в шестиугольной мозаике можно разрезать на 2 части. Ушестеренная первая часть заполняет без наложений шестиугольник, утроенная вторая часть – треугольник. Следовательно, площадь лепестка составляет 1+1/3=4/3 площади треугольника (шестиугольник состоит из 6 таких треугольников). Правило сохранения величины площади после искривления границы кванта можно использовать для проверки – не нарушили ли вы при искривлении правила возможных движений решетки.
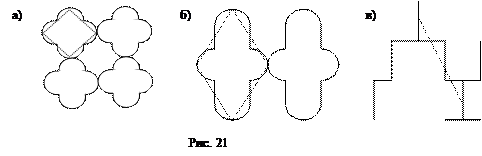
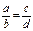 . Это равенство можно переписать в виде: ad= b, что позволяет найти любой член пропорции, если известны три других ее члена. Например, найти неизвестный член пропорции х, если
. Это равенство можно переписать в виде: ad= b, что позволяет найти любой член пропорции, если известны три других ее члена. Например, найти неизвестный член пропорции х, если 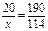 . Решение такое.
. Решение такое.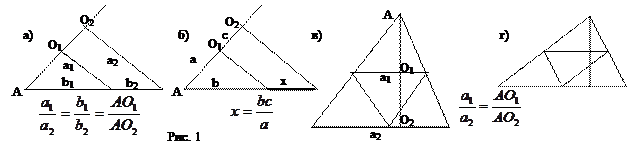

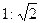 . Нормальный полиграфический лист
. Нормальный полиграфический лист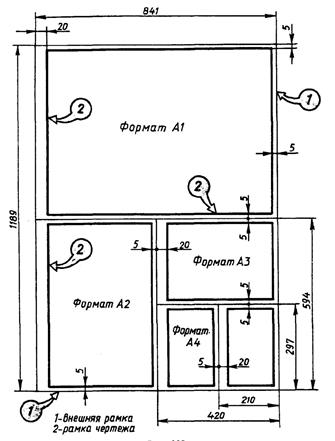 Будем говорить, что лист бумаги нормальный, если при сложении его вдвое получится подобный ему лист (рис. 3а). Если а и b означают длинную и короткую стороны нормального листа, то: a:b=b:a/2. Отсюда следует, что a2=2b2 и
Будем говорить, что лист бумаги нормальный, если при сложении его вдвое получится подобный ему лист (рис. 3а). Если а и b означают длинную и короткую стороны нормального листа, то: a:b=b:a/2. Отсюда следует, что a2=2b2 и 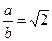 . Такая форма листа положена в основу типографских стандартов: А0:1189´841мм2, А1:841´594мм2, А2:594´420мм2, А3:420´297мм2, А4:297´210мм2. Площадь А0 – 1м2, площадь А1 – 0.5м2 и т.д. (рис.3а). Такие пропорции имеют газетные листы, листы ватмана, листы бумаги для компьютера. Эта форма позволяет разрезать без обрезков бумагу на куски стандартной пропорции
. Такая форма листа положена в основу типографских стандартов: А0:1189´841мм2, А1:841´594мм2, А2:594´420мм2, А3:420´297мм2, А4:297´210мм2. Площадь А0 – 1м2, площадь А1 – 0.5м2 и т.д. (рис.3а). Такие пропорции имеют газетные листы, листы ватмана, листы бумаги для компьютера. Эта форма позволяет разрезать без обрезков бумагу на куски стандартной пропорции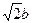 (рис. 3б). Прямоугольник такой формы называется нормальным.
(рис. 3б). Прямоугольник такой формы называется нормальным. в виде отношения p/q двух целых чисел p и q. Это позволило бы чертить прямоугольник нормальной пропорции на "клетчатой" бумаге. При этом хотелось бы, чтобы q имело минимальное значение. Число
в виде отношения p/q двух целых чисел p и q. Это позволило бы чертить прямоугольник нормальной пропорции на "клетчатой" бумаге. При этом хотелось бы, чтобы q имело минимальное значение. Число 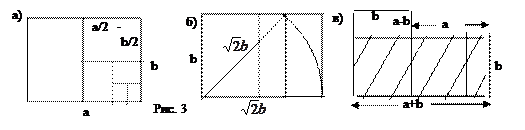
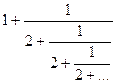 .
.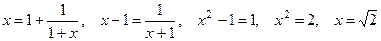 .
.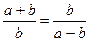 . Желающие могут проделать выкладки самостоятельно и получить, что отношение сторон у гипернормального прямоугольника:
. Желающие могут проделать выкладки самостоятельно и получить, что отношение сторон у гипернормального прямоугольника: 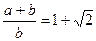 »2,414.
»2,414.


