
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение сложной и простой схемыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таким образом, наращенная сумма Sn за n лет по схеме простых процентов Sn=S(1+ni), по схеме сложных процентов Sn=S(1+i)n. На рисунке 1 графически изображено изменение во времени наращенной суммы по обеим схемам.
Задачи для самостоятельного решения 1. х=2,3752±1%. В каких пределах находится значение? Сколько верных знаков? 2. Предполагается, что в древнем Египте для вычисления площади круга использовалась формула 3. Продан товар на 1386 рублей. Получена прибыль 10%. Какова себестоимость товара S? 4. Цену товара снизили на 20%, затем на 15%, затем еще на 10%. На сколько процентов снизили первоначальную цену? 5. Вес задан с точностью 5%. Это пишут так: S(±5%). Если вес S=124, то в каких границах находится истинный вес? 6. На сколько процентов увеличится площадь квадрата, если сторону его увеличить на 20%? 7. Число q задано с точностью 1%. Какова точность значения qn для n=2,3,4,5? 8. Банк платит по рублевому вкладу 18% годовых, а по валютному –8%. Цена доллара за год выросла с 25рублей за доллар до 27руб. 50 коп. за доллар. Какой вклад оказался выгоднее? 9. За 8 лет капитал увеличился в 1,5 раза. Какой ставке наращения это соответствует? Указание. Извлечение корня 4-ой, 8-ой, 16-ой, любой 2к-ой степени можно выполнить с помощью калькулятора: чтобы извлечь корень 4-ой степени, надо нажать на кнопку извлечения корня два раза подряд, 8-ой степени - 3 раза подряд, 16-ой - 4 раза подряд и так далее; это следует из формулы 10. Представьте себе, что при рождении Христа на его имя была положена в банк под 1% годовых 1 копейка. Оцените - каков размер этого вклада в настоящее время? Каким будет размер вклада, если копейка была положена под 6% годовых?
Глава 2 Арифметическая и геометрическая прогрессии
Метод полной индукции В основе всякого научного исследования, в том числе и математического, лежат дедуктивный и индуктивный метод. Дедукция – переход от общего к частному. Примером рассуждения такого типа в математике является, например, такое рассуждение: данная фигура прямоугольник; у каждого прямоугольника диагонали равны, следовательно, и у данного прямоугольника диагонали равны. Индукция – вид обобщений, связанных с предвосхищением результатов наблюдений и экспериментов на основе уже имеющихся данных. Индуктивный подход обычно начинается с анализа данных наблюдения или эксперимента. Многократность повторения какого-либо факта приводит к индуктивному обобщению. Конечно, для практики характерны обобщения на основе исследования не всех случаев, а только некоторых. Такие обобщения называются неполной индукцией. Неполная индукция может привести к ошибочным результатам. Если же общее утверждение удается доказать во всех возможных случаях, то такая индукция называется полной. Провести проверку утверждения для бесконечного числа случаев позволяет метод рассуждений, называемый методом математической индукции. Метод состоит в том, что для того, чтобы доказать, что утверждение, зависящее от натурального числа n, справедливо для любого n,надо проверить выполнение 2-х условий: а) утверждение справедливо при n=1; б) из справедливости утверждения для конкретного значения n=k вытекает его справедливость и для следующего за ним значения n=k+1. Смысл рассуждения очень простой. Сначала убеждаемся, что утверждение верно для n=1. Если удается показать, что из справедливости утверждения для конкретного значения n=k вытекает его справедливость и для следующего за ним значения n=k+1, то из того, что утверждение верно для n=1, получается, что оно верно и для следующего натурального значения n=2, из этого следует, что оно верно и для следующего натурального значения n=3 и т.д. Тем самым, оно верно для любого n.
Пример Доказать, что при любых натуральных n справедливо: Sn=1+3+5+7+…+(2n-1)=n2 Доказательство: а)S1=1=12, следовательно, утверждение верно для n=1. б)Пусть утверждение верно для натурального числа, n=k, то есть: Sk=1+3+5+…+(2k-1)=k2 Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, то есть докажем, что: Sk+1=1+3+5+…+(2k-1)+(2k+1)=(k+1)2 Для этого воспользуемся тем, что для значения k верно: Sk=1+3+5+…+(2k-1)=k2. Sk+1=1+3+5+…+(2k-1)+(2k+1)=Sk+(2k+1)=k2+2k+1=(k+1)2 Тем самым, формула верна для всех натуральных n.
Арифметические прогрессии Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью прогрессии. Члены арифметической прогрессии мы будем обозначать через а1,а2,…,аn,…, разность прогрессии – через d. Таким образом: а1, а2=а1+d, a3=a2+d=a1+d+d=a1+2d, a4=a3+d=a1+2d+d=a1+3d, ……….
Примеры 1. Последовательность чисел 1, 2, 3, 4,…(эта последовательность называется натуральным рядом) – арифметическая прогрессия с разностью d=1 и начальным членом а1=1. 2. Последовательность чисел 0, -1, -2, -3, -4,… – арифметическая прогрессия с разностью d=-1 и начальным членом а1=0 3. Последовательность чисел 10, 8, 6, 4, 2, 0, -2, -4,… – арифметическая прогрессия с разностью d=-2 и начальным членом а1=10.
Покажем, что член арифметической прогрессии с номером n можно вычислить по формуле: аn=а1+d(n-1) Докажем эту формулу методом математической индукции. а) а1=а1+0=а1, следовательно, для n=1 формула верна; б) пусть для натурального значения k выполняется: ak=a1+(k-1)d. Покажем, что из этого следует, что формула верна и для следующего натурального числа k+1. Воспользуемся тем, что: ak+1=ak+d по определению арифметической прогрессии и ak=a1+(k-1)d согласно б). Следовательно, ak+1=ak+d=а1+(k-1)d+d=a1+kd и формула верна для всех натуральных n. Тем самым, для того, чтобы задать арифметическую прогрессию, достаточно задать значения ее первого члена а1 и ее разности d.
Примеры решения задач 1.Свободно падающее тело проходит за первую секунду 4,9 м, а в каждую следующую секунду на 9,8м больше, чем в предыдущую. Какое расстояние будет пройдено за 5-ую секунду? Решение: Пути, проходимые за 1-ю, 2-ю, 3-ю и т.д. секунды образуют арифметическую прогрессию, у которой а1=4,9, d=9,8. Следовательно, а5=4,9м+4×9,8м=44,1м. 2. Курс воздушных ванн врачи рекомендуют начинать с 15 мин. в первый день, а затем увеличивать время этой процедуры каждый следующий день на 10 мин. Через сколько дней будет достигнута нужная продолжительность в 1час 45мин.? Решение: Последовательность значений длительности процедуры в первый, второй и т.д. день представляет собой арифметическую прогрессию с первым членом а1=15мин. и разностью d=10мин. Таким образом, надо найти номер n члена прогрессии, для которого an=1час45мин=105мин, т.е. надо найти n из уравнения: an=a1+d(n-1)=105. Подставив в формулу а1=15 и d=10 и решив уравнение, получим: 15+10(n-1)=105, или n=10 дней
Сумма n первых членов арифметической прогрессии вычисляется по формуле:
Доказательство того, что эта формула верна при всех n, проведем методом математической индукции. а)S1=a1, следовательно, для n=1 формула верна; б)Покажем, что если формула верна для значения k, то она верна и для следующего натурального числа k+1. Имеем:
Примеры решения задач 1.Сумма первых n членов натурального ряда: 1+2+3+…+n= 2.Сумма первых n членов ряда нечетных чисел: 1+3+…+(2n-1)=n2, так как последовательность нечетных чисел - арифметическая прогрессия, у которой а1=1, d=2. 3.Рабочему поручили вырыть колодец и условились платить ему за первый метр глубины 100 руб., за второй – 300 руб. и т.д., увеличивая плату за каждый следующий метр на 200 рублей. Сколько надо заплатить рабочему, если он вырыл колодец на глубину 10 м? Решение: Числа 100, 300, 500… (плата за 1-ый, 2-й, 3-й метр глубины) образуют арифметическую прогрессию, у которой а1=100, d=200. Плата за весь колодец – сумма ее первых 10 членов. Подставляем в формулу наши данные: S10=0,5(2×100+9×200)×10=10000 4.При хранении бревен их уложили так: положили на землю 12 бревен, на них сверху в пазы нижнего ряда 11 бревен и т.д. до тех пор, пока пирамида не закончится одним бревном (см. рисунок 1). Сколько бревен в такой кладке? Сколько бревен в кладке, начинающейся с 8 бревен?
Числа 12,11, 10,,1 - количество бревен на 1-м,2-м,3-м,…,12-м уровне, образуют арифметическую прогрессию, для которой а1=12, a12=1. Для того, чтобы найти сумму S12, воспользуемся формулой: Sn=(аn+a1)n/2 S12=6×(12+1)=78; Аналогично, если кладка начинается с 8 бревен, то n=8, S8=4×(8+1)=36.
Геометрическая прогрессия Геометрической прогрессией называется последовательность не равных нулю чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число. Это постоянное число называется знаменателем прогрессии. Члены геометрической прогрессии будем обозначать через b1, b2, b3,…,bn,…, знаменатель прогрессии - через q. Таким образом: b1, b2=b1×q; b3=b2×q=b1×q2 b4=b3×q=b1×q3 …..
Примеры 1. Последовательность чисел 1; 0,1; 0,01; 0,001;… суть геометрическая прогрессия со знаменателем q=0,1 и b1=1. 2. Последовательность чисел 1, 10, 100, 1000,… суть геометрическая прогрессия со знаменателем q=10 и b1=1. 3. Последовательность чисел 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 –геометрическая прогрессия со знаменателем q=2 и b1=2 (по-другому эту последовательность можно записать так: 2, 22, 23, 24, 25, 26, 27, 28, 29, 210).
Покажем, что член геометрической прогрессии с номером n можно вычислить по формуле: bn=b1×qn-1 Эту формулу докажем также методом математической индукции. а) b1=b1q0=b1, следовательно, для n=1 формула верна; б) Пусть для значения k выполняется: bk=b1×qk-1. Покажем, что формула будет верна и для следующего натурального числа k+1. Воспользуемся тем, что: bk+1=bk ×q по определению геометрической прогрессии и bk=b1×qk-1 согласно б). Следовательно, bk+1=bk×q=b1×qk-1×q=b1×qk и формула верна для всех натуральных n. Тем самым, для того, чтобы задать геометрическую прогрессию достаточно задать ее первый член b1 и ее знаменатель q. Геометрическая прогрессия, у которой |q|<1 (каждый следующий член по модулю меньше предыдущего), называется убывающей, а если |q|>1, то она называется возрастающей (каждый следующий член по модулю больше предыдущего). Например, последовательность 2, 22, 23, 24,…, 2n,… - возрастающая геометрическая прогрессия, у которой b1=2, q=2; последовательность 1, 0,1; 0,01; 0,001;…, (10)-n,… - убывающая геометрическая прогрессия, у которой b1=1, q=0,1.
Примеры решения задач 1.Каждое простейшее одноклеточное животное инфузория-туфелька размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 320? Решение: Обозначим через x первоначальное количествоинфузорий. После 1-ого деления их стало 2 х, после второго 2×2× x, после третьего 2×2×2× x, и т.д., после шестого 26 х =64 х =320. Отсюда х =5, т. е. с самого начала было 5 инфузорий. 2. Частота колебаний каждой конкретной ноты (до, до диез, ре, ми бемоль, ми и т.д. – всего 12 нот) при переходе к следующей октаве увеличивается вдвое. Октава делится на 12 равных интервалов-полутонов. Частота каждого последующего звука больше частоты предыдущего в Решение: Нота ми выше ноты до той же октавы на 4 полутона (2 черные клавиши и 2 белые). Следовательно, ее частота выше частоты ноты до в
Сумма n первых членов геометрической прогрессии вычисляется по формуле:
(формула также легко доказывается методом математической индукции, желающие могут в качестве упражнения провести доказательство самостоятельно).
Пример Согласно древней легенде индийский царь Шерам был восхищен новой игрой – шахматами и предложил ее изобретателю мудрецу Сете любую награду. Сете попросил плату пшеницей, исходя из следующего расчета: за первую клетку заплатить одно зерно, за вторую – 2 зерна, за третью 4 зерна и т.д. – за каждую следующую клетку дать в 2 раза больше зерен, чем за предыдущую. Сколько зерен попросил Сете? Решение: Последовательность чисел – число зерен на клетке, является геометрической прогрессией, для которой b1=1, q=2. Надо найти Sn для n=64. Подставляем в формулу. S64=(264-1):(2-1)=264-1. Для того, чтобы оценить эту величину, вспомним, что 210=1024»103, 24=16, следовательно, 264-1»(103)6×16=1019×1,6. Для вычисления точного значения этого числа нельзя воспользоваться калькулятором, так как это число содержит 20 цифр, а калькулятор содержит только 8 первых точных цифр. Можно вычислить, что если бы такое число зерен рассыпать равномерно по всей земной суше, то образовался бы слой пшеницы толщиной около 9 мм.
Рассмотрим последовательность, члены которой суть разность соседних членов геометрической прогрессии: c1 =b1-b2=b1(1-q) c2 =b2-b3=b2(1-q)=b1q(1-q)=b1(1-q)q=c1q c3 =b3-b4=b3(1-q)=b1q2(1-q)=b1(1-q)q2=c2q=c1q2 ……… сn=bn-bn+1 =cn-1q=c1qn-1 (легко доказать методом полной индукции) Разность соседних членов геометрической прогрессии, таким образом, есть также геометрическая прогрессия, первый член которой равен разности 2-х первых членов первой прогрессии b1(1-q), а знаменатель совпадает со знаменателем первой прогрессии, то есть равен q. Сумма Sn первых n членов такой прогрессии равна:
Заметим, что разность членов арифметической прогрессии есть величина постоянная, равная разности арифметической прогрессии d (вырожденная прогрессия).
Бесконечные прогрессии Сумма всех членов бесконечной убывающей геометрической прогрессии вычисляется по формуле:
(так как при q<1 Легко видеть, что для бесконечной прогрессии сi, члены которой суть разность членов геометрической прогрессии имеем:
Пример 1. Найти сумму бесконечной геометрической прогрессии, у которой b1=1, q=1/2. Выпишем несколько первых членов этой прогрессии и формулу ее n-ого члена:
Согласно формуле
Геометрическая прогрессия ci, членами которой являются разности членов этой прогрессии: Нарисуем окружность радиуса r1=R и центром О. Зададим некоторый коэффициент q<1 и нарисуем вокруг того же центра О окружности радиуса r2=Rq, r3=Rq2, r4=Rq3,…, rn=Rqn-1 . Значения радиусов образуют геометрическую прогрессию со знаменателем q и b1=R. С ростом номера окружности радиусы окружностей становятся все меньше.
На рисунке 2а изображены 4 окружности, построенные по этому алгоритму для q=1/2. Ширина колец между окружностями – также геометрическая прогрессия с тем же знаменателем q=1/2. А формула
На рисунке 2г изображены первые 4 окружности, построенные по этому алгоритму, для q=1/2. Приведенная формула показывает, что для q=1/2 суммарная площадь всех колец S=2R. На рисунке 2д приведено то же построение для квадратов. Для длины стороны квадрата верны те же формулы, что и для радиуса окружности. Следовательно при q=1/2 вся конструкция впишется в квадрат, сторона которого вдвое больше стороны первоначального квадрата. Для сравнения на рисунках 2е и 2ж изображены 4 окружности и 4 квадрата, размеры радиусов и сторон которых определяются арифметической прогрессией.
Рис. 3: Пределы и самоподобие в гравюрах М. Эшера
Примеры из финансовых расчетов Все приведенные здесь формулы находят широкое применение в самых разных областях. Например, в сфере банковских расчетов, когда в финансово-банковских операциях участвуют не разовые платежи, а некоторая последовательность платежей во времени. Рассмотрим самый простой случай. Пусть в течение n лет в банк в конце каждого года вносится R рублей. На взносы начисляются сложные проценты по ставке i% годовых (i= R(1+i)n-1, R(1+i)n-2,…, R(1+i), R. Перепишем этот ряд в обратном порядке. Легко видеть, что он представляет собой геометрическую прогрессию со знаменателем (1+i) и первым членом R. Число членов прогрессии равно n. Следовательно, наращенная сумма такого потока вычисляется по формуле:
При n=1 наращенная сумма S1=R. При i=0 (нет наращения) формула не работает, но она и не нужна, так как Sn=nR. При i>0 наращенная сумма Sn>nR.
Задачи 1. Для обеспечения некоторых будущих расходов создается фонд. Средства в фонд поступают в течение 4 лет в виде взносов 4млн. рублей в конце года. На поступившие взносы начисляются проценты по ставке 12% годовых. Величина фонда на конец срока составит:
Заметим, что внесено в фонд в виде взносов было 16 млн. руб. (чт о соответствует i=0). 2. Через 3 года понадобится для организации начала работ 1млн. руб. Какими должны быть ежегодные взносы в банк, начисляющий 10% годовой прибыли? Решение: Взносы будем производить по схеме: сразу кладем в банк R рублей, через год, еще R рублей, через 2, через 3 года по R рублей. Всего 4 взноса. Через 3 года наращенные платежи станут такими: R(1+0,1)3, R(1+0,1)2, R(1+0,1), R. Выписав члены последовательности в обратном порядке, получим геометрическую прогрессию с начальным членом b1=R, знаменателем q=1+0,1=1.1, n=4. Значение суммы нам известно, это 1 млн. руб. - столько мы должны накопить к концу срока. По формуле суммы геометрической прогрессии имеем:
Подставляем в формулу наши данные: 1000000=R×(1,14-1):0,1=R×10×(1,4641-1)=R×4,641; R=1000000:4,641=215.470,8руб. Задачи для самостоятельного решения 1. Сколько членов надо взять в арифметической прогрессии: 4, 8,…, чтобы их сумма равнялась 112? 2. Выписать первые 11 членов геометрической прогрессии, у которой b1=1 и а)q=2, b)q=1/2. Для этих прогрессий выписать первые 10 членов последовательностей, члены которых есть разность двух соседних членов геометрической прогрессии. 3. Выписать первые 9 членов геометрических прогрессий, если: а) b1=1/16, q=2, b) b1=16, q=1/2. 4. Нарисовать 5 концентрических окружностей, радиусы которых образуют геометрическую прогрессию со знаменателем: а) q=1/2, б) q=2 5. Выписать 5 первых членов геометрической прогрессии, если b1=1, а) q=0,6; б) q=0,618. Для этих прогрессий выписать первые 5 членов последовательностей, члены которых есть разность двух соседних членов геометрической прогрессии. Если рассматривать 0,6 как приближение для 0,618, то какова будет точность приближения для 2-ого, 3-его, 4-ого и 5-ого члена прогрессии? Указание. Воспользоваться формулами:q=q1-D, qn=(q1-D)n=q1n 6. Выписать 5 первых членов геометрической прогрессии, если b1=1, а) q1=1,6; б) q2=1,618. Для этих прогрессий выписать первые 5 членов последовательностей, члены которых есть сумма двух стоящих рядом членов геометрической прогрессии: u1+u2, u2+u3,…. 7. Нарисовать 5 концентрических окружностей, радиусы которых образуют геометрическую прогрессию со знаменателем а) q=0,6, б) q=1,6
Глава 3
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.014 с.) |

 График показывает, что для срока, величина которого меньше года, при равных сроках начисления процентов и одинаковых ставках наращения i простые проценты дают наращение больше сложных, для срока, равного году, наращения совпадают, в дальнейшем с каждым новым периодом наращения разница между простыми и сложными процентами увеличивается – по сложной схеме проценты растут гораздо быстрее, так как степенная функция (1+i)n растет гораздо быстрее, чем линейная 1+ni.
График показывает, что для срока, величина которого меньше года, при равных сроках начисления процентов и одинаковых ставках наращения i простые проценты дают наращение больше сложных, для срока, равного году, наращения совпадают, в дальнейшем с каждым новым периодом наращения разница между простыми и сложными процентами увеличивается – по сложной схеме проценты растут гораздо быстрее, так как степенная функция (1+i)n растет гораздо быстрее, чем линейная 1+ni. . Какова точность (в процентах) получающейся из этой формулы оценки для числа p?
. Какова точность (в процентах) получающейся из этой формулы оценки для числа p? ). Проверьте. Трехкратное извлечение корня из числа 2 дает: 1+i=1,090508. Таким образом, чтобы решить задачу, надо набрать на калькуляторе 1,5 и 3 раза нажать на кнопку
). Проверьте. Трехкратное извлечение корня из числа 2 дает: 1+i=1,090508. Таким образом, чтобы решить задачу, надо набрать на калькуляторе 1,5 и 3 раза нажать на кнопку  , по получившемуся значению установить ставку наращения.
, по получившемуся значению установить ставку наращения.
 . Следовательно, формула верна для всех n.
. Следовательно, формула верна для всех n. (натуральный ряд – арифметическая прогрессия у которой а1=1, d=1).
(натуральный ряд – арифметическая прогрессия у которой а1=1, d=1). Решение:
Решение: »1,0595 раз (корень степени 12 из числа 2 можно извлечь с помощью таблиц или инженерного калькулятора). Во сколько раз нота ми выше ноты до той же октавы?
»1,0595 раз (корень степени 12 из числа 2 можно извлечь с помощью таблиц или инженерного калькулятора). Во сколько раз нота ми выше ноты до той же октавы? ≈1,05954»1,26 раз.
≈1,05954»1,26 раз.


 )
)

 имеем:
имеем: 
 Ее сумма S=1.
Ее сумма S=1.
 получает геометрический смысл – кольца в совокупности покроют всю окружность. На рисунке 2б то же построение выполнено для квадратов. На рисунке 2в приведено построение последовательности отрезков, длины которых образуют геометрическую прогрессию: a, aq, aq2, aq3, aq4. Мы воспользовались тем, что прямоугольники, у которых длины сторон равны величине двух соседних членов прогрессии, подобны (отношение длин их сторон равно q), следовательно, их вершины лежат на одной прямой, проходящей через их диагональ. Теперь рассмотрим случай, когда ширина концентрических колец образует прогрессию с b1=R и q<1. Сначала рисуем окружность радиуса R, затем отмечаем ширину кольца, равную Rq, полученным радиусом (он равен R+Rq) проводим вторую окружность, отмечаем ширину кольца Rq2, полученным радиусом (R+Rq+Rq2) проводим третью окружность и т.д. С помощью этого алгоритма можно построить бесконечное количество концентрических окружностей. Все они впишутся в окружность, радиус которой вычисляется, как сумма бесконечной геометрической прогрессии:
получает геометрический смысл – кольца в совокупности покроют всю окружность. На рисунке 2б то же построение выполнено для квадратов. На рисунке 2в приведено построение последовательности отрезков, длины которых образуют геометрическую прогрессию: a, aq, aq2, aq3, aq4. Мы воспользовались тем, что прямоугольники, у которых длины сторон равны величине двух соседних членов прогрессии, подобны (отношение длин их сторон равно q), следовательно, их вершины лежат на одной прямой, проходящей через их диагональ. Теперь рассмотрим случай, когда ширина концентрических колец образует прогрессию с b1=R и q<1. Сначала рисуем окружность радиуса R, затем отмечаем ширину кольца, равную Rq, полученным радиусом (он равен R+Rq) проводим вторую окружность, отмечаем ширину кольца Rq2, полученным радиусом (R+Rq+Rq2) проводим третью окружность и т.д. С помощью этого алгоритма можно построить бесконечное количество концентрических окружностей. Все они впишутся в окружность, радиус которой вычисляется, как сумма бесконечной геометрической прогрессии:




 Рис. 3а: Пределы и самоподобие в гравюрах М. Эшера
Рис. 3а: Пределы и самоподобие в гравюрах М. Эшера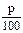 – p – процент наращения, i – ставка наращения). Все взносы, кроме последнего, приносят проценты – на первый взнос проценты начисляются n-1 раз, на второй – n-2 раза и т.д. На последний взнос проценты не начисляются. Наращенные к концу срока суммы составят:
– p – процент наращения, i – ставка наращения). Все взносы, кроме последнего, приносят проценты – на первый взнос проценты начисляются n-1 раз, на второй – n-2 раза и т.д. На последний взнос проценты не начисляются. Наращенные к концу срока суммы составят:

 . (сравнить q1 и q2, q12 и q22 и т.д.).
. (сравнить q1 и q2, q12 и q22 и т.д.).


