
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наращение и дисконтирование с использованием схемы сложных процентовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если инвестиция сделана на условиях сложного процента, то очередной годовой доход исчисляется не с исходной величины инвестируемого капитала, а с общей суммы, которая включает также ранее начисленные, но не востребованные инвестором проценты. В этом случае имеет место капитализация процентов по мере их начисления, так как база, с которой начисляются проценты, все время возрастает. Таким образом, на протяжении срока финансовой операции размер инвестированного капитала будет равен: к концу первого года: к концу второго года: и так далее … к концу n-го года: Это равенство называется формулой наращения по сложным процентам; множитель Согласно формулы сложных процентов приращение капитала составит:
Формула наращения по сложным процентам является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования составлены специальные таблицы для определения
где
Экономический смысл множителя Рассмотренная формула предполагает, что Как и в случае начисления простых процентов, финансовое соглашение может предусматривать плавающие процентные ставки и при наращении по сложным процентам. Пусть
Обозначим Таким образом, в течение всего периода финансовой операции можно установить сложную ставку Пример. Предприниматель получил в банке ссуду в размере 40 тыс. грн. сроком на 7 лет на следующих условиях: для первого года процентная ставка равна 15% годовых, на следующие два года устанавливается маржа в размере 0,8% и на следующие годы маржа равна 0,9%. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды.
Такая же величина наращенной суммы получится, если в течение 6 лет проценты будут начисляться по средней процентной ставке за весь период финансовой операции.
Достаточно часто заключаются финансовые контракты, продолжительность которых отличается от целого числа лет. В этом случае проценты могут начисляться с помощью следующих двух методов:
Ø по схеме сложных процентов:
Ø по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов для дробной части года):
где w - целое число лет; f - дробная часть года. Пример. Банк предоставил ссуду в размере 50 тыс. грн. на 42 мес. под 16% годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?
По схеме сложных процентов:
По смешанной схеме:.
Таким образом, в данном случае смешанная схема приводит к большей величине наращенной суммы.
При проведении финансовых операций важно знать, как соотносятся между собой величины сумм, наращенных по схеме простых и схеме сложных процентов. Для ответа на этот вопрос сравним множители наращения по простым и сложным процентам, т.е. сравним
1) 2)
Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит: Ø более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода); Ø более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно); Ø обе схемы дают одинаковый результат при продолжительности периода 1 год и однократном начислении процентов. При заключении финансовых контрактов зачастую необходимо определить время, которое необходимо для увеличения первоначальной суммы PV в k раз при заданной доходности r в случае использования схемы простых и схемы сложных процентов: Ø для простых процентов из равенства Ø для сложных процентов из равенства Из этих формул можно, например, найти период, за который происходит удвоение капитала при заданной процентной ставке. Полагая k=2, соответственно получим: В практических расчетах при заключении финансовой сделки для быстрой оценки эффективности предлагаемой ставки процентов при реализации схемы сложных процентов зачастую пользуются приблизительным расчетом периода времени, необходимого для удвоения инвестируемой суммы. С этой целью используются несколько эмпирических приближенных формул: Ø «правило 72». Суть правила заключается в том, что, если – r процентная ставка, выраженная в процентах, то n представляет собой число периодов, за которое исходная сумма приблизительно удвоится. Здесь необходимо обратить внимание на то обстоятельство, что, если в большинстве финансовых расчетов используется процентная ставка, выраженная десятичной дробью, то в алгоритме формулы «правило 72» ставка взята в процентах. Ø «правило 69». Алгоритмом вычисления удвоенной суммы в данном случае является При использовании этих правил необходимо помнить, что при их применении речь идет о периодах начисления процентов и соответствующей данному периоду ставке. Например, если длительностью финансовой операции является половина года, то в расчете должна использоваться полугодовая процентная ставка. Пример. Необходимо определить период времени, в течение которого исходный инвестированный капитал удвоится при процентной ставке, равной 17% годовых.
Ø «правило 72»: Ø «правило 69»: Ø точная формула: Как показывает практика, вышерассмотренные правила хорошо срабатывают для небольших значений процентной ставки, где-то до 20%.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.67.237 (0.008 с.) |

 ;
; ;
;
 - множителем наращения сложных процентов;
- множителем наращения сложных процентов;  - коэффициентом наращения.
- коэффициентом наращения. .
. в зависимости от изменения значений r и n. В этом случае формула алгоритма наращения по схеме сложных процентов трансформируется следующим образом:
в зависимости от изменения значений r и n. В этом случае формула алгоритма наращения по схеме сложных процентов трансформируется следующим образом:
 – мультиплицирующий множитель.
– мультиплицирующий множитель. состоит в следующем: он показывает, чему будет равна одна денежная единица через n периодов при заданной процентной ставке r.
состоит в следующем: он показывает, чему будет равна одна денежная единица через n периодов при заданной процентной ставке r. измеряется в годах, а
измеряется в годах, а  является годовой процентной ставкой. Однако эту формулу можно применять и при других периодах начисления. Необходимо только следить за соответствием длины периода и процентной ставки. Так, если базовым периодом начисления процентов является квартал (месяц), то и в расчетах должна использоваться квартальная (месячная) ставка.
является годовой процентной ставкой. Однако эту формулу можно применять и при других периодах начисления. Необходимо только следить за соответствием длины периода и процентной ставки. Так, если базовым периодом начисления процентов является квартал (месяц), то и в расчетах должна использоваться квартальная (месячная) ставка. - следующие друг за другом временные периоды и на период
- следующие друг за другом временные периоды и на период  установлена процентная ставка
установлена процентная ставка  Тогда, учитывая капитализацию начисленных процентов при использовании схемы сложных процентов, наращенная сумма за время
Тогда, учитывая капитализацию начисленных процентов при использовании схемы сложных процентов, наращенная сумма за время  определяется по формуле:
определяется по формуле:

 тогда формула для определения наращенной стоимости примет вид:
тогда формула для определения наращенной стоимости примет вид: 
 , приводящую к такому же результату, как и с использованием переменных ставок.
, приводящую к такому же результату, как и с использованием переменных ставок.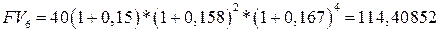 тыс.грн.
тыс.грн. или 10,48%.
или 10,48%. тыс. грн.
тыс. грн.
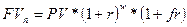
 тыс. грн
тыс. грн тыс. грн.
тыс. грн.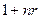 и
и  , если
, если 
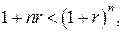
 , если
, если 
 получаем
получаем  :
: получаем
получаем 
 для простых процентов, и
для простых процентов, и  .
. . Заметим, что, как и в предыдущем правиле, размер процентной ставки выражается в процентах.
. Заметим, что, как и в предыдущем правиле, размер процентной ставки выражается в процентах. лет.
лет. года.
года. года.
года.


