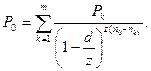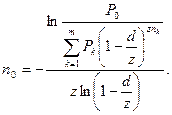Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Консолидация платежей с использованием простой процентной ставки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим теперь задачу замены платежей Рассуждая, как и ранее, можно получить уравнение эквивалентности следующего вида:
Пример. Клиент получил в банке кредит на сумму 3 тыс. грн. под 12% годовых. В соответствии с финансовым контрактом клиент обязался погасить кредит тремя платежами с процентами: 1,5 тыс. грн., 0,5 тыс. грн. и 1 тыс. грн. соответственно через 30, 90 и 150 дней. Однако через некоторое время по обоюдному согласию сторон было решено погасить кредит одним платежом через 120 дней. Необходимо найти величину консолидированного платежа, если начисляются простые проценты.
Найдем платежи с процентами согласно первоначальному соглашению:
Величина консолидированного платежа составит:
Для проверки полученного результата величину консолидированного платежа дисконтируем на момент предоставления кредита:
Срок консолидированного платежа определяется из равенства приведенных стоимостей соответствующих платежей:
Этой формулой можно пользоваться в тех случаях, когда справедливо неравенство:
Пример. Платежи в 2 тыс. грн. и 3 тыс. грн. должны быть погашены соответственно через 45 и 90 дней. Кредитор и должник согласились заменить два платежа одним в 5 тыс. грн. Найти срок оплаты консолидированного платежа, если используется простая процентная ставка 12% годовых и способ 360/360.
следовательно
Если имеет место равенство
Для условий последнего примера с помощью приближенной формулы получим:
Рассмотренные выше формулы для определения консолидированного платежа Р0 и срока n0, конечно, не охватывают все возможные случаи. Например, пять погасительных платежей объединяются в два погасительных платежа; или изменяются сроки платежей без изменения их числа и т.п. Как правило, в каждой конкретной ситуации составляется соответствующее уравнение эквивалентности, отражающее содержание контракта. Причем необходимо оговаривать и некоторые ньюансы, возникающие при составлении этих уравнений. Так, при использовании приведенных значений платежей необходимо согласовывать дату (ее называют базовой), на которую производят приведение. Это делается потому, что от изменения базовой даты в случае простых процентов меняются значения новых искомых характеристик.
Пример. По условию контракта суммы 3тыс. грн., 1 тыс. грн. и 2,5 тыс. грн. должны быть выплачены соответственно 05.05., 15.06. и 25.10. Стороны решили пересмотреть порядок выплат: 3,5 тыс. грн. выплачиваются 01.06.; 1,5 тыс. грн. – 01.07. и остаток долга погашается 10.09. Определить величину третьего платежа, если пересчет осуществляется по простой процентной ставке, равной 15%, по способу 365/365. Все операции проводятся в пределах одного года.
За дату приведения (базовую дату) примем, например, 15.06. – время выплаты 1 тыс. грн. Для лучшего понимания вида уравнения эквивалентности укажем порядковые номера в году представленных в контракте дат: 05.05. – 125; 15.06. – 166; 25.10. – 298; 01.06. – 152; 01.07. – 182; 10.09. – 253. Обозначив остаток долга через Р, запишем уравнение эквивалентности:
Решив это уравнение относительно Р, получим Р = 1,462 тыс. грн.
Замена платежей и сроков их выплат с использованием Сложной процентной ставки. Как и в случае простых процентов, при любой замене платежей с использованием сложных процентов должен выполняться принцип финансовой эквивалентности, соблюдение которого обосновывается составлением соответствующего уравнения. Если платеж Р1 со сроком n1 надо заменить платежом Р0 со сроком n0 при использовании сложной процентной ставки r (причем n1 и n0 измеряются от одного момента времени), то уравнение эквивалентности имеет вид:
Эти три уравнения можно объединить в одно, так как для любых сроков n1 и n0 должно выполняться условие
Отсюда можно сделать следующий вывод: для эквивалентной согласно сложной процентной ставке замены платежей необходимо, чтобы их приведенные стоимости совпадали. Причем расчет приведенных стоимостей можно осуществлять на любой момент времени, так как:
где t – произвольное вещественное число. Таким образом, при сравнении платежей можно выбирать любой удобный или интересующий нас момент времени.
Пример. Платеж в 6 тыс. грн. и сроком уплаты через 4 года заменить платежом со сроком уплаты через: а) 2 года; б) 5 лет. Применяется сложная процентная ставка 12% годовых. а) P1=3, n1= 4, n0= 2, r = 0,12.
б) P1 = 3, n1 = 4, n0 = 5, r =0,12.
Пример. Предлагается выплатить за пользование земельным участком выплатить либо 20 тыс. грн. через 5 лет, либо 30 тыс. грн. через 10 лет. Определить, какое предложение выгоднее, если есть возможность инвестирования денежных средств под сложную процентную ставку 15% годовых. Согласно ранее приведенной формуле можно найти приведенные стоимости платежей на любой момент времени. Предположим, что мы выбрали в качестве момента приведения конец 10-го года. В этом случае наращенная стоимость 20 тыс. грн. через 5 лет составит: Если осуществить приведение платежей, например, к исходному моменту времени, то при учете 20 тыс. грн. за 5 лет и30 тыс. грн. за 10 лет получим соответственно:
Следовательно, опять делаем вывод о предпочтительности первого предложения. Вообще такой вывод будет при выборе любого момента времени для расчета приведенных или наращенных стоимостей платежей, если используется сложная процентная ставка. Однако, если использовать простую процентную ставку и такой же метод оценки предложений, то можно прийти к противоречивым выводам. Так, выбирая конец 10-го года и сравнивая
Если известен размер нового платежа Р0, а необходимо найти срок его выплаты n0, то для этого используется следующая формула:
Пример. Определить величину нового срока, если платеж в 2 тыс. грн. через 5 лет заменяется платежом в 3 тыс. грн. и используется сложная процентная ставка 15% годовых. P1 = 2, n1= 5, P0= 3, r = 0,15.
Рассмотрим более общую ситуацию, когда платежи Р1, Р2, …, Рm, выплачиваемые соответственно через время n1, n2, …, nm, заменяются одним платежом P0 выплатой через время n0. В составляемом уравнении эквивалентности платежу Pk, будет соответствовать слагаемое Уравнение эквивалентности имеет вид:
Если стоит задача сравнения на основании сложной процентной ставки платежа Р0 с заменяемыми платежами, то за момент оценки можно выбирать любой произвольный момент времени. Если известен размер консолидированного платежа, а необходимо найти новый срок его выплаты, то используется формула:
Пример. Три платежа в 3,0, 1,0 и 1,5 тыс. грн. со сроками выплаты соответственно через 1, 2,5 и 4 года заменяются одним платежом, выплачиваемым через 3 года. Найти величину консолидированного платежа, если используется сложная процентная ставка 14% годовых. Какой будет срок выплаты, если консолидированный платеж будет равен сумме исходных платежей?
P1=3, P2= 1, P3=1,5, n1=2, n2=2,5, n3= 4, n0= 3, r = 0,14.
Если же Р0= 3 + 1 + 1,5 = 5,5 тыс. грн., то
Этот же результат можно получить и иначе: считаем, что платеж 6,282 тыс. грн., выплачиваемый через 3 года, необходимо заменить платежом в 5,5 тыс. грн. Тогда новый срок рассчитывается следующим образом:
Если несколько платежей заменяются одним, используется сложная процентная ставка и сложные проценты начисляются z раз, то уравнение эквивалентности имеет вид:
Пример. В условиях предыдущего примера начисление процентов осуществляется ежеквартально. Найти величину консолидированного платежа и новый срок выплаты, если консолидированный платеж будет равен 5,5 тыс. грн.
Существуют различные возможности изменения условий финансового соглашения, поэтому имеется большое многообразие уравнений эквивалентности. Поэтому охватить готовыми формулами все возможные варианты изменения условий финансовых сделок не представляется возможным. Однако в каждой конкретной ситуации при замене платежей уравнение эквивалентности составляется по ранее рассмотренной методике, что подтверждается приведенными примерами. Задача замены платежей при использовании учетной ставки или непрерывных процентов рассматривается аналогичным образом, как и при использовании процентной ставки. Поэтому можно ограничиться приведением основных формул, не останавливаясь подробно на их рассмотрении. Если платежи Р1, Р2, …, Рm, выплачиваемые соответственно через время n1, n2,…, nm, консолидируются в один платеж Р0 с выплатой через время n0 и используется номинальная годовая учетная ставка d, то уравнение эквивалентности имеет следующий вид:
Если необходимо для этих условий определить новый срок выплаты консолидированного платежа, то используется формула:
Тема 7
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.124.24 (0.011 с.) |

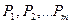 , выплачиваемых соответственно через время
, выплачиваемых соответственно через время  , одним платежом
, одним платежом 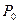 с выплатой через время
с выплатой через время 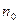 .
.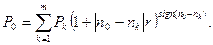
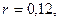
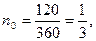

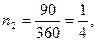
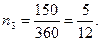

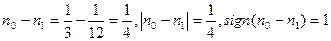
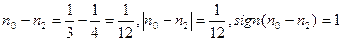
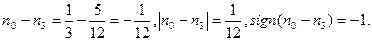
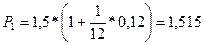 тыс. грн.
тыс. грн. 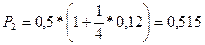 тыс. грн.
тыс. грн.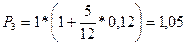 тыс. грн.
тыс. грн.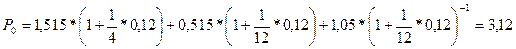 тыс. грн.
тыс. грн.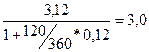 тыс. грн. Это сумма выданного кредита.
тыс. грн. Это сумма выданного кредита.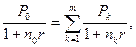 откуда
откуда 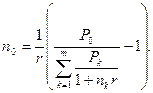
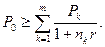
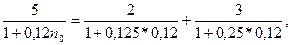
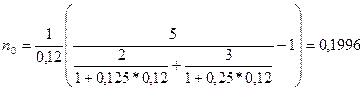 года или» 72 дня.
года или» 72 дня.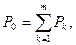 то для определения срока консолидированного платежа используется приближенная формула:
то для определения срока консолидированного платежа используется приближенная формула: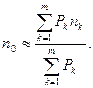
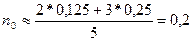 года, или» 72 дня
года, или» 72 дня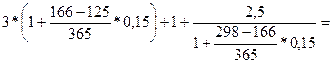
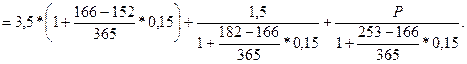
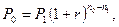 если n0 > n1 ;
если n0 > n1 ;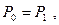 если n0 = n1;
если n0 = n1;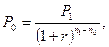 если n0 < n1.
если n0 < n1.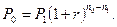 , что равносильно:
, что равносильно: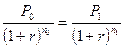 .
.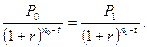
 тыс. грн.
тыс. грн.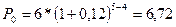 тыс. грн.
тыс. грн.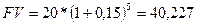 тыс. грн.
тыс. грн. 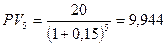 тыс. грн.
тыс. грн. 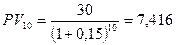 тыс. грн.
тыс. грн.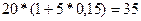 тыс. грн. и 30 тыс. грн. получаем, что первое предложение лучше. Однако, если выберем исходный момент времени и сравним
тыс. грн. и 30 тыс. грн. получаем, что первое предложение лучше. Однако, если выберем исходный момент времени и сравним 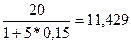 тыс. грн. и
тыс. грн. и 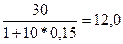 тыс. грн., получаем, что выгоднее второе предложение.
тыс. грн., получаем, что выгоднее второе предложение.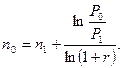

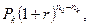 т.е. при n0 > nk, будет иметь место наращение сложных процентов на капитал Pk, а при n0 < n1 капитал Pk будет учитываться.
т.е. при n0 > nk, будет иметь место наращение сложных процентов на капитал Pk, а при n0 < n1 капитал Pk будет учитываться.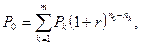 или что то же самое
или что то же самое 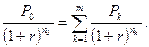
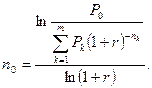
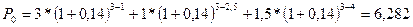 тыс. грн.
тыс. грн.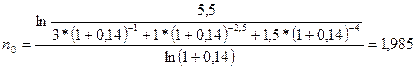 года.
года.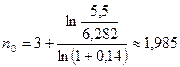 года.
года.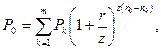 откуда
откуда 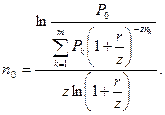
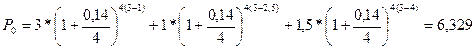 тыс. грн.
тыс. грн.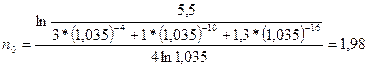 года.
года.