Учет инфляции при использовании схемы простых процентов.

Пусть на капитал PV происходит начисление простых процентов по ставке r в течение времени n и индекс цен за это время равен I_p, тогда учитывая обесценение денег за это время, получим:

 

где представляет собой множитель наращения простых процентов с учетом инфляции.

Из приведенной выше формулы следует, что реальное наращение первоначального капитала с учетом покупательной способности денег будет происходить только в том случае, если Если , то наращение только компенсирует негативное действие инфляции. Из этого выражения следует, что:

Ставка является минимально допустимой процентной ставкой, при которой не происходит реального уменьшения (эрозии) капитала, несмотря на начисление процентов. Эту ставку называют реальной.

Ставка, превышающая , называется положительной процентной ставкой, так как только в этом случае будет происходить реальное увеличение капитала.

Если же полученная наращенная сумма не компенсирует потерю покупательной способности капитала в результате инфляции, то такую банковскую ставку называют отрицательной.

 

Пример. На сумму 5 тыс. грн. в течение трех месяцев начислялись простые проценты по ставке 40% годовых. За каждый месяц цены росли соответственно на 15, 12, и 10%.

Необходимо найти наращенную с учетом инфляции сумму и величину положительной процентной ставки.

 

Индекс цен за квартал составит:

Будущая стоимость с учетом инфляции:

тыс. грн.

При 40% годовых при заданном уровне инфляции реального наращения капитала не будет, а будет, наоборот, иметь место эрозия капитала.

Величина положительной процентной ставки составит:

.

Следовательно, при данном росте цен реальное наращение капитала будет происходить только при ставке, превышающей 166,72%.

 

В целях уменьшения негативного воздействия инфляции и компенсации потерь от снижения покупательной способности денег используются различные методы. Одним из них является индексация процентной ствки, используемой при заключении финансового соглашения. Сущность этого метода заключается в том, что процентная ставка корректируется в соответствии с темпом инфляции. Величина коррекции оговаривается в условиях контракта. Это делается для того, чтобы в условиях инфляции стоимость первоначального капитала действительно увеличивалясь с течением времени.

Такую новую с поправкой на инфляцию ставку называют брутто-ставкой. В этом контексте исходную процентную ставку называют иногда нетто-ставкой.

Для обеспечения полной компенсации негативного дейстия инфляции и получения доходности согласно первоначальной ставке r, определяется размер брутто ставки из равенства:

т.е.

 

Пример. Для условий последнего примера определить брутто-ставку, которая обеспечила бы реальную доходность финансовой операции на уровне 40% годовых.

Проведенные расчеты показывают, что ставка в 223,4% годовых при наращении простыми процентами обеспечивает при заданных условиях реальную доходность в 40% годовых.

Если объявлена норма доходности, т.е. задана брутто-ставка, то из ранее рассмотренного равенства можно определить реальную процентную ставку, т.е. доходность финансовой операции с учетом инфляции при начислении простых процентов:

Таким образом, при инфляции различают следующие виды процентных ставок.

Номинальная процентная ставка – это исходная базовая, как правило, годовая процентная ставка, указанная в договоре. Доходность, выражаемая этой ставкой, не скорректирована на инфляцию.

Реальная процентная ставка – показывает доходность с учетом инфляции Характеризующейся снижением покупательной способности денег. Реальная процентная ставка в условиях инфляции всегда меньше номинальной и может быть даже отрицательной.

Положительная процентная ставка – это любая ставка, при которой будет происходить реальное увеличение стоимости капитала при данном индексе инфляции.

Брутто-ставка – это по существу, любая процентная ставка, превышающая номинальную. Но, как правило, брутто-ставка является положительной процентной ставкой.

Если наращение капитала происходит на основе простой учетной ставки в течение времени и индекс цен за это время равен , то в этом случае величина учетной ставки , компенсирующей инфляционные потери, определяется из равенства:

 

Из этого выражения путем несложных преобразований можно получить:

 

Если задана ставка , то из вышеприведенного равенства можно определить реальную учетную ставку, позволяющую оценить соответствующим образом доходность финансовой операции с учетом инфляции:

 

Пример. Банк выдает клиенту кредит на 2 месяца, в течение которых по оценкам экспертов ежемесячный индекс инфляции составит 1,01.

Необходимо найти значение учетной ставки, компенсирующей потери от инфляции, если банк желает обеспечить реальную доходность, определяемую простой учетной ставкой в 25% годовых.

 

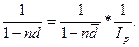
Индекс инфляции за 2 месяца (или за ) составит: .

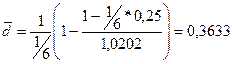или 36,33%.