Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка постоянного аннуитета пренумерандо.Содержание книги
Поиск на нашем сайте Если на денежные поступления начисляются только сложные проценты, то соответствующие расчетные формулы для наращенных сумм аннуитета пренумерандо легко можно вывести из ранее рассмотренных формул для аннуитета постнумерандо. Поскольку денежные поступления в аннуитете пренумерандо происходят в начале каждого периода, то этот аннуитет отличается от аннуитета постнумерандо только количеством периодов начисления процентов. Например, для срочного аннуитета пренумерандо с регулярными денежными поступлениями А и процентной ставкой r, наращенный денежный поток имеет вид:
Следовательно, будущая стоимость аннуитета пренумерандо может быть определена по формуле:
Т.е. наращенная стоимость аннуитета пренумерандо больше в раз наращенной суммы аннуитета постнумерандо. Аналогичным образом можно получить формулы для определения будущей стоимости аннуитета пренумерандо с начислением процентов m раз в течение базового периода и для р-срочных аннуитетов:
Несколько иной будет ситуация в р-срочном аннуитете пренумерандо, когда на взносы, поступающие в течение базового периода, начисляются простые проценты. В отличие от аннуитета постнумерандо в этом аннуитете в каждом периоде любой взнос «действует» еще 1/р –ю часть периода, тем самым доставляя к концу периода дополнительную величину Следовательно, к концу каждого периода взносы, число которых равно р, доставят величину Таким образом, на последнее р-е поступление начисляются простые проценты за часть периода, равную 1/р, и оно будет равно
Таким образом, будущая стоимость аннуитета пренумерандо будет равняться:
В случае начисления только сложных процентов формулы для расчетов приведенных стоимостей пренумерандо имеют вид, аналогичный ранее полученным для аннуитета постнумерандо:
Из приведенных формул понятно, почему в финансовых таблицах не уточняется, какая схема подразумевается в финансовой сделке – постнумерандо или пренумерандо. Содержание таблиц инвариантно к этому фактору. Однако, при применении расчетных формул или финансовых таблиц необходимо строго следить за схемой поступления денежных платежей.
Пример. Ежегодно в начале года в банк делается очередной взнос в размере 10 тыс. грн. Банк платит 20% годовых. Какая сумма будет на счете по истечении трех лет?
Многие практические задачи могут быть решены различными способами в зависимости от того, какой денежный поток выделен аналитиком. Рассмотрим это на следующем примере.
Пример. Вам предложено инвестировать 100 тыс. грн. на срок 5 лет при условии возврата этой суммы частями ежегодно по 20 тыс. грн. По истечении 5 лет выплачивается дополнительное вознаграждение в размере 30 тыс. грн. Следует ли принимать это предложение, если можно депонировать деньги в банк из расчета 12% годовых? Наращенная сумма депонирования:
В отношении альтернативного варианта, предусматривающего возмещение вложенной суммы частями, предполагается, что ежегодные поступления в размере 20 тыс. грн. можно немедленно пускать в оборот, получая дополнительные доходы. Если нет других альтернатив по эффективному использованию этих сумм, их можно депонировать в банк. В этом случае денежный поток можно представить двояко: а) как срочный аннуитет постнумерандо с параметрами: А= 20, n = 5, r = 20% и единовременное получение 30 тыс. грн. в конце периода:
б) как срочный аннуитет пренумерандо с параметрами: А = 20, n = 4, r = 20% и единовременное получение сумм в 30 и 20 тыс. грн. в конце финансовой операции:
Таким образом, предложение экономически нецелесообразно.
Бессрочный аннуитет. Аннуитет считается бессрочным, если денежные поступления продолжаются достаточно длительное время. Математически это означает, что Определение будущей стоимости бессрочного аннуитета, естественно, не имеет смысла. Что же касается обратной задачи (определение приведенной стоимости), то она имеет вполне определенное решение. Поток платежей в постоянном бессрочном аннитете при одном денежном поступлении А за период, являющися базовым для начисления процентов по ставке r, представляет собой бесконечно убывающую геометрическую прогрессию с первым членом
где Приведенная формула показывает, что поток даже с неограниченным числом платежей имеет все же конечную приведенную стоимость. С финансовой точки зрения это вполне понятно, поскольку деньги, которые поступят через много лет, сейчас мало что стоят, а при высокой инфляции и ничего не стоят. Эта же ситуация проявляется и при сравнении коэффициентов дисконтирования бессрочного аннуитета и аннуитетов с большим сроком Для сравнения приведем в таблице значения FM4(r,n) при r = 10%.
Из приведенной таблицы видно, что при сроке аннуитета, превышающем 50 лет, коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга. Кроме того, с ростом процентной ставки величина срока, начиная с которого величина факторного множителя FM4(r,n) перестают сильно отличаться друг от друга, уменьшается. Например, при r = 15% такой срок равняется 40 годам. Таким образом, при больших сроках аннуитета и большом уровне процентной ставки для определения приведенной стоимости срочного аннуитета можно воспользоваться формулой для определения приведенной стоимости бессрочного аннуитета, при этом полученный приблизительный результат будет не слишком отличаться от точного значения. Приведенная формула используется для оценки целесообразности приобретения бессрочного аннуитета, если известен размер денежного поступления за период. В качестве r обычно принимается гарантированная процентная ставка, например, предлагаемая государственным банком.
Пример. Необходимо определить текущую стоимость бессрочного аннуитета постнумерандо с ежегодным поступлением 4,2 тыс. грн., если предлагаемый государственным банком процент по срочным вкладам равен 14% годовых.
Следовательно, если аннуитет предлагается по цене, не превышающей 30 тыс. грн., то инвестирование в него будет представлять выгодную для инвестора операцию. С помощью вышеприведенной формулы можно определить истинную стоимость обыкновенной акции в том случае, когда выплачиваются одинаковые дивиденды (равные А) в течение всего времени финансовой операции. При этом предположении темп ростов дивидендов равен нулю и соответствующая модель называется моделью нулевого роста. Такая ситуация в определенном смысле свойственна привилегированным акциям высокого качества, выплаты дивидендов по которым одинаковы, регулярны и не зависят от величины прибыли на одну акцию, а время обращения привилегированных акций не ограничено. Пример. Компания гарантирует выплату дивидендов в размере 6 тыс. грн. Имеет ли смысл покупать акции этой компании в течение неопределенно долгого времени по цене 35 тыс. грн., если можно поместить деньги на депозит под 15% годовых? Из формулы Приведенная стоимость бессрочного аннуитета постнумерандо с денежными поступлениями р раз за базовый период и начислением сложных процентов m - раз за период может быть получена из следующей формулы:
Пример. Фирма собирается учредить фонд для ежегодной (в конце года) выплаты пособий своим работникам. Необходимо определить сумму, которую фирма должна поместить на депозит в банк, чтобы обеспечить получение неограниченно долго в конце каждого года 8 тыс. грн., если банк начисляет: а) ежегодно сложные проценты по ставке 16%; б) ежеквартально сложные проценты по ставке 14%; в) непрерывные проценты с силой роста 13,5%.
Во всех трех случаях денежный поток является бессрочным аннуитетом постнумерандо. Необходимо найти приведенную стоимость такого аннуитета. а)
б)
в)
Приведенная стоимость бессрочного аннуитета пренумерандо в общем виде определяется с помощью приведенной стоимости бессрочного аннуитета постнумерандо по следующей формуле:
Следовательно, приведенная стоимость бессрочного аннуитета пренумерандо отличается от таковой для аннуитета постнумерандо на величину первого платежа.
Непрерывный аннуитет. Предположим, что в течение каждого периода времени денежные поступления происходят очень часто, так что промежутки между последовательными поступлениями представляют собой бесконечно малые величины. В этом случае аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью: одно и то же количество денежных единиц в единицу времени. Соотношения, характеризующие непрерывный аннуитет, можно вывести из формул для р-срочного аннуитета, переходя в них к пределу при Ясно, что непрерывно не может поступать величина А, так как через любой малый промежуток времени накопится бесконечно большая сумма денег. Пусть в конце каждого периода р-срочного аннуитета суммарная величина денежных поступлений составит
Приведенная стоимость непрерывного аннуитета рассчитывается по формуле:
В течение 6 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя 40 тыс. грн. Определить сумму, накопленную к концу шестого года при использовании процентной ставки 12% годовых.
Считая, что платежи поступают непрерывным образом, рассчитаем будущую стоимость непрерывного аннуитета:
Эта же задача может быть решена иначе, если примем р = 360, а А = 40/360:
Выполнив расчет видим, что результаты вычислений по двум формулам привели практически к одинаковому результату. Если проценты начисляются раз за период, то пользуются формулой:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

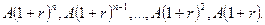



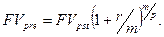
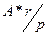 .
.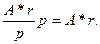
 предпоследнее (р – 1)-е поступление станет равным
предпоследнее (р – 1)-е поступление станет равным  и т.д. вплоть до первого поступления, которое станет равным
и т.д. вплоть до первого поступления, которое станет равным 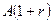 . Следовательно, сумма этих величин, образующих арифметическую прогрессию, равна:
. Следовательно, сумма этих величин, образующих арифметическую прогрессию, равна:
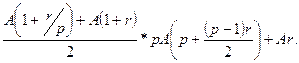
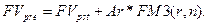
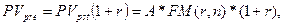
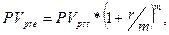
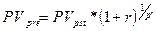
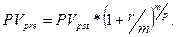
 тыс. грн.
тыс. грн.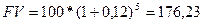 тыс. грн.
тыс. грн.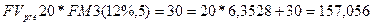 тыс. грн.
тыс. грн.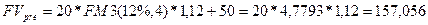 тыс. грн.
тыс. грн.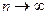 . Характерным примером бессрочного аннуитета являются консоли – выпускаемые правительствами некоторых стран облигации, по которым производят регулярные купонные выплаты, но которые не имеют фиксированного срока. В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет также называют вечной рентой.
. Характерным примером бессрочного аннуитета являются консоли – выпускаемые правительствами некоторых стран облигации, по которым производят регулярные купонные выплаты, но которые не имеют фиксированного срока. В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет также называют вечной рентой. и знаменателем
и знаменателем 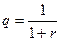 . Для бессрочного аннуитета постнумерандо формула для определения приведенной стоимости имеет вид:
. Для бессрочного аннуитета постнумерандо формула для определения приведенной стоимости имеет вид:
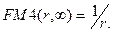
 тыс. грн.
тыс. грн.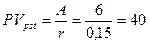
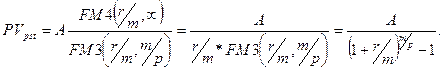
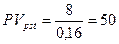 тыс. грн.
тыс. грн.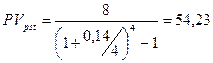 тыс. грн.
тыс. грн.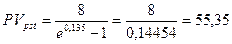 тыс. грн.
тыс. грн.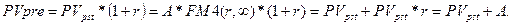
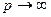 и несколько модифицируя величину члена аннуитета.
и несколько модифицируя величину члена аннуитета.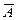 , тогда каждое поступление будет равняться
, тогда каждое поступление будет равняться 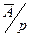 и ранее рассмотренная формула
и ранее рассмотренная формула 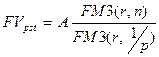 может быть использована для оценки будущей стоимости непрерывного аннуитета:
может быть использована для оценки будущей стоимости непрерывного аннуитета:
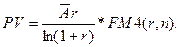
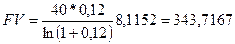 тыс. грн.
тыс. грн.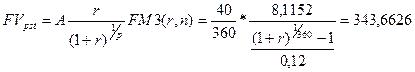 тыс. грн.
тыс. грн.