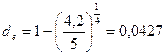Эффективная годовая процентная ставка.

Различные виды финансовых контрактов могут предусматривать различные схемы начисления процентов. Как правило, в этих контрактах обычно оговаривается номинальная процентная ставка, которая не принимает во внимание изменение стоимости денег в связи с инфляцией.

Номинальная процентная ставка имеет следующие недостатки:

1) она не отражает реальной эффективности сделки;

2) в связи с этим она не может быть использована для сопоставления эффективности различных инвестиционных проектов.

Поэтому, для обеспечения сравнительного анализа эффективности таких контрактов применяется другой показатель, который является универсальным для любой схемы начисления процентов.

Таким показателем является эффективная годовая процентная ставка , которая обеспечивает переход от PV к FV при заданной годовой процентной ставке и однократным начислением процентов.

Общая постановка задачи формулируется следующим образом.

Задана исходная сумма PV, номинальная процентная ставка r и количество начислений сложных процентов m.

Естественно, что этому набору исходных величин в рамках одного года соответствует вполне определенное значение будущей стоимости FV.

Требуется найти такую годовую ставку , которая обеспечила бы точно такое же наращение, как и исходная схема, но при m = 1. Т.е. обе схемы должны быть равносильными.

В рамках одного года

Из определения годовой эффективной ставки вытекает, что:

, откуда .

Разделив обе части равенства на PV получим:

. Откуда .

Из полученной формулы видно, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку. Эти две ставки совпадают при m = 1. Именно годовая эффективная процентная ставка является критерием эффективности финансовых операций и может быть использована для пространственно-временных сопоставлений.

Пример.

Предприниматель может получить ссуду на следующих условиях:

а) либо исходя из ежемесячного начисления процентов по номинальной процентной ставке 26% годовых;

б) либо исходя из полугодового начисления из расчета 27% годовых.

Какой вариант предпочтительнее?

а)

б)

 

Так как эффективная годовая процентная ставка характеризует относительные расходы предпринимателя по обслуживанию ссуды, то вариант б) для предпринимателя более предпочтителен. Необходимо также отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель – эффективная процентная ставка.

Понимание роли эффективной процентной ставки чрезвычайно важно для финансового менеджера. Дело в том, что принятие решения о привлечении средств, например банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предполагаемой процентной ставки, которая в этом случае характеризует относительные расходы заемщика. В рекламных проспектах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма существенно отличаться от эффективной ставки.

Пример.

Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%.

M
	0,10	0,1025	0,10381	0,10471	0,10516

 

Различие между двумя ставками может быть гораздо более может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например, при оформлении кредита на условиях добавленного процента.

В финансовых соглашениях не имеет значения, какую из ставок указывать – эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку. В европейских странах, как правило, вначале определяется эффективная ставка, а затем используется формула .

Если в контракте указаны эффективная ставка и количество начислений сложных процентов, а необходимо найти номинальную ставку, то используется формула:

.

Пример.

Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно.

.

Таким образом, ежегодное начисление сложных процентов по ставке 18% годовых дает какой же результат, что и ежемесячное начисление сложных процентов по ставке 16,67%.

Если две номинальные годовые процентные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными.

Пример.

Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если соответствующая им эффективная ставка равна 20%?

для полугодового начисления ;

для ежеквартального начисления .

Таким образом, номинальные ставки 19,09% и 18,65% являются эквивалентными.

Мы рассмотрели наиболее стандартный и широко распространенный подход к понятию эффективной ставки.

Однако, возможны и другие подходы, которые вытекают из разнообразия финансовых соглашений. Например, вполне реальна ситуация, когда условия начисления процентов меняются: в частности, после схемы сложных процентов начиная с какого то момента времени начинают использовать схему простых процентов без прерывания действия контракта. Для анализа таких ситуаций может быть предложен следующий подход к нахождению эффективной процентной ставки. Пусть известна первоначальная сумма PV и наращенная каким либо образом за время n сумма FV. Тогда по определению:

и поэтому .

Пример.

В долг на 2,5 года предоставлена сумма в 30 тыс. грн. с условием возврата 40 тыс. грн. Найти эффективную ставку в этой финансовой сделке.

или 12,196%.

Проверим полученный результат. Предположим в банк помещен вклад в размере 30 тыс. грн. на 2,5 года под 12,196% годовых сложных процентов. Тогда наращенная сумма будет равна:

тыс. грн.

Как и в случае процентной ставки можно также определить эффективную годовую учетную ставку . Она обеспечивает переход от к при заданных значениях этих параметров и однократном дисконтировании в течение года.

Поскольку согласно определению в рамках одного года

, то после соответствующих преобразований получим: .

Из приведенной формулы следует, что с ростом количества начислений величина годовой учетной ставки уменьшается.

Зная годовую учетную ставку можно определить коэффициент дисконтирования: .

Используя можно определить эквивалентные номинальные учетные ставки.

Эффективную годовую учетную ставку можно определить иначе, если известна величина , и дисконтированная каким-либо образом за время сумма .

В этом случае , откуда .

Пример.

Долговое обязательство равное 5 тыс. грн. со сроком погашения 4 года было сразу же учтено в банке и владелец обязательства получил 4,2 тыс. грн.

Найти эффективную годовую учетную ставку.

Тема 4