Аннуитет с изменяющейся величиной платежа.

На практике возможны ситуации, когда величина платежа меняется со временем в сторону увеличения или уменьшения. Например, при заключении договора аренды в условиях инфляции может предусматриваться периодическое увеличение платежа, компенсирующее негативное влияние изменения цен. Или другой пример, когда величина амортизационных отчислений может меняться в связи с изменением количества и стоимости основных фондов.

В таких ситуациях поток платежей представляет собой переменный аннуитет (переменную ренту) и для определения будущей или приведенной стоимости необходимо пользоваться ранее рассмотренными формулами для переменного аннуитета. Однако, когда члены аннуитета изменяются в соответствии с некоторыми законами, эти формулы существенно могут быть упрощены.

Предположим, что имеется аннуитет постнумерандо, платежи которого образуют арифметическую прогрессию с первым членом А и разностью z.

В этом случае говорят о переменном аннуитете с постоянным абсолютным изменением его членов. Если число периодов равно n, а r является процентной ставкой за базовый период, в соответствии с которой один раз в конце периода начисляются сложные проценты и период аннуитета совпадает с базовым, то наращенный денежный поток, записанный в порядке поступления платежей имеет вид:

Если z >0, то члены аннуитета возрастают. Если z <0, члены аннуитета убывают и число этих членов должно удовлетворять равенству n < 1 – A/z, иначе можно получить отрицательные платежи, что лишено смысла.

Сложив наращенные члены аннуитета и сгруппировав отдельно слагаемые, содержащие множители А и z, получим:

 

Из этого выражения с помощью определенных преобразований получаем формулы для определения будущей и приведенной стоимости такого аннуитета:

 

Пример.

Согласно условиям финансового соглашения на счет в банке в течение 6 лет в конце года будут поступать денежные суммы, первая из которых равна 5 тыс. грн., а каждая последующая будет увеличиваться на 0,4 тыс. грн.

Необходимо оценить аннуитет, если банк применяет процентную ставку 10% годовых и сложные проценты начисляются один раз в конце года.

Как изменятся оценки аннуитета, если денежные суммы будут уменьшаться на 0,4 тыс. грн.?

а) для условия возрастания членов аннуитета:

тыс.грн.

 

тыс. грн.

б) для условия уменьшения членов аннуитета:

тыс. грн.

тыс. грн.

Для оценки аннуитетов пренумерандо используются следующие формулы:

 

Аналогичным образом можно получить оценки аннуитета для других ситуаций, например, для случая, если в указанных выше условиях начисление сложных процентов происходит раз за базовый период:

 

Пример.

В условиях предыдущего примера определить будущую стоимость аннуитета, если начисление сложных процентов происходит в конце каждого полугодия.

тыс.грн.

 

Из формул для определения будущей и приведенной стоимости аннуитета можно определить величину аннуитета А и разность z:

 

Что касается процентной ставки и продолжительности аннуитета, то формулы для их определения в явном виде не могут быть получены. Поэтому для определения этих параметров используются приближенные методы.

 

Пример.

За 10 лет необходимо накопить 60 тыс. грн. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 300 грн. и процентная ставка равна 15% годовых? Денежные поступления и начисление сложных процентов осуществляются в конце года.

Определить, на какую величину необходимо увеличивать каждый год денежное поступление, если первый вклад будет равен 2,5 тыс. грн.?

 

тыс.грн.

тыс. грн.

 

Предположим, что платежи в аннуитете образуют геометрическую прогрессию с первым членом А и знаменателем q.

В этом случае имеет место переменный аннуитет с постоянным относительным изменением его членов.

Если r является процентной ставкой за базовый периолд, совпадающий с периодом аннуитета, n равно числу периодов и в конце каждого периода начисляются сложные проценты, то наращенный денежный поток имеет вид:

Представленная последовательность чисел представляет собой геометрическую прогрессию с первым членом и знаменателем . Поэтому будущая стоимость такого аннуитета будет равна:

 

Приведенная стоимость аннуитета определяется по формуле:

 

Пример.

По условиям контракта на счет в банке поступают в течение 5 лет в конце года платежи. Первый платеж равен 3 тыс. грн., а каждый следующий год по отношению к предыдущему увеличивается на 15%

Необходимо оценить такой аннуитет, если банк начисляет в конце каждого года сложные проценты из расчета 12% годовых.

 

Увеличение платежа на 15% означает его рост в1,15 раза, т.е. поток платежей образует геометрическую прогрессию с знаменателем q =1,15.

тыс. грн.

тыс. грн.

 

Используя вышеприведенные формулы для расчета будущей и приведенной стоимости аннуитета можно напистаь в явном виде формулы для определения только величины аннуитета:

 

Что касается знаменателя геометрической прогрессии, процентной ставки и продолжительности аннуитета, то эти параметры могут быть определены только с помощью приближенных методов.

Если же члены переменного аннуитета не образуют ни арифметическую, ни геометрическую прогрессию, то, тем не менее, во многих случаях оценка таких аннуитетов может быть выполнена с помощью финансовых таблиц. Рассмотрим технику подобных вычислений на следующем примере.

 

Пример.

Садовый участок сдается в аренду на 10 лет. Арендная плата будет осуществляться ежегодно по схеме постнумерандо на следующих условиях: в первые шесть лет – по 10 тыс. грн., а в оставшиеся четыре года – по 11 тыс. грн.

Требуется оценить приведенную стоимость этого договора, если процентная ставка, используемая аналитиком, равна 15%.

 

Решать данную задачу можно различными способами, в зависимости от того, какие аннуитеты будут выделены аналитиком.

Ествественн, приведенная стоимость денежного потока должна оцениваться с позиции начала первого временного интервала.

Рассмотрим два возможных варианта. Оба варианта основываются на свойстве аддитивности рассмотренных алгоритмов в отношении величины аннуитетного платежа.

1) Исходный поток можно представить как сумму двух аннуитетов: первый имеет А = 10 тыс. грн. и продолжается 10 лет, второй имеет А = 1 тыс. грн. и продолжается четыре года.

По формуле оцениваем приведенную стоимость каждого аннуитета. Однако второй аннуитет в этом случае будет оценен с позиции начала седьмого года. Поэтоому полученную сумму необходимо дисконтировать с помощью формулы к началу первого года. В этом случае оценки двух аннуитетов будут приведены к одному моменту времени, а их сумма даст оценку приведенной стоимости исходного денежного потока:

тыс. грн.

2) Исходный поток можно представить как разность двух аннуитетов: первый имеет А = 11 тыс. грн. и продолжается десять лет; второй имеет А = 1 тыс. грн. и, начавшись в первом году, заканчивается в шестом. В этом случае расчет выглядит так:

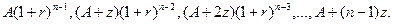
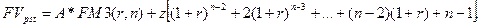
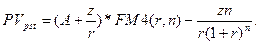
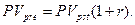
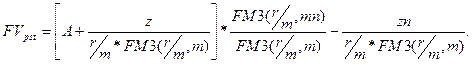
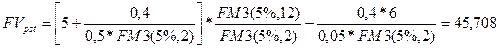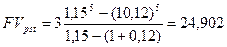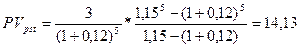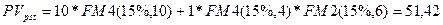тыс. грн.