
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наращение и дисконтирование с использованием схемы простых процентовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема 2 Наращение и дисконтирование с использованием схемы простых процентов
Основу коммерческих вычислений составляют ссудно-заемные операции, в которых и проявляется, прежде всего, необходимость учета временной стоимости денег. Несмотря на то, что в основе расчетов заложены простейшие вычислительные схемы, эти расчеты весьма многообразны, так как предусматривают различные условия контрактов, частоту и способы начислений, различные варианты предоставления и погашения ссуд. Рассмотрев операции наращения, можно увидеть, что, предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы дискретного начисления: 1) схема простых процентов; 2) схема сложных процентов. По отношению к моменту времени начисления или выплаты проценты делятся на обычные и авансовые. Обычные (заемные, декурсивные, postnumerando) проценты начисляются в конце периода финансовой операции. Авансовые (антисипативные, дисконтные, учетные, prenumerando) начисляются в начале периода. Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Если исходный инвестируемый капитал равен PV, а требуемая доходность в долях единицы составляет r, то считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину PV* r. Таким образом, через n лет размер инвестированного капитала будет равен: FV = PV + PV*r + … + PV*r = PV + PV*n*r = PV*(1 +n* r) Из приведенной формулы видно, что проценты начисляются на одну и ту же величину капитала в течение всего срока. Это выражение называется формулой наращения простыми процентами, а множитель (1 + n*r) – множителем наращения или коэффициентом наращения простыми процентами. Из приведенной формулы видно, что приращение капитала составляет величину PV*n*r, оно пропорционально сроку ссуды и ставке процента и растет линейно вместе с ростом n. Величину PV*n*r часто называют процентным платежом. Необходимо обратить внимание на размерность величин, определяющих размер процентного платежа. Размерности n и r всегда должны быть согласованы. Таким образом, либо n должно измеряться в годах, либо с изменением размерности n (например, не годы, а кварталы) ставка процента должна отражать рост за новую единицу времени (за квартал). Исходя из сказанного наращение по простым процентам в случае, если продолжительность финансовой операции не равна целому числу лет (например, меньше года), определяется по формуле:
где t – продолжительность финансовой операции в днях; Т - количество дней в году. Наращение по простым процентам применяется при обслуживании депозитных вкладов с ежемесячной выплатой процентов, и вообще в тех случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются вкладчику. Простые проценты применяют и при выдаче широко распространенных краткосрочных ссуд, т.е. ссуд, предоставляемых на срок до одного года с однократным начислением процентов. При использовании схемы простых процентов частота начисления не оказывает никакого влияния на суммарную величину процентных денег. Пример Клиент поместил в банк вклад в сумме 35 тыс. грн. под 15 % годовых. Какова будет суммарная величина процентных денег, если: а) проценты будут начисляться один раз в конце года; б) проценты будут начисляться ежемесячно? В первом случае FV – PV = 35* 0,15* 1 год = 5,25 тыс. грн. Во втором случае FV – PV = 35* 1/12* 0,15 = 437,5 грн. Т.е. во втором случае суммарный годовой доход клиента в виде начисленных процентов составит те же 437,5* 12 = 5,25 тыс. грн. При определении продолжительности финансовой операции принято день выдачи и день погашения ссуды считать одним днем. В зависимости от того, чему принимается равной продолжительность периода сделки (год, квартал, месяц), размер промежуточной процентной ставки может быть различным. Возможны следующие варианты: 1) точный процент (exact interest), определяемый исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31); 2) обыкновенный процент (ordinary interest), определяемый исходя из приближенного числа дней в году, квартале, месяце (соответственно, 360, 90, 30). При определении продолжительности периода, на который выдана ссуда, также возможны два варианта: 1) в расчет принимается точное число дней, на которое выдана ссуда; 2) в расчет принимается приближенное число дней, не которое выдана ссуда (исходя из продолжительности месяца 30 дней). Исходя из сказанного, расчет может выполняться одним из трех способов: 1) Точный процент с точным числом дней. Этот вариант дает самые точные результаты (Великобритания, США). Обозначение 365/365, ACT/ACT. 2) Обыкновенный процент с точным числом дней. Этот метод иногда называют банковским (Banker’s Rule), распространен в ссудных операциях коммерческих банков, в частности во Франции, Бельгии. Этот вариант дает несколько больший результат, чем применение точных процентов. При числе дней ссуды, превышающем 360, данный способ приводит к тому, что сумма начисленных процентов будет больше, чем предусматривается годовой ставкой. Например, если t=364, то n=364/360=1,011. Обычно это условие финансовой сделки обозначается как 365/360, ACT/360. 3) Обыкновенный процент с приближенным числом дней. Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в коммерческих банках Германии. Обозначение в условиях финансовой сделки 360/360, или немецкая практика; Вариант с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется. Величина эффекта от выбора того или иного способа зависит от размеров суммы, фигурирующей в процессе финансовой операции. Пример. Банк выдал кредит 20.01. в размере 500 тыс. грн. Срок возврата кредита 05.10. Процентная ставка установлена в размере 15% годовых. Год не високосный. Точное число дней (по таблице) = 278 - 20 = 258 дня. Приближенное число дней = 12 дней января + 30 дней февраля + 30 дней марта + 30 дней апреля + 30 дней мая + 30 дней июня + 30 дней июля + 30 дней августа + 30 дней сентября + 5 дней октября – 1 день = 256 дней. Ø точный процент и точное число дней
Ø обыкновенный процент и точное число дней
Ø обыкновенный процент и приближенное число дней
Между величинами процентного дохода, рассчитанными с использованием различной временной базы, при равной продолжительности ссуды существуют следующие соотношения:
Эти соотношения могут быть использованы при определении эквивалентных процентных ставок, то есть ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах:
В мировой практике при расчете процента используют и другие величины. Пусть
В этих формулах – – Естественно, что при одной и той же ставке Дивизор численно равен такому количеству денежных единиц, с которого при ставке процента Если PV = Пример. Вычислить процент с капитала в 2,4 млн. грн., отданного в долг по ставке 16% годовых на срок с 05.03. по 21.09. того же года, если расчет ведется способом 365/365. t = 264 –64 = 200 дней. D = 365/0,16 = 2281,25 I = 2,4*200/2281,25 = 0,210411 млн. грн. Проверим: FV = 2281.25*(1 + 200/365*0,16) = 2481.25 грн. Доход от операции 2481.25 – 2281.25 = 200 грн. за 200 дней или 1 грн. дохода за день финансовой операции (что и требовалось доказать).
Тема 3 Пример. В банк вложены деньги в сумме 5 тыс. грн. на два года с полугодовым начислением процентов под 20% годовых.
Пример. В условиях предыдущего примера проанализирвать, изменится ли величина капитала к концу двухлетнего периода, если проценты будут начисляться ежеквартально.
Из приведенных примеров можно сделать два простых практических вывода: Ø при начислении сложных процентов 12% годовых не эквивалентны 1% в месяц; Ø чем чаще идет начисление по схеме сложных процентов, тем больше накопленная сумма. В зависимости от частоты начисления процентов, наращение суммы осуществляется различными темпами, причем с возрастанием частоты начисленная сумма увеличивается. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала. Что же касается темпа прироста накопленной суммы, то с ростом частоты начисления процентов она постепенно уменьшается. Пример. Рассчитать накопленную сумму для различных вариантов начисления сложных процентов за один год, если исходная сумма равняется 1000 грн. а годовая процентная ставка 10%.
При заключении финансовых контрактов возможны случаи, в которых начисление процентов осуществляется по внутригодовым подпериодам и продолжительность общего периода действия контракта не равна целому числу подпериодов. В этом случае также возможно использование двух схем: Ø схема сложных процентов: 2) по смешанной схеме: где:
Пример. Банк предоставил ссуду в размере 120 тыс. грн. на 27 месяцев под 16% годовых на условиях единовременного возврата основной суммы долга и начисленных процентов. Проанализировать, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) годовое; б) полугодовое; в) квартальное. Годовое начисление процентов. Ø схема сложных процентов: Ø смешанная схема: Полугодовое начисление процентов. В этом случае мы имеем дело с ситуацией, когда начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. Значит, решаем задачу с параметрами:
Ø схема сложных процентов: Ø смешанная схема: Квартальное начисление процентов. В этом случае параметры задачи:
Пример. Что выгоднее: получить2,8 тыс. грн. через 3 года, или 2,9 тыс. грн. через 4 года, если можно поместить деньги на депозит под сложную процентную ставку 10% годовых? Задача решается с позиции текущего момента.
Значит, с позиции текущего момента выгоднее получить 2,8 тыс. грн. через 3 года, т.к. 2,104 тыс. грн. больше, чем 1,981 тыс. грн. Пример. Долговое обязательство на выплату 20 тыс. грн. со сроком погашения 4 года учтено за 2 года до срока с дисконтом по сложной учетной ставке 8% годовых. Найти величину дисконта.
Если срок, за который осуществляется дисконтирование, не является целым числом лет, то возможны следующие методы определения стоимости учтенного капитала: Ø использование сложной учетной ставки:
Ø использование смешанной схемы:
где w – целое число лет; f - дробная часть года.
Пример. Долговое обязательство на выплату 20 тыс. грн. со сроком погашения 4 года учтено за 27 месяцев до срока с дисконтом по сложной учетной ставке 8% годовых. Найти величину дисконта.
Если сравнивать между собой дисконтирование по простой и сложной учетным ставкам, то, для лица, осуществляющего предварительное (антисипативное) начисление процентов: Ø более выгодным является дисконтирование по сложной учетной ставке, если срок учета менее одного года; Ø более выгодным является дисконтирование по простой учетной ставке, если срок учета превышает один год; Ø дисконтирование в обоих случаях дает один и тот же результат, если срок учета равен одному году. Если дисконтирование происходит m раз в году и задана сложная годовая учетная ставка d, то определение стоимости капитала, учтенного за n лет при m–кратном дисконтировании в течение года определяется по формуле:
Пример. Долговое обязательство на выплату 3 тыс. грн. со сроком погашения 5 лет учтено за 2 года до срока. Определить полученную сумму, если производилось: а) полугодовое; б) поквартальное дисконтирование по номинальной учетной ставке 12% годовых. а) б)
Если антисипативное начисление процентов (или дисконтирование) осуществляется по внутригодовым подпериодам, но общий период не равен целому числу подпериодов, то для этой цели используются следующие формулы:
Пример. Определить современное значение суммы в 4 тыс. грн., если они будут выплачены через 2 года и 3 месяца и дисконтирование производилось по полугодиям по номинальной годовой учетной ставке 10%. Полагаем n = 2,25, m = 2, w = 2*2,25 = 4,5 = 4, f = 4,5 – 4 = 0,5.
Если необходимо определить время до срока погашения долгового обязательства, то используются следующие формулы:
Пример. За долговое обязательство в 30 тыс. грн. банком было выплачено 20 тыс. грн. За какое врямя до срока погашения было учтено это обязательство, если банком использовалась годовая сложная учетная ставка 8%?
Если необходимо определить величину номинальной учетной ставки при известных значениях остальных параметров финансовой операции, то необходимо пользоваться формулами:
Пример. Вексель был учтен за полтора года до срока, при этом владелец векселя получил 0,8 от написанной на векселе суммы. По какой сложной годовой учетной ставке был учтен вексель? Поскольку PV = 0,8FV, то Часто встречаются ситуации, когда условиями контракта предусматриваются плавающие учетные ставки. Пусть на периоды времени
Обозначим Таким образом, на все время можно установить вместо плавающих учетных ставок среднюю учетную ставку, которая обеспечит такой же результат. Вышеприведенной формулой можно пользоваться и в случае, когда периоды времени выражены в различных единицах при условии согласования их размерностей с размерностями соответствующих учетных ставок. Пример. Вклад в размере 1000 грн. положен в банк сроком на 7 лет, причем предусмотрен следующий порядок начисления сложных процентов по плавающей учетной ставке: в первые два года – 8%, в последующие 4 года – 12%, а в оставшийся год – 15%. Найти наращенную сумму.
Пример. Предприниматель может получить ссуду на следующих условиях: а) либо исходя из ежемесячного начисления процентов по номинальной процентной ставке 26% годовых; б) либо исходя из полугодового начисления из расчета 27% годовых. Какой вариант предпочтительнее? а) б)
Так как эффективная годовая процентная ставка характеризует относительные расходы предпринимателя по обслуживанию ссуды, то вариант б) для предпринимателя более предпочтителен. Необходимо также отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель – эффективная процентная ставка. Понимание роли эффективной процентной ставки чрезвычайно важно для финансового менеджера. Дело в том, что принятие решения о привлечении средств, например банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предполагаемой процентной ставки, которая в этом случае характеризует относительные расходы заемщика. В рекламных проспектах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма существенно отличаться от эффективной ставки. Пример. Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%.
Различие между двумя ставками может быть гораздо более может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например, при оформлении кредита на условиях добавленного процента. В финансовых соглашениях не имеет значения, какую из ставок указывать – эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же наращенную сумму. В США в практических расчетах применяют номинальную ставку. В европейских странах, как правило, вначале определяется эффективная ставка, а затем используется формула Если в контракте указаны эффективная ставка и количество начислений сложных процентов, а необходимо найти номинальную ставку, то используется формула:
Пример. Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно.
Таким образом, ежегодное начисление сложных процентов по ставке 18% годовых дает какой же результат, что и ежемесячное начисление сложных процентов по ставке 16,67%. Если две номинальные годовые процентные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными. Пример. Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если соответствующая им эффективная ставка равна 20%? для полугодового начисления для ежеквартального начисления Таким образом, номинальные ставки 19,09% и 18,65% являются эквивалентными. Мы рассмотрели наиболее стандартный и широко распространенный подход к понятию эффективной ставки. Однако, возможны и другие подходы, которые вытекают из разнообразия финансовых соглашений. Например, вполне реальна ситуация, когда условия начисления процентов меняются: в частности, после схемы сложных процентов начиная с какого то момента времени начинают использовать схему простых процентов без прерывания действия контракта. Для анализа таких ситуаций может быть предложен следующий подход к нахождению эффективной процентной ставки. Пусть известна первоначальная сумма PV и наращенная каким либо образом за время n сумма FV. Тогда по определению:
Пример. В долг на 2,5 года предоставлена сумма в 30 тыс. грн. с условием возврата 40 тыс. грн. Найти эффективную ставку в этой финансовой сделке.
Проверим полученный результат. Предположим в банк помещен вклад в размере 30 тыс. грн. на 2,5 года под 12,196% годовых сложных процентов. Тогда наращенная сумма будет равна:
Как и в случае процентной ставки можно также определить эффективную годовую учетную ставку Поскольку согласно определению в рамках одного года
Из приведенной формулы следует, что с ростом количества начислений величина годовой учетной ставки уменьшается. Зная годовую учетную ставку можно определить коэффициент дисконтирования: Используя Эффективную годовую учетную ставку можно определить иначе, если известна величина В этом случае Пример. Долговое обязательство равное 5 тыс. грн. со сроком погашения 4 года было сразу же учтено в банке и владелец обязательства получил 4,2 тыс. грн. Найти эффективную годовую учетную ставку.
Тема 4 Аннуитет. Одним из ключевых понятий в финансовых расчетах является понятие аннуитета. Аннуитет – это частный случай денежного потока, а именно – это такой денежный поток, у которого длительность всех периодов равны между собой. Аннуитет в финансовой литературе часто называют финансовой рентой или просто рентой. Любое денежное поступление называется членом ренты, а величина постоянного временного интервала между двумя последовательными денежными поступлениями называется периодом аннуитета (ренты). Если число равных временных интервалов ограничено, аннуитет называется срочным. Если в течение каждого базового периода начисления процентов на денежные поступления происходит р раз, то аннуитет называют р-срочным. Как и в общем случае оценки денежных потоков применительно к аннуитетам выделяют два типа аннуитетов: пренумерандо и постнумерандо. Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении очередного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для крупной покупки.
Пример. Рассчитать приведенную стоимость переменного аннуитета постнумерандо (тыс. грн.): 12, 15, 9, 25, если заданная процентная ставка составляет 12% и период равен одному году.
61 44,97 Пример. Вам предлагается сдать в аренду участок на три года, выбрав один из двух вариантов оплаты аренды: а) по 10 тыс. грн. в конце каждого года; б) 35 тыс. грн. в конце трехлетнего периода. Какой вариант предпочтительнее, если банк предлагает 20% годовых по вкладам?
Таким образом, расчет показывает, что вариант а) выгоднее. Нами рассмотрен наиболее общий вариант постановки задачи, когда денежные поступления имеют место один раз в конце периода и сложные проценты начисляются один раз за период. Так как логика срочных постоянных аннуитетов довольно часто встречается в финансовых контрактах, есть необходимость рассмотреть и другие возможные варианты финансовых условий, а именно: денежные поступления могут иметь место несколько раз за период, начисление процентов может проводиться не только ежегодно, но и несколько раз на год, может использоваться не только схема сложных, но и схема простых процентов и пр.
Пример. Вам предлагается сдать в аренду участок с арендной платой в размере 5 тыс. грн. в конце каждого полугодия. При этом возможно начисление процентов: а) ежегодное; б) полугодовое; в) ежеквартальное. Какой из вариантов предпочтительнее?
а) ежегодное начисление процентов. Возможно либо начисление сложных, либо простых процентов. Будущая стоимость аннуитета при начислении сложных процентов:
Если в течение года начисляются простые процента, то будущая стоимость аннуитета составит:
б) начисление процентов по полугодиям:
в) ежеквартальное начисление процентов:
Аннуитета постнумерандо. В этом случае производится оценка будущих денежных поступлений с позиции текущего момента, под которым понимается момент времени, начиная с которого отсчитываются равные временные интервалы, входящие в аннуитет. Общая формула для оценки текущей стоимости срочного аннуитета постнумерандо выводится из ранее выведенной основной формулы и имеет вид:
Множитель
Экономический смысл дисконтного множителя Дисконтный множитель Из ранее выведенной формулы для определения множителя В случае рассмотрения только сложных процентов формулы для нахождения приведенных стоимостей аннуитетов аналогичны формулам для нахождения наращенных сумм. Получающиеся при этом денежные потоки будут представлять собой геометрические прогрессии, знаменателями которых будут соответствующие дисконтные множители. Так, для постоянного аннуитета постнумерандо с начислением сложных процентов m раз за базовый период приведенный денежный поток имеет вид:
Следовательно, приведенная стоимость такого аннуитета будет равна:
Для р-срочных аннуитетов с начислением сложных процентов соответственно один раз за базовый период и m раз за базовый период аналогичным образом можем получить следующие формулы для определения приведенной стоимости:
Пример. Страховая компания, заключив на 4 года договор с некоторой фирмой, получает от нее страховые взносы по 20 тыс. грн. в конце каждого полугодия. Эти взносы компания помещает в банк под 12% годовых. Необходимо найти приведенную стоимость суммы, которую получит страховая компания по данному контракту, если проценты будут начисляться: а) раз в полгода; б) ежемесячно. а) полугодовое начисление процентов: n = 4, r = 12%, m = 2, p = 2.
б) ежемесячное начисление процентов: n = 4, r = 12%, m = 12, p = 2.
Пример. Банк предлагает ренту постнумерандо на 10 лет с ежеквартальной выплатой 100 грн. Годовая процентная ставка в течение всего периода остается постоянной. По какой цене можно приобрести такую ренту, если выплаты начнут осуществляться: а) немедленно; б) через 2 года; в) через 3,5 года, а процентная ставка равна 2, 4, 12% годовых.
а) вариант немедленного начала выплат. n = 10*4 = 40, r = 2%:4 = 0,5%.
б) вариант начала выплат через 2 года. N = 40, r = 4%: 4 = 1%, h = 2*4 = 8.
в) вариант начала выплат через 3,5 года. n = 40, r = 12%: 4 = 3%, h = 3,5 *4 = 14.
Из рассмотренного примера видно, что с ростом процентной ставки и срока, после которого начнутся выплаты, приведенная стоимость аннуитета уменьшается. Так, если выплаты начнутся через 3,5 года и процентная ставка составит 12% годовых, то указанную ренту можно приобретать за 1528,15 грн. или, естественно, дешевле. В то же время приведенная стоимость ренты с отсрочкой выплаты на 2 года и при процентной ставке 4% годовых составляет вдвое больше – 3032,23 грн. Как следует из формулы для определения будущей стоимости аннуитета постнумерандо в самом общем виде для нахождения
Если известна приведенная стоимость и остальные параметры, а необходимо найти величину разового платежа, то используется формула:
Величину разового платежа можно определить иначе. Мы помним, что
Аналогичным образом можно получить формулу для определения величины разового платежа (или поступлени
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 833; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.248.140 (0.014 с.) |


 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.


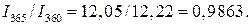


 . Тогда в формуле процентных денег
. Тогда в формуле процентных денег  можно записать
можно записать  . Поделив числитель и знаменатель дроби правой части равенства на r, получим:
. Поделив числитель и знаменатель дроби правой части равенства на r, получим: , где
, где  .
. т.н. процентное число;
т.н. процентное число; процентный ключ или дивизор.
процентный ключ или дивизор. , но при различных значениях
, но при различных значениях  (360 или 365 дней) будет разным и дивизор.
(360 или 365 дней) будет разным и дивизор. получается 1 денежная единица в день.
получается 1 денежная единица в день. грн. (при t=T), то I =
грн. (при t=T), то I =  *r = t (грн.в день).
*r = t (грн.в день). тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.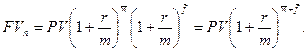

 - количество начислений в году;
- количество начислений в году; - целое число подпериодов в
- целое число подпериодов в  годах;
годах; – дробная часть подпериода.
– дробная часть подпериода. тыс. грн.
тыс. грн. тыс. грн.
тыс. грн. ;
;  ;
;  ;
; 
 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн. ;
;  ;
; 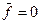 , т.е. продолжительность ссуды равна целому числу подпериодов. Поэтому обе схемы дают один и тот же результат:
, т.е. продолжительность ссуды равна целому числу подпериодов. Поэтому обе схемы дают один и тот же результат: тыс. грн.
тыс. грн. тыс. грн..
тыс. грн..  тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.  тыс. грн.
тыс. грн.

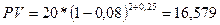 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.
 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.
 или
или 
 тыс. грн.
тыс. грн.  тыс.грн.
тыс.грн. или, если m=1
или, если m=1 
 года
года , или, если m=1
, или, если m=1 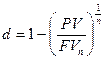
 или 13,82%.
или 13,82%. установлены сложные учетные ставки соответственно
установлены сложные учетные ставки соответственно  . Тогда при наращении сложными процентами итоговая сумма за время
. Тогда при наращении сложными процентами итоговая сумма за время 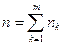 (если все периоды времени измеряются в одних единицах) определяется по формуле:
(если все периоды времени измеряются в одних единицах) определяется по формуле: .
. , тогда формула для определения наращенной суммы примет вид:
, тогда формула для определения наращенной суммы примет вид:  .
. грн.
грн.


 .
. .
. .
. ;
; .
. и поэтому
и поэтому  .
. или 12,196%.
или 12,196%. тыс. грн.
тыс. грн. . Она обеспечивает переход от к при заданных значениях этих параметров и однократном дисконтировании в течение года.
. Она обеспечивает переход от к при заданных значениях этих параметров и однократном дисконтировании в течение года. , то после соответствующих преобразований получим:
, то после соответствующих преобразований получим:  .
. .
. , и дисконтированная каким-либо образом за время
, и дисконтированная каким-либо образом за время  .
. , откуда
, откуда  .
.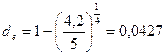
 тыс. грн.
тыс. грн.

 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн.
 называется коэффициентом дисконтирования ренты и как сумма членов геометрической прогрессии равен величине:
называется коэффициентом дисконтирования ренты и как сумма членов геометрической прогрессии равен величине:
 заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярным денежным поступлением в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя табулированы в финансовых таблицах.
заключается в следующем: он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярным денежным поступлением в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя табулированы в финансовых таблицах.



 тыс. грн.
тыс. грн. тыс. грн.
тыс. грн. грн.
грн.
 грн.
грн.
 грн.
грн.


 Значит,
Значит,  , откуда с помощью несложных преобразований, получим:
, откуда с помощью несложных преобразований, получим:



