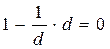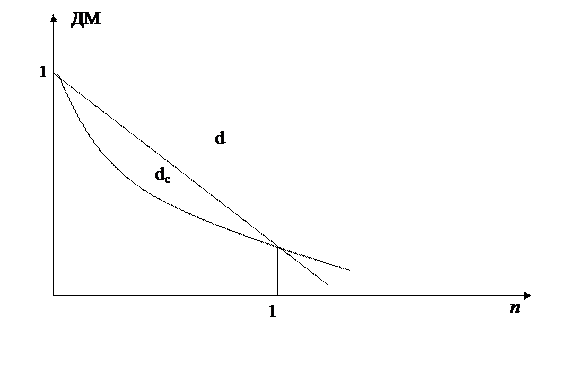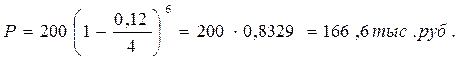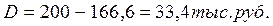Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисконтирование с использованием сложных процентовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При изучении простых процентов были рассмотрены два метода дисконтирования – математический и банковский учет. Первый заключается в определении P по значению S при заданном уровне ставки процента i, второй – при заданном уровне учетной ставки d. Для математического дисконтирования по сложным процентам решим уравнение (23) относительно P:
где называется дисконтным множителем. В случае, когда проценты начисляются m раз в год, величина P определяется как:
где j – номинальная ставка процентов; n – срок ссуды в годах. Дисконтный множитель равен
Здесь также величина P, полученная дисконтированием S, называется современной или приведенной величиной S. При начислении на величину P процентов по ставке i она принимает значение величины S через n лет. Таким образом, эти величины с учетом временного фактора эквивалентны. Разность между S и P является дисконтом, который равен: D = S – P = S – S∙vn = S (1 - vn), D = S – P = S – S∙vm·n = S (1 - vm∙n). Являясь одной из основных характеристик в финансовом анализе, современная величина требует рассмотрения ее основных свойств. Одно из этих свойств заключается в том, что чем выше ставка процентов, тем более интенсивно происходит дисконтирование и, как следствие, в большей степени уменьшается первоначальная величина P при прочих равных условиях (рис. 7).
i Рис. 7. Зависимость дисконтного множителя от величины процентной ставки Пример 24. Определим современную величину банковского депозита, если вкладчик через 10 лет должен получить 2 млн. руб. Банк производит начисление на внесенную сумму по сложной ставке – 20% годовых.
Если же начисление процентов производится ежеквартально, то первоначальная сумма вклада значительно меньше.
Большое влияние на процесс дисконтирования оказывает срок платежа. С увеличением срока платежа современная величина будет становиться все меньше. Предел значений Р при сроке платежа n, стремящейся к бесконечности:
Оказывает влияние на процесс нахождения современной величины и число раз начисления процентов m. С ростом величины m дисконтный множитель
Величина Р может быть определена на любой момент времени до момента выплаты суммы S. Чем ближе момент, для которого определяется современная величина Р, к моменту выплаты суммы S, тем меньше сумма дисконта. Пример 25. Определить величину дисконта, если заемщик должен уплатить 500 тыс. руб., срок ссуды 90 дн., ставка 130% годовых. Долговое обязательство было учтено в банке кредитором: а) за 20 дней до установленного срока, б) за 10 дней до установленного срока. а)
б)
Соотношение между дисконтным множителем, рассчитанным по простой и сложной ставке процентов, зависит от срока сделки. В случае равенства iП = iС для срока менее года имеем: (1 + ni)-1 < (1 + iC)-n Для срока более года имеем: (1 + ni)-1 > (1 + iC)-n Где: iП и iС – соответственно простые и сложные ставки. Пример 26. Учет ссуды производится через 6 месяцев после ее выдачи. Определить величину дисконтного множителя при равенстве простой и сложной процентной ставке, равной 120% годовых (iП = iС = 1,2) Определяем дисконтные множители:
по сложной ставке:
Чем больше срок ссуды, тем больше различия в величинах дисконтных множителей.
Операции со сложной учетной ставкой В учетных операциях наряду с использованием простых и сложных процентных ставок используются и сложные годовые учетные ставки. В этих случаях процесс дисконтирования происходит с замедлением, так как на каждом шаге во времени или в каждом периоде учетная ставка применяется не к первоначальной сумме, как при учете при простой учетной ставке, а к сумме, уменьшенной на величину дисконта, определенного на предыдущем шаге.
P = S (1 - d с) n, (38) где d с – сложная годовая учетная ставка; n – срок ссуды. В этом случае дисконт определяется по формуле: D = S – P = S – S (1 – d с) n = S {1 – (1 – d с) n }. (39) Величина учетной ставки определяется в зависимости от срока наступления платежа по долговому обязательству и действующей процентной ставки.
Пример 27. Владелец векселя номиналом в 200 тыс. руб. с периодом обращения 1,5 года предложил его банку для учета. Банк произвел учет векселя по сложной учетной ставке, равной 12% годовых. Определить дисконт, полученный банком и сумму, полученную владельцем векселя.
Р = 200(1 – 1,12)1,5 = 200 ∙ 0,8255 = 165,1 тыс. руб. D = 200 – 165,1 = 34,9 тыс. руб. Рассмотрим другую ситуацию. По условиям предыдущей задачи определим сумму, полученную владельцем векселя, если при учете была использована простая учетная ставка. P = S(1 - ndn) = 200(1 – 1,5 ∙ 0,12) = 200 ∙ 0,82 = 164 тыс. руб. Таким образом, дисконтирование по сложной учетной ставке для владельца векселя выгоднее, чем по простой учетной ставке. Это различие обусловлено математическими свойствами простой и сложной учетной ставки. Действительно, при использовании для дисконтирования простой учетной ставки P = S(1 - nd) значение дисконтного множителя равномерно уменьшается по мере роста величины n и достигает нуля при
P = S(1 - dc)n множитель экспоненциально уменьшается и достигает нуля лишь в пределе при n →∞ (рис. 8)
Рис. 8. Зависимость дисконтного множителя от применяемой ставки
Номинальная и эффективная процентная ставка При дисконтировании m раз в году применяют номинальную ставку f. Дисконтирование в каждом периоде будет осуществляться по ставке f/m по формуле: P = S(1 – f/m)n (40) где: N = m ∙ n, т.е. – общее число периодов дисконтирования. Пример 28. Владелец векселя номиналом в 200 тыс. руб. с периодом погашения 1,5 года предложил банку учесть его. Банк согласился на учет векселя, применив сложную учетную ставку в 12% годовых. Дисконтирование по этой ставке производится ежеквартально. По условию: f = 0,12 N = 4 ∙ 1,5 = 6.
Таким образом, дисконтирование не один, а m раз в году замедляет этот процесс и уменьшает сумму дисконта при прочих равных условиях, что для банка, как правило, невыгодно.
Под эффективной учетной ставкой понимается сложная годовая ставка, эквивалентная номинальной ставке процентов при заданном значении m. Она определяется по формуле: dэф = 1 – (1 – f/m)mn (41) Пример 29. Обязательство, равное 400 тыс. руб. должно быть погашено через 5 лет. Учетная ставка 10% годовых. Начисление дисконта поквартальное. Определить современную величину обязательства и эффективную учетную ставку. По условию: S = 400 тыс. руб. f = 0,10 n = 5 m = 4 Р = 400 (1 – 0,1/4)4∙5 = 400 ∙ 0,6027 = 271,07 тыс. руб. Определяем эффективную учетную ставку: dэф = 1 – (1 – 0,1/4)4 = 0,0963 или 9,63% Таким образом dэф < fном, эффективная учетная ставка меньше номинальной ставки.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 876; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.107.103 (0.012 с.) |

 , (36)
, (36)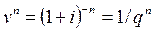
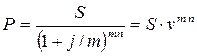 , (37)
, (37)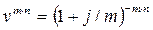 .
. v
v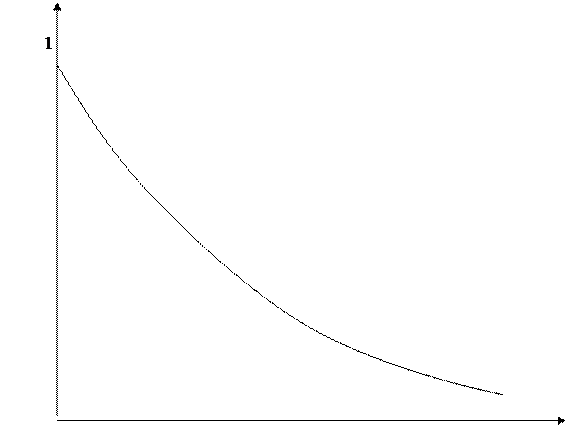
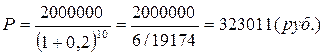
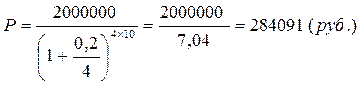
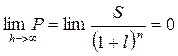
 Практически при очень больших сроках платежа его современная величина будет крайне незначительна. На практике, особенно в условиях инфляции, срок платежа регулируется приемлемыми для партнеров разумными пределами.
Практически при очень больших сроках платежа его современная величина будет крайне незначительна. На практике, особенно в условиях инфляции, срок платежа регулируется приемлемыми для партнеров разумными пределами.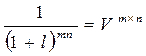 уменьшается, следовательно, уменьшается и современная величина. Эту зависимость можно увидеть в предыдущем примере.
уменьшается, следовательно, уменьшается и современная величина. Эту зависимость можно увидеть в предыдущем примере.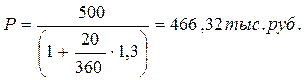
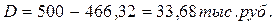

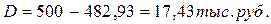
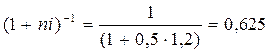

 , т.е.
, т.е.