
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наращение процентов m раз в году. Номинальная ставкаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Номинальная ставка - годовая ставка, по которой проценты начисляются m раз в году. Обозначим эту ставку через j. Если проценты начисляются m раз в году, то наращение процентов происходит по ставке Формула наращения процентов по номинальной ставке j при m-разовом начислении процентов в году примет вид:
Если j- номинальная ставка сложных процентов, то при m = 2 получается полугодовая ставка, при m = 4 - квартальная, при m = 12 - ежемесячная, при m = 365 (360) - ежедневная ставка процентов. Задача 4. Очень важная задача! Обязательная задача при зачете по сложным процентам. Вложены деньги в банк в сумме 5 млн. руб. на 2 года с полугодовым начислением процентов под 20% годовых. Составить схему наращения капитала, найти наращенные суммы по периодам начисления и к концу срока двумя способами: 1. по определению сложных процентов (как процент на процент); 2. по формуле
Решение: Рассчитаем полугодовую ставку Способ. По первому способу сумма, с которой идет наращение, увеличивается с каждым наращением процентов, т.к. по определению сложных процентов база для начисления изменяется за счет присоединения полученных на предыдущем шаге процентов, т.е.
Способ. По второму способу наращения начальный капитал К=5,0 млн. руб. остается неизменным.
Естественно, что по обоим способам результаты получились одинаковыми. Задача 6. Сумма 10 млн. руб. инвестирована на 2 года по годовой ставке 120%. Найти наращенные за это время суммы и приросты при начислениях: 1. ежегодном (m=1), 2. полугодовом (m=2), 3. ежеквартальном (m=4), 4. ежемесячном (m=12), 5. ежедневном (m=365). Решение: 1. при ежегодном начислении процентов
2. при полугодовом начислении процентов
3. при ежеквартальном начислении процентов
При ежемесячном начислении процентов
5. при ежедневном начислении процентов
Итак, чем чаще начисляются проценты, тем больше получается наращенная сумма.
Помните, что это справедливо при прочих равных условиях, А именно, ставка, срок, начальный капитал остаются неизменными, меняется только число начислений процентов в году. Непрерывные проценты
Если число начислений процентов в году m®¥, то формула наращения принимает вид
где d- непрерывная ставка, Задача 7. На сумму 10 млн руб. начислить проценты по непрерывной ставке d=12% за 5 лет. Решение:
Дисконтирование по сложным процентам
Найдя из всех формул начальный капитал К, получим уравнение дисконтирования. Полученная при дисконтировании величина К часто называется сегодняшней или современной величиной
Наращение и дисконтирование по сложной учетной ставке
Начислять проценты можно и по сложной учетной ставке:
m - число начислений процентов в году (при m=1, d = f).
Начисление процентов по ставке i называется декурсивным, а по учетной ставке d - антисипативным.
Антисипативное начисление дает большую наращенную сумму и используется в условиях высокой инфляции. Задача 8. Вексель на 10 млн. руб. со сроком платежа через 5 лет учтен: 1) по сложной учетной ставке 10% годовых; 2) по простой учетной ставке 10% годовых. Какое дисконтирование выгоднее векселедержателю? Решение: 1) по сложной учетной ставке
2) по простой учетной ставке
Итак, векселедержателю выгоднее дисконтирование по сложной учетной ставке, т.к. в день учета он получит большую сумму. Задача 9. Капитал 20 млн. руб. вложен на 4 года под 4% годовых. Найти доход от вложения денег при 1) декурсивном, 2) антисипативном способах расчета. Какое вложение выгоднее кредитору? Решение: Т.к. срок вложения денег больше 1 года, расчет сделаем по сложным процентам. Декурсивные проценты
Антисипативные проценты
Антисипативное начисление процентов выгоднее кредитору, т.к. он получает больший доход. Эквивалентные ставки (Очень важное и очень трудное понятие)
Мы рассмотрели все возможные способы начисления процентов. Однако, по какой бы ставке не начислялись проценты, следует соблюдать принцип эквивалентности, в соответствии с которым финансовый результат должен быть одинаков при начислении по любой ставке.
Такие ставки называются эквивалентными и находятся из равенства взятых попарно множителей наращения или дисконтирования.
Сравним, к примеру, множители наращения сложных процентов при начислении один раз и m раз в году:
Из равенства найдем
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.005 с.) |

 , общее число начислений процентов за срок n равно mn.
, общее число начислений процентов за срок n равно mn. .
.
 ; Множитель наращения
; Множитель наращения 
 .
.



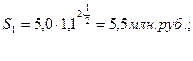





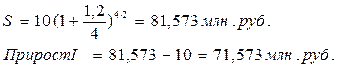



 - показатель роста.
- показатель роста.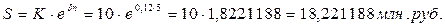
 ,
,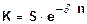 .
. или
или 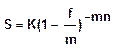 , где d и f - годовые сложные учетные ставки,
, где d и f - годовые сложные учетные ставки,

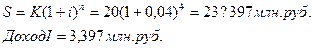
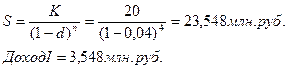
 .
. .
.


