
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первый способ: Погашение основного долга равными суммамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть долг D погашается в течение n лет,
Размер долга уменьшается, и остатки долга соответственно равны:
Т.к. проценты начисляются на непогашенный остаток долга, то они также уменьшаются. Пусть проценты выплачиваются один раз в году по ставке g. Процентные платежи по годам соответственно равны:
Сумма выплаченных процентов:
Общая сумма погашения кредита:
Если взносы в погашение кредита будут осуществляться р раз в году, то общая сумма выплаченных процентов
Пример 2.
Долг 1000 тыс. руб. необходимо погасить последовательными равными суммами за 5 лет платежами постнумерандо. За заем выплачиваются проценты по годовой ставке 10%. Составить план погашения кредита.
Решение: Итак, долг D = 1 000 тыс. руб., ежегодная выплата долга Выплаченные проценты за 1-й год J1 = 1 000 ´ 0,1 = 100 тыс. руб.; Выплаченные проценты за 2-й год J2 = (1 000 – 200) ´ 0,1 = 80 тыс. руб. и т.д.
Расчеты по погашению долга приведены в таблице 1. Таблица 1
Расход по займу равен сумме расходов по погашению основного долга и расходов по выплаченным процентам, т.е. Y = R +I. Основной недостаток такого расчета погашения долга – большие платежи в начале выплат.
Второй способ: погашение долга равными срочными выплатами
По этому способу расходы должника по обслуживанию долга постоянны на протяжение всего срока его погашения.
Из общей суммы расходов должника часть выделяется на уплату процентов, остаток идет на погашение основного долга. Периодическая выплата постоянной суммы Y = R равнозначна ренте с заданными параметрами. Ее современная стоимость A = сумме долга D, т.е.
Обозначим через Тогда расход по займу
Пример 3.
Долг 1 000 тыс. руб. погашается в течение 5 лет платежами постнумерандо по ставке g = 10%. Составить план погашения кредита равными срочными выплатами с начислением процентов на непогашенный остаток. Решение: Рассчитаем расход по займу R = Y.
Первая выплата основного долга d1 = 263,787 – 1 000 ´ 0,1 = 163,787 тыс. руб.; остаток долга D1 = 1 000 – 163,787 = 836,203 тыс. руб.; Вторая выплата основного долга d2 = 263,783 – 836,203´0,1 = 180, 177 тыс. руб. и т. д.
Расчеты по погашению долга приведены в таблице 2. Таблица 2
При таком погашении долга процентные платежи уменьшаются во времени, а сумма погашения основного долга увеличивается, расходы по займу остаются постоянными на весь срок, однако в этом случае должник немного переплачивает.
Погашение потребительского кредита
В потребительском кредите проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент открытия кредита, т.е разовым начислением процентов. Величина разового погасительного платежа
n – срок кредита в годах, p – число платежей в году.
Для решения проблемы определения остатка задолженности на любой момент времени следует разбить величину Y на проценты и сумму, идущую на погашение основного долга.
Рассмотрим возможность такового разбиения двумя способами
Первый способ: равномерное распределение выплаты процентов Величину разового платежа Y представим в виде суммы
D – цена товара (сумма основного долга без процентов); R – размер погашения основного долга; I – процентный платеж.
Замечание: В случае срока кредита больше года применяются сложные проценты. Тогда процентный платеж I=D((1+g)n-1).
Второй способ: правило 78 Сумма порядковых номеров месяцев в году равна 78, отсюда и название правила. Допустим, что срок кредита равен 1 год. Тогда согласно правилу 78 доля процентов в сумме расходов в первом месяце равна 12/78, во втором она составит 11/78 и т.д. Последняя уплата процентов равна 1/78. Таким образом, доля процентов убывает, сумма погашения основного долга увеличивается. Для годового срока:
Пример: Потребительский кредит размером 240 тыс. руб., предоставленный на 1 год по ставке 20% годовых погасить по правилу 78.
Решение: Общая сумма задолженности S = 240(1+0.2) = 288 тыс. руб. Общая сумма выплаченных процентов I = 48 тыс. руб. Сумма расходов по обслуживанию долга (ежемесячная выплата) Y = 288/12 = 24 тыс. руб. Находим процентные платежи по месяцам. Для первого месяца:
Для второго месяца:
Для двенадцатого месяца:
Обобщим правило 78 для кредита со сроком N месяцев.
Последовательные номера месяцев в обратном порядке представляют собой числа: t = N, N-1,..., 1. Сумма этих чисел находится по формуле суммы арифметической прогрессии:
Ежемесячные выплаты процентов
Сумма списания основного долга
В каждом месяце выплаты процентов сокращаются на величину
Важно отметить, что в потребительском кредите при разовом начислении процентов должник фактически выплачивает проценты и за описанные суммы долга, т.е. кредит обошелся бы дешевле, если бы проценты начислялись на остатки долга.
Потребительский кредит в сумме 10 млн. руб. выдан на три года при разовом начислении процентов по ставке 10% годовых. Погашение задолженности помесячное. Составить амортизационные планы погашения кредита a) по правилу 78; б) по методу равномерного распределения выплат процентов.
Решение:
А) по правилу 78:
Общая сумма долга
Сумма расходов по обслуживанию долга
Сумма последовательных номеров месяцев
Рассчитаем процентные платежи I и суммы погашения основного долга R: Для 1-го месяца
Для 2-го месяца
Для 30-го месяца
Для 36-го месяца
Общая сумма процентных платежей
Общая сумма выплат основного долга
б) по методу равномерного распределения выплат процентов:
Величину разового платежа Y представим в виде суммы
Ежемесячная выплата основного долга
Ежемесячная выплата процентного платежа
Модуль 7. Ценные бумаги Облигации
Облигации – ценные бумаги с фиксированным доходом. Они могут выпускаться в обращение государством, региональными властями, финансовыми институтами, а также различными корпорациями. Облигация – ценная бумага, подтверждающая обязательство эмитента возместить владельцу её номинальную стоимость в оговоренный срок и выплатить причитающийся доход.
По способам выплат дохода различают облигации: - с фиксированной купонной ставкой; - с плавающей купонной ставкой; - с равномерно возрастающей купонной ставкой; - с нулевым купоном (эмиссионный курс облигации ниже номинального, разница выплачивается в момент погашения облигаций, процент не выплачивается); - смешанного типа. По способам обеспечения: - с имущественным залогом; - с залогом в форме будущих залоговых поступлений; - с определенными гарантийными обязательствами; - необеспеченные (беззакладные). По характеру обращения: - конвертируемые; - обычные. По сроку действия: - краткосрочные (1-3 года); - среднесрочные (3-7 лет); - долгосрочные (7-30 лет); - бессрочные.
К основным параметрам облигаций относятся: номинальная цена; выкупная цена в случае, если она отличается от номинальной; норма доходности и сроки выплаты процентов. Периодическая выплата процентов по облигациям осуществляется по купонам 1 раз в год, 1 раз в полугодие, 1 раз в квартал, в неопределенное заранее время.
Виды цен облигаций 1) Нарицательная или номинальная цена N:
2) Эмиссионная цена Р или цена первичного размещения долговых обязательств. Если Р < N, цена называется дисконтной или со скидкой. Если Р > N, цена называется с премией (ажио).
3) Рыночная или курсовая цена Рыночные цены существенно различаются между собой, поэтому для достижения их сопоставимости рассчитывается курс облигации.
Под курсом облигации понимают покупную цену одной облигации в расчете на 100 денежных единиц номинала, т.е.
4) Выкупная цена или цена по истечению срока займа S.
Пример1: Определить курс облигации номиналом N=1000 руб., если она реализована на рынке по цене а) 920,30 руб.; б) 1125,0 руб. Решение: а) Курс облигации
б) Курс облигации
В случае а) облигация приобретена с дисконтом 1000 - 920,30 = 79,70 руб.; в случае б) – с премией 1000 – 1125 = -125 руб., означающей снижение общей доходности операций для инвестора. Пример 2. Облигации номиналом N=25 тыс. руб. продаются по цене 24,5 тыс. руб. Найти курс облигаций. Решение: Курс облигации
Облигация куплена с дисконтом.
Пример 3. Курс ГКО (государственные краткосрочные облигации) номиналом N=100 тыс. руб. равен 77,5. Найти текущую цену облигации. Решение: Текущая цена облигации равна
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 5953; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.008 с.) |






 .
. = 200 тыс. руб.
= 200 тыс. руб.
 - коэффициент приведения годовой ренты со ставкой процентов g и сроком n.
- коэффициент приведения годовой ренты со ставкой процентов g и сроком n.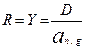 , а сумма первого взноса по погашению основного долга d1 = Y – Dg.
, а сумма первого взноса по погашению основного долга d1 = Y – Dg.
 , где
, где , где
, где



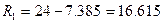 тыс. руб.
тыс. руб.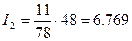
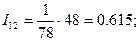
 тыс. руб.
тыс. руб. .
.
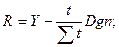
 , на такую же величину увеличивается сумма списания основного долга.
, на такую же величину увеличивается сумма списания основного долга. руб.
руб.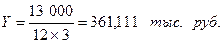

 ;
; ;
; ;
;




 .
.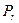 .
. .
.







