
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекции по финансовой математикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лекции по финансовой математике
Модуль 1. Простые проценты
Золотое правило бизнеса: Сумма, полученная сегодня, больше той же суммы, полученной завтра В основе финансово-экономических расчетов лежит понятие временной ценности денег. В практических финансовых и коммерческих операциях суммы денег обязательно связываются с некоторыми конкретными моментами или интервалами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность поступлений денежных средств или их выплат. Фактор времени играет не менее важную роль, чем размеры денежных сумм. Необходимость учета фактора времени определяется принципом не равноценности денег, относящихся к разным периодам времени. Дело в том, что, даже в условиях отсутствия инфляции и риска, 1000 руб., полученных через год, не равноценны этой же сумме, полученной сегодня. Не равноценность определяется тем, что любая сумма денег может быть инвестирована сегодня и принести доход в будущем. Поступившие доходы в свою очередь могут быть реинвестированы и т.д. Следовательно, сегодняшние деньги в этом смысле ценнее будущих, а будущие поступления менее ценны, чем современные. Известный афоризм, «время - деньги» (Time is money) как нельзя лучше выражает сущность современного количественного финансового анализа.
Расчет и анализ любой финансовой операции начинается с приведения всех платежей, осуществленных в различные моменты времени, к одному моменту (настоящему или будущему), только после этого денежные суммы можно между собой сравнивать, вычитать, складывать.
Описание изменения денежных сумм во времени производится путем вычисления дохода от инвестирования денег, т.е. путем начисления процента на первоначальную сумму, поэтому теория процентных ставок – основа временной стоимости денег.
Основные понятия кредитной операции
Получение кредита – наиболее распространенная финансовая сделка. Она характеризуется следующими величинами:
K – начальный капитал или сумма ссуды;
S – наращенная сумма или полная стоимость кредита с процентами.
I = S - K – доход (процентные деньги, проценты), получаемый кредитором от предоставления денег в долг;
n – период начисления процентов в годах,
Процентная ставка i может измеряться в процентах (%), в виде десятичной или натуральной дроби.
Например: i=15% =0.15; i=200%=2.0 и т.д.
В формулах для финансовых расчетов процентная ставка берется в виде десятичной дроби.
1. По базе начисления проценты делятся на простые и сложные. Если база постоянна на весь период начисления процентов, используют простые проценты. Обычно период начисления в этом случае n < 1 года. Если за базу для начисления принимается сумма, полученная из предыдущей, с прибавлением к ней процентов,то используют сложные проценты (иначе, процент на процент)
2. По принципу расчета процентов различают ставки наращения i и учетные ставки d. Плата за кредит может взиматься как в конце срока, так и в его начале. В первом случае проценты начисляются в конце срока, исходя из величины предоставляемой суммы K, и возврату подлежит сумма долга вместе с процентами, т.е S = K + I. Такой способ начисления процентов называется декурсивным.
Во втором случае процентный доход D называемый дисконтом, выплачивается в начале срока. При этом должнику выдается сумма, уменьшенная на его величину, т.е S - D; а возврату в конце срока подлежит вся исходная ссуда S. Такой способ начисления процентов называется антисипативным, а процентная ставка – учетной ставкой. Учетная ставка
3. Процентные ставки могут быть фиксированными (постоянными), когда в контракте (сделке, финансовой операции) указывается их размер или «плавающие», когда фиксируется не сама ставка, а изменяющиеся во времени базовая ставка и надбавка к ней, называемая маржой.
4. По периоду начисления проценты делятся на дискретные проценты и непрерывные проценты. Дискретные проценты начисляются за фиксированные в договоре интервалы времени (год, полгода, квартал, месяц, день). Непрерывные проценты связаны с непрерывным интервалом начисления.
Операция наращения состоит в том, что по сегодняшней сумме ссуды K рассчитывается ее будущая стоимость S. Операция дисконтирования состоит в том, что на сегодняшний момент времени пересчитывается некоторая будущая сумма денег S. В этом случае сумму K называют современной или приведенной величиной. Простые проценты
Простые проценты - это метод расчета дохода кредитора от предоставления денег в долг заемщику. Сущность простых процентов состоит в том, что они начисляются на одну и ту же величину капитала К в течение всего срока ссуды. Простые проценты дают больший доход при их начислении на срок меньше года. Основная формула простых процентов:
К - начальный капитал, I - доход (процентный платеж, процентные деньги или просто проценты), получаемый кредитором от заемщика за пользование денежной ссудой; p - процентная ставка, показывающая сколько денежных единиц должен заплатить заемщик за пользование 100 ед. капитала за год, т. е. годовая ставка в процентах. Если ставка измеряется в долях единицы, то она обозначается буквой
Если деньги отданы взаймы под проценты, то заемщик возвращает наращенную сумму
S = K + I = K + Kni = K(1 + ni), где
Доход за n лет I = Kni, (1 + ni) - множитель наращения по простым процентам.
Итак, если по начальному капиталу (сегодняшним деньгам) K находится будущая сумма денег S, то операция называется наращением. Если же, зная будущие деньги S, находят их сегодняшнюю сумму K по формуле:
Задача1. Капитал 200 тыс.руб. вложен в банк на 8 месяцев под 12% годовых. Найти сумму, которая будет получена к концу срока. К = 200 тыс.руб., n =
Решение: I способ. S = K + I, I = I =
S = 200 + 16 = 216 тысяч руб. II способ. Ставка годовая, срок n в месяцах переведем в доли года: n = 8 месяцев = S = K(1 + ni)=200(1 + Задача 2. Капитал 200 тыс.руб. вложен в банк на 80 дней под 12% годовых. Найти величину вклада через 80 дней. Расчет сделать точным и банковским методом. Решение: K = 200 тысяч руб. n = 1.Точный метод: Т.К. ставка годовая, срок n переведем в доли го да: n = S = K(1 + ni) = 200(1 + 1. Банковский метод: Срок n =
Задача 5. Платежное обязательство уплатить через 100 дней 2 млн. руб. с процентами, начисляемыми по ставке простых процентов i=20% годовых, было учтено за 40 дней до срока погашения по учетной ставке d =15%. Требуется найти сумму, полученную при учете.
Решение:
Задача 7. Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней. Решение:
Простые переменные ставки
В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки. Если i1, i2,… ik – последовательные во времени простые ставки, а n1, n2,… nk – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:
Задача 8 Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года. Дано: n1=1 год, i1 =16%, n2=1/2 года, i2 =(16+1)% = 17%, n3=1/2 года, i3 =(17+1)% = 18%, n4=1/2 года, i4 =(18+1)% = 19%, Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года. Множитель наращения = Иначе, за 2б5 года начальный капитал увеличился в 1,43 раза.
Реинвестирование
В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!) В этом случае наращенная сумма для всего срока составит:
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:
Задача 9. Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам. Решение: По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам. По точным процентам:
(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!) По банковским процентам при условии, что в каждом месяце по 30 дней:
Модуль 2. Сложные проценты
Наращение по сложным процентам
В средне и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты. Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов. Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид
Задача 1. Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты. Решение: 1.Сложные проценты:
2. Простые проценты:
За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам. Задача 2. Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты. Решение: 1.Сложные проценты:
2. Простые проценты:
Итак, сложные проценты работают лучше, если срок n больше 1 года и простые проценты лучше работают (дают большее наращение) внутри года. Если срок начисления процентов 1 год, простые и сложные проценты дают одинаковый результат. Задача 3. Найти сумму долга в 15 млн. руб. через 8 месяцев, 320 дней, 2 года, 10 лет по сложным годовым ставкам 5% и 8%. Решение:
Сумма долга зависит от процентной ставки и числа лет начисления. Сравните суммы по годам и по процентным ставкам. (Сумма долга растет с увеличением и процентной ставки, и числа лет начисления).
Способ. По первому способу сумма, с которой идет наращение, увеличивается с каждым наращением процентов, т.к. по определению сложных процентов база для начисления изменяется за счет присоединения полученных на предыдущем шаге процентов, т.е.
Способ. По второму способу наращения начальный капитал К=5,0 млн. руб. остается неизменным.
Задача 6. Сумма 10 млн. руб. инвестирована на 2 года по годовой ставке 120%. Найти наращенные за это время суммы и приросты при начислениях: 1. ежегодном (m=1), 2. полугодовом (m=2), 3. ежеквартальном (m=4), 4. ежемесячном (m=12), 5. ежедневном (m=365). Решение: 1. при ежегодном начислении процентов
2. при полугодовом начислении процентов
3. при ежеквартальном начислении процентов
Непрерывные проценты
Если число начислений процентов в году m®¥, то формула наращения принимает вид
где d- непрерывная ставка, Задача 7. На сумму 10 млн руб. начислить проценты по непрерывной ставке d=12% за 5 лет. Решение:
Дисконтирование по сложным процентам
Найдя из всех формул начальный капитал К, получим уравнение дисконтирования. Полученная при дисконтировании величина К часто называется сегодняшней или современной величиной
Задача 8. Вексель на 10 млн. руб. со сроком платежа через 5 лет учтен: 1) по сложной учетной ставке 10% годовых; 2) по простой учетной ставке 10% годовых. Какое дисконтирование выгоднее векселедержателю? Решение: 1) по сложной учетной ставке
2) по простой учетной ставке
Итак, векселедержателю выгоднее дисконтирование по сложной учетной ставке, т.к. в день учета он получит большую сумму. Задача 9. Капитал 20 млн. руб. вложен на 4 года под 4% годовых. Найти доход от вложения денег при 1) декурсивном, 2) антисипативном способах расчета. Какое вложение выгоднее кредитору? Решение: Т.к. срок вложения денег больше 1 года, расчет сделаем по сложным процентам. Декурсивные проценты
Антисипативные проценты
Эквивалентные ставки (Очень важное и очень трудное понятие)
Мы рассмотрели все возможные способы начисления процентов. Однако, по какой бы ставке не начислялись проценты, следует соблюдать принцип эквивалентности, в соответствии с которым финансовый результат должен быть одинаков при начислении по любой ставке.
Такие ставки называются эквивалентными и находятся из равенства взятых попарно множителей наращения или дисконтирования.
Сравним, к примеру, множители наращения сложных процентов при начислении один раз и m раз в году:
Из равенства найдем
Задача 12. Годовая ставка сложных процентов равна 15%. Чему равна эквивалентная сила роста? Решение: Воспользуемся уравнением эквивалентности сложной и непрерывной ставок:
Непрерывная ставка d=13,976% и сложная ставка I=15% дают одинаковый финансовый результат. Например, при начальном капитале K=2000 руб., сроке n=4 года, имеем
Инфляция Инфляция – это обесценивание денег. В экономике различают более 20 видов инфляции: инфляция, связанная с эмиссией денег; с большими кредитными расходами; превышения спроса над предложением; с ожиданием роста цен; с изменение цен на сырье; с ростом заработной платы и т.д. Различают скрытую и открытую инфляции. Скрытой инфляции присущи дефицит товаров, отложенный спрос и постоянные цены. При открытой инфляции освобождаются цены и растут доходы. Освобождение цен при накопившихся излишках денег ускоряет обращение денег в десятки раз в связи с боязнью населения нового витка повышения цен, что приводит к гиперинфляции. Дефляция – сдерживание обесценивания денег или мероприятия по ограничению денежной массы в обращении. Осуществляется путем увеличения налогов, повышения процентных ставок, ограничения кредитов, снижения роста заработной платы, ограничения продажи ценных государственных бумаг на открытом рынке.
Характеристики инфляции 1. Индекс цен Ip или индекс покупательной способности
Индекс цен показывает, во сколько раз приросли цены за соответствующий период. Индекс покупательной способности показывает, во сколько раз уменьшилась покупательная способность за этот же период. Например, пусть сегодня получены 5000 руб. Известно, что за три предшествующих года цены возросли в 5 раз, т.е. С = 5000×
2. Темп инфляции Н - относительный прирост цен за период. Измеряется в %, находится по формуле: Следовательно, Например, если цены увеличились в 2 раза, то их прирост составил И наоборот, если темп прироста цен составил 70%, то цены увеличились в 3. Среднегодовой темп роста цен Если рассматривается индекс цен за несколько периодов, то
Если Задача 9. Темп инфляции h=10% в месяц. Найти рост цен за год и годовой темп инфляции. Решение:
Задача 10. Последовательный прирост цен за 3 месяца составил 25%, 20%, 18%. Найти темп инфляции за эти месяцы. Решение:
Два случая учета инфляции Первый случай учета инфляции: при расчете наращенной суммы. Пусть S - наращенная сумма, С - та же сумма с учетом инфляции. Конкретизируем формулу:
Для простых процентов: Наращенная сумма простых процентов Тогда
Для сложных процентов: Наращенная сумма сложных процентов
Если i > если i < если i =
Задача 11. Последовательный прирост цен за 3 месяца составил 25%, 20%, 18%. Найти реальную сумму 1,5 млн. руб., накопленные проценты и инфляционную сумму, реальный доход, реальную доходность, если наращение идет по ставке i=50% а) сложных годовых, б) простых процентов. Решение: Индекс инфляции найден в задаче 10. Цены за 3 месяца увеличились в 1,77 раз. Рассчитаем реальную сумму 1,5 млн. руб.
А) по сложным процентам: Наращенная сумма по сложным процентам
Накопленные проценты I = S – K = 1,66 – 1,5 = 0,16 млн. руб.;
инфляционная сумма (сумма, которую “съела” инфляция) Kh = S – C = 1,66 – 0,938 = 0,722 млн. руб.;
реальный доход I1 = C – K = 0,938 – 1,5 = - 0,562 млн. руб.;
реальная доходность
Сложная годовая ставка 50% при трехмесячной инфляции 77% дает отрицательную годовую доходность 150%.
б) По простым процентам: Наращенная сумма по простым процентам
Накопленные проценты инфляционная сумма
реальный доход I1 = C – K = 0,953 – 1,5 = – 0,547 млн. руб.; реальная доходность
Простая годовая ставка 50% при трехмесячной инфляции 77% дает годовую отрицательную доходность 146%. Второй случай учета инфляции: при измерении эффективности (доходности) финансовойоперации
В этом случае применяется индексация процентной ставки, которая сводится к увеличению ставки процентов на величину, так называемой, инфляционной премии.
Назовем ставку с поправкой на инфляцию брутто-ставкой и обозначим ее r (ставка i + маржа). Для нахождения брутто-ставки составляется уравнение эквивалентности множителей наращения по брутто-ставке и по ставке i с учетом инфляции. Рассчитаем брутто-ставки:
1. Для простых процентов: Уравнение эквивалентности имеет вид: реальная ставка
2. Для сложных процентов: Уравнение эквивалентности имеет вид: реальная ставка Задача 12. Продолжим решать задачу 11. В условиях этой задачи рассчитаем брутто-ставки для годовой простой и сложной ставки 50%. а) Брутто - ставка простых процентов
Простая годовая ставка 396,5% годовых компенсирует инфляцию и дает реальный доход 50% годовых. Проверка: 1) Наращенная сумма денег с учетом инфляции по брутто-ставке:
2) Наращенная сумма по ставке i без учета инфляции:
б) Брутто-ставка сложных процентов
Т.к. ставка i – годовая ставка, то темп инфляции должен быть рассчитан за год.
Годовая сложная брутто-ставка r= 1372,25% компенсирует инфляцию и дает годовой доход 50%. Проверка: 1) Наращенная сумма денег с учетом инфляции по брутто-ставке r:
2) Наращенная сумма по ставке i без учета инфляции:
Модуль 3. Консолидация и пролонгация финансовых обязательств Случай 1. Консолидированный платеж S0 расположен между консолидируемыми платежами. Иначе, есть платежи до и после консолидированного платежа. Расположим платежи на временной оси в порядке возрастания их дат.
Найдем величину консолидированного платежа S0, используя простую процентную ставку i. Платежи S1, S2, Sj производятся раньше консолидированного платежа s0, поэтому они наращиваются. Платежи Sк-1, Sк производятся позднее консолидированного платежа s0, поэтому они дисконтируются. Формула для расчета консолидированного платежа будет выглядеть так:
Случай 2.
Консолидированный платеж S0 расположен раньше всех консолидируемых платежей.
Формула для расчета консолидированного платежа будет выглядеть так:
Случай 3.
Консолидированный платеж S0 расположен позднее всех консолидируемых платежей.
Формула для расчета консолидированного платежа будет выглядеть так:
Задача 4. Три платежа Решение: Платежи и даты их выплат изобразим точками на временной оси в порядке возрастания дней выплат:
За базовую дату примем день выплаты консолидированного платежа Т.к. срок объединяемых платежей меньше срока платежа
Решение
Возьмем за базовую дату 1.04.01 и составим уравнение эквивалентности, учитывая два условия:
1) все платежи приведены к базовой дате; 2) старые долги равны новым долгам.
Т.к. базовая дата самая поздняя из всех, то платежи
Модуль 4. Рентные платежи Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени. Например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. Такие последовательности называются потоком платежей, а отдельный элемент последовательности - членом потока. Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называется финансовой рентой или аннуитетом.
Характеристики ренты
Рента характеризуется следующими параметрами: член ренты R - размер отдельного годового платежа; период ренты - временной интервал между двумя последовательными платежами; срок ренты n - время от начала первого периода ренты до конца последнего периода; процентная ставка i; число p платежей в году; частота m начисления процентов. Классификация рент
1. ренты немедленные (начало срока ренты и начало действия контракта совпадают) и ренты отсроченные; 2. ренты с ежегодным начислением процентов (m=1), начислением процентов m раз в году и непрерывным начислением процентов; 3. ренты с постоянными и переменными членами; 4. ренты конечные и бесконечные. Если срок ренты более 50 лет, рента считается вечной. 5. рента обычная или постнумерандо, если платежи производятся в конце периода; рента пренумерандо, если платежи производятся в начале периода. Пример 4-х летней ренты постнумерандо:
Пример 4-х летней ренты пренумерандо:
Обычно анализ потока платежей предполагает расчет или наращенной суммы или современной стоимости. Наращенная сумма S ренты Наращенная сумма - сумма всех членов потока платежей с начисленными на них к концу срока процентами. 1. Годовая рента постнумерандо Ее характеристики: член ренты R, срок ренты n, ставка i, число выплат в году p=1, число начислений процентов в году m=1. Положим n=4 года и выведем формулу наращенной суммы ренты. Построим схему наращения членов ренты на временной оси. Т.к. срок ренты больше одного года, естественно использовать сложные проценты. Например, на член ренты R, внесенный в конце первого года, будут начисляться проценты 3 года. К концу срока ренты эта сумма будет составлять Подобным образом, на член ренты R, внесенный в конце второго года, будут начисляться проценты 2 года. К концу срока ренты эта сумма будет составлять
Пример 1. Создается фонд. Средства в фонд поступают в виде годовой постоянной ренты в течении 6 лет в конце года. Размер разового годового платежа 20 тыс. руб. На поступившие взносы начисляются 25% годовых. Найти величину фонда к концу срока.
Решение: Рассматривается годовая рента постнумерандо, член ренты R=20 тыс. руб., срок ренты n=6 лет, ставка i=25%. Величина фонда к концу срока 2. Годовая рента, постнумерандо, начисление процентов m раз в году, выплаты p один раз в году (Характеристики ренты R, n, j, m¹1, p=1) Наращенная сумма ренты Пример 2. В условиях примера 1 найти величину фонда к концу срока, если проценты начисляются ежеквартально, т.е. m=4. Решение:
Внимание! Наращенная стоимость возрасла. Следовательно, чем чаще начисляются проценты, тем больше S. 3. Рента p-срочная постнумерандо, проценты нач |
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.134.161 (0.018 с.) |

 , n =1 год – процентная ставка – относительная величина дохода в сумме долга за единицу времени.
, n =1 год – процентная ставка – относительная величина дохода в сумме долга за единицу времени. Процентная ставка
Процентная ставка 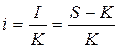 , (n=1 год) называется ставкой наращения.
, (n=1 год) называется ставкой наращения.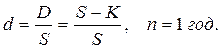

 или
или  , где
, где
 - процентная ставка в долях единицы, n- время в долях года.
- процентная ставка в долях единицы, n- время в долях года. , то операция называется математическим дисконтированием,
, то операция называется математическим дисконтированием,  - дисконтный множитель.
- дисконтный множитель. года, i = 0,12, p = 12%. S =?
года, i = 0,12, p = 12%. S =? .
. = 16 тысяч руб.
= 16 тысяч руб. года или n =
года или n =  года, i = 0,12, S=?
года, i = 0,12, S=? тыс.руб.
тыс.руб. тыс.руб.
тыс.руб.
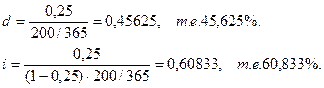


 k – количество реинвестиций.
k – количество реинвестиций. , k – количество реинвестиций.
, k – количество реинвестиций.

 , где i - годовая (номинальная) процентная ставка, n - число лет начисления,
, где i - годовая (номинальная) процентная ставка, n - число лет начисления, - множитель наращения по сложным процентам.
- множитель наращения по сложным процентам.
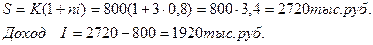
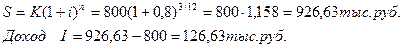

 .
.
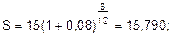

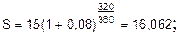
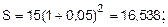

 ;
;  .
. .
.



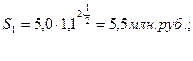





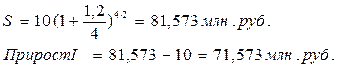

 - показатель роста.
- показатель роста.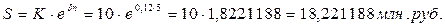
 ,
,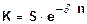 .
.

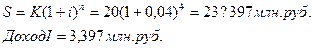
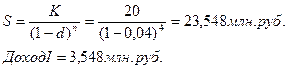
 .
. .
. Найдем из этого уравнения непрерывную ставку.
Найдем из этого уравнения непрерывную ставку.
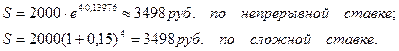
 .
.
 , тогда
, тогда  и реальная стоимость С сегодняшних денег в деньгах трехлетней давности
и реальная стоимость С сегодняшних денег в деньгах трехлетней давности = 1000 руб.
= 1000 руб. 
 .
. .
.

 , среднегодовой темп инфляции
, среднегодовой темп инфляции  .
. .
.
 , то
, то  .
.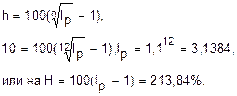 т.е. цены выросли за год в 3,1384 раза
т.е. цены выросли за год в 3,1384 раза
 .
. .
. .
. . Тогда
. Тогда .
. - реальный рост суммы денег;
- реальный рост суммы денег; млн. руб.
млн. руб. млн. руб. - реальная стоимость 1,66 млн. руб. с учетом инфляции
млн. руб. - реальная стоимость 1,66 млн. руб. с учетом инфляции
 млн. руб.
млн. руб.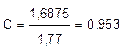 млн. руб. - реальная стоимость 1,6875 млн. руб. с учетом инфляции по простым процентам.
млн. руб. - реальная стоимость 1,6875 млн. руб. с учетом инфляции по простым процентам. млн. руб.;
млн. руб.; млн. руб.;
млн. руб.;


 ,
,

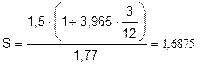 млн. руб.
млн. руб. млн. руб.
млн. руб.

 - на столько процентов увеличились цены за год.
- на столько процентов увеличились цены за год.
 млн.руб.
млн.руб.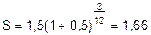 млн. руб.
млн. руб.
 .
.
 .
.
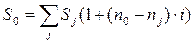 .
.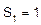 млн. руб.,
млн. руб.,  млн. руб.,
млн. руб.,  млн руб. со сроками уплаты соответственно через 100, 120 и 150 дней заменяются одним со сроком уплаты через 180 дней при простой ставке 20%. Найти сумму консолидированного платежа (год принять равным 360 дней).
млн руб. со сроками уплаты соответственно через 100, 120 и 150 дней заменяются одним со сроком уплаты через 180 дней при простой ставке 20%. Найти сумму консолидированного платежа (год принять равным 360 дней).
 .
. , то приведение платежей к моменту выплаты консолидированного платежа
, то приведение платежей к моменту выплаты консолидированного платежа 


 и
и  наращиваются.
наращиваются.
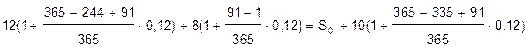
 млн. руб.
млн. руб.


 .
. . И т. д.
. И т. д.







