
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При известных суммах выплат всех платежейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этом случае все платежи приводятся на одну более раннюю дату операцией дисконтирования. Составляется уравнение эквивалентности, в левой части которого стоит дисконтированная стоимость платежа S 0, а в правой – сумма дисконтированных стоимостей объединяемых платежей P0.
Решаем задачу, используя ставку i. Запишем уравнение эквивалентности, дисконтируя все платежи, включая S0 на начальную дату «0».
Обозначим через P0 сумму дисконтированных стоимостей объединяемых платежей, т.е. Тогда
Очевидно, что в полученной формуле консолидированная стоимость платежей S0 должна быть больше суммы дисконтированных консолидируемых платежей P0. Иначе срок платежа n0 получится отрицательным. Задача 6. Фирма, в погашение задолженности банку за предоставленный кредит под 70% годовых, должна произвести 2 платежа в сроки 18.05 (138-й день), 1.09 (244-й день) суммами Найти срок выплаты консолидированного платежа. (В скобках указан порядковый номер даты платежа) Решение: Срок выплаты консолидированного платежа найдем по формуле
t = 365 дней × 0,7937»287 дней. По календарю это 14 октября (приложение табл.1).
Общая постановка задачи изменения условий выплаты платежей
При решении задачи изменения условий выплаты платежей составляется уравнение консолидации по следующему правилу: «Старые» долги равны «новым» долгам, но и те, и другие должны быть приведены на одну дату консолидации. Дата консолидации либо устанавливается во взаимном соглашении, либо выбирается произвольно. Задача 7. Две суммы 12 и 8 млн. руб. должны быть выплачены 1.09.00 (244) и 1.01.01 (1). Стороны договорились пересмотреть условия контракта: должник 1.12.00 (335) выплачивает 10 млн. руб., остаток долга гасится 1.04.01 (91). Найти эту сумму при условии, что пересчет осуществляется по ставке простых процентов, равной 12% (год равен 365 дней). Решение
Возьмем за базовую дату 1.04.01 и составим уравнение эквивалентности, учитывая два условия:
1) все платежи приведены к базовой дате; 2) старые долги равны новым долгам.
Т.к. базовая дата самая поздняя из всех, то платежи
Модуль 4. Рентные платежи Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени. Например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. Такие последовательности называются потоком платежей, а отдельный элемент последовательности - членом потока. Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называется финансовой рентой или аннуитетом.
Характеристики ренты
Рента характеризуется следующими параметрами: член ренты R - размер отдельного годового платежа; период ренты - временной интервал между двумя последовательными платежами; срок ренты n - время от начала первого периода ренты до конца последнего периода; процентная ставка i; число p платежей в году; частота m начисления процентов. Классификация рент
1. ренты немедленные (начало срока ренты и начало действия контракта совпадают) и ренты отсроченные; 2. ренты с ежегодным начислением процентов (m=1), начислением процентов m раз в году и непрерывным начислением процентов; 3. ренты с постоянными и переменными членами; 4. ренты конечные и бесконечные. Если срок ренты более 50 лет, рента считается вечной. 5. рента обычная или постнумерандо, если платежи производятся в конце периода; рента пренумерандо, если платежи производятся в начале периода. Пример 4-х летней ренты постнумерандо:
Пример 4-х летней ренты пренумерандо:
Обычно анализ потока платежей предполагает расчет или наращенной суммы или современной стоимости. Наращенная сумма S ренты Наращенная сумма - сумма всех членов потока платежей с начисленными на них к концу срока процентами. 1. Годовая рента постнумерандо Ее характеристики: член ренты R, срок ренты n, ставка i, число выплат в году p=1, число начислений процентов в году m=1. Положим n=4 года и выведем формулу наращенной суммы ренты. Построим схему наращения членов ренты на временной оси. Т.к. срок ренты больше одного года, естественно использовать сложные проценты. Например, на член ренты R, внесенный в конце первого года, будут начисляться проценты 3 года. К концу срока ренты эта сумма будет составлять Подобным образом, на член ренты R, внесенный в конце второго года, будут начисляться проценты 2 года. К концу срока ренты эта сумма будет составлять
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |


 .
. .
. .
. млн. руб. и
млн. руб. и  млн. руб. Фирма договорилась объединить оба платежа в один суммой
млн. руб. Фирма договорилась объединить оба платежа в один суммой  млн. руб. с продлением срока выплаты.
млн. руб. с продлением срока выплаты. , где P
, где P  -современная величина консолидируемых платежей.
-современная величина консолидируемых платежей.  млн. руб.
млн. руб.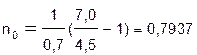 года
года
 и
и  наращиваются.
наращиваются.
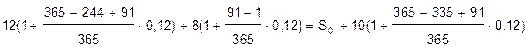
 млн. руб.
млн. руб.


 .
. . И т. д.
. И т. д.




