Потоки платежей (cash flows). Финансовые ренты

 

Контракты, сделки, производственно-хозяйственная деятельность, инвестиционные проекты часто предусматривают не отдельные разовые платежи, а множество распределенных во времени выплат и поступлений. Например: получение и погашение кредита, погашение задолженности, инвестиционный процесс, арендные платежи, получение процентов по ценным бумагам, выплата заработной платы, плата за квартиру и коммунальные услуги, откладывание на покупку автомобиля или другого предмета длительного пользования и т. д. Учитывая распространенность этих процессов можно сделать вывод о необходимости и важности изучения денежных потоков.

Потоком платежей (cash flows) называется последовательность величин самих платежей R_k, (со своими знаками) и моментов времени t_k, когда они осуществляются. Пусть CF = {R_k, t_k} – поток платежей и известна ставка процента i, обычно неизменная в течении всего потока (рис. 2).

Величиной потока платежей в момент Т называется сумма платежей потока, приведенных к этому моменту − CF(T) = ∑ R_k(1+i)^{T– t}_k.

CF +

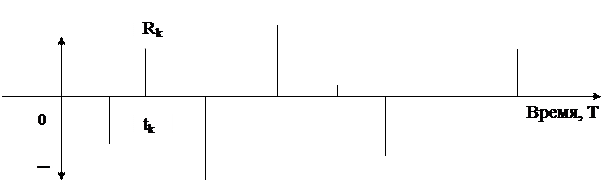
Рис. 2. Поток платежей

 

Достаточно найти величину потока в какой то момент времени CF(T₁), тогда в любой другой момент Т₂ величина потока CF(T₂) = CF(T₁) (1+i)^T₂^{– T}₁.

Величина CF(0) называется современной величиной потока; если есть последний платеж, то величина потока в момент этого платежа называется конечной величиной потока CF(T).

Потоки платежей могут быть: регулярными (с постоянным шагом расчета t) и нерегулярными, конечными и бесконечными, авансовыми (пренумерандо, антисипативными, то есть платежи осуществляются в начале временного отрезка) и обычными (постнумерандо, декурсивными, когда платежи осуществляются в конце временного отрезка), с постоянной ставкой процентов и с переменной ставкой, немедленными и отложенными, верными (безусловными) и условными (обусловленными каким либо событием), дискретными и непрерывными, по периодам платежей р, годовыми − р=1, полугодовыми р=2, поквартальными р=4, помесячными р=12, ежедневными, по периодам начисления m (от дискретных m =1, 2, 4, 12, 360 до непрерывных m =∞), ординарными (меняющими знак один раз) и неординарными (меняющими знак более одного раза).

Пример 8. Пусть денежный поток платежей равен CF(t) = {−2000, 1; −1000,2; 1000, 3; 3000, 5} (рис. 3), ставка процента i = 10% годовых.

 

а) Дать характеристику денежного потока.

б) Определить современную и конечную стоимость потока постнумерандо и пренумерандо.

Рис. 3. Поток денежных платежей

Решение.

а) Характеристику потока дать самостоятельно.

…

 

 

б) Современная стоимость потока постнумерандо равна:

CF(0) = ∑ R_t(1+i)^{– t} = 2000∙1.1^–1 −1000∙1,1^–2 +1000∙1,1^–3 +3000∙1,1^–5 = −30,6.

 

Конечная стоимость потока постнумерандо равна

CF(Т) = ∑ R_t(1+i)^{Т– t} = 2000∙1.1⁴ −1000∙1,1³ +1000∙1,1² +3000∙1,1⁰ = −49,2.

 

Конечную стоимость потока можно определить быстрее, используя известную формулу (2) для разовых платежей

CF(Т) = CF(0)(1+i)^–t = –30,6∙1,1 ^–5 = −49,2.

 

В случае платежей пренумерандо современная стоимость денежного потока равна CF_пренум(0) = CF_{постнум}(0)(1+i) = ∑ R_t(1+i)^{– t} (1+i) = −30.6∙(1+0.1) = −33.6.

 

В случае платежей пренумерандо конечная стоимость денежного потока равна CF_пренум(Т) = CF_{постнум}(Т)(1+i) = ∑ R_t(1+i)^{Т – t}(1+i) = −49,2∙(1+0.1) = −54,1.

 

Из данного примера следует, что потоки денежных платежей очень разнообразны, для нахождения стоимости потока платежей необходимо привести каждый платеж к одному моменту времени и затем алгебраически сложить. Наращенная и современная стоимость денежного потока находятся в такой же временной связи, как и разовые отдельные платежи. Авансовые платежи (платежи пренумерандо) увеличивают и современную и конечную стоимость потока в (1+i) раз.

Поток платежей, все члены которого положительные (однонаправленные) величины, а временные интервалы между ними постоянны (одинаковы) называется финансовой рентой (рентой, аннуитетом). То есть, рента является частным случаем потока денежных платежей в общем виде и представляет собой регулярный положительный (однонаправленный) поток платежей. На практике это регулярно получаемый доход на капитал, облигации, имущество или землю.

Основными параметрами ренты являются:

1) Член ренты R_t (величина платежа);

2) Период ренты t (временной интервал между платежами, шаг расчета);

3) Срок ренты Т или n (горизонт расчета);

4) Процентная ставка i.

Дополнительными параметрами ренты могут быть:

1) p − число платежей в году;

2) m − число начислений процентов в году.

Если R годовой рентный платеж, то сумма отдельного платежа равна R/p.

Рассмотрим сначала наиболее простую ренту (постоянная конечная рента), когда величина рентного платежа R постоянна, срок ренты − n периодов, известна процентная ставка i. На рентные платежи начисляются сложные проценты.

Для определения современной (текущей) и конечной (наращенной) стоимости ренты воспользуемся уже рассмотренными зависимостями для произвольных потоков платежей.

Современная стоимость ренты, как денежного потока равна

S₀ = CF(0) = R_t(1+i)^{– t} ,

при постоянном значении рентного платежа R_t = R его можно вынести за знак суммы S₀ = R ∑(1+i)^{– t},

в этом случае выражение под знаком суммы представляет собой n членов убывающей геометрической прогрессии с первым членом (1+i)^–1 и знаменателем (1+i)^–1. Как известно из курса элементарной математики сумма членов убывающей геометрической прогрессии равна [1– (1+i)^{– n}]/i.

Тогда формула для нахождения современной стоимости ренты имеет вид

S₀ = R[1− (1+i)^{– n} ]/i. (4)

Зная современную (начальную) величину ренты, можно легко найти её конечную (наращенную) величину.

S_n= S₀ (1+i) ⁿ = R[(1+i) ⁿ−1]/i. (5)

 

Величины [(1+i) ⁿ −1]/i = F₃ (i,n) и [1− (1+i)^{– n}]/i = F₄ (i,n) в формулах (5) и (4) называются соответственно коэффициентом наращения ренты и коэффициентом приведения ренты. В силу их частой употребительности они табулированы (см. приложение).

Если платежи поступают в конце очередного промежутка, то рента называется постнумерандо, в начале − пренумерандо. Обычно в условиях задачи по умолчанию предполагаются платежи постнумерандо.

Пример 9. Рассмотрим 5- летнюю ренту с годовым платежом R = 1000 руб., процентная ставка i = 10%.

 

Периоды расчета 1 2 3 4 5

Годовые платежи 1000 1000 1000 1000 1000

Суммы с процентами 1100 2310 3641 5105

Всего на счете 1000 2100 3310 4641 6105

 

Поясним движение денежных сумм.

 

В конце 1-го года в банк вносится 1000 руб. В конце 2-го года эта сумма возрастает до 1100 руб. за счет начисленных 10%. Вместе с очередным внесенным платежом в 1000 руб. на счете уже 2100. В конце 3-го года эта сумма возрастает до 2310 руб. за счет начисленных 10%. Вместе с очередным внесенным платежом на счете теперь уже 3310 руб. и т.д. Итоговая наращенная сумма ренты равна 6105 руб.

 

Конечную стоимость ренты можно вычислить быстрее, воспользовавшись формулой (5).

 

S_n= R[(1+i)ⁿ−1]/i = 1000[(1+0,1)⁵−1]/0,1 = 1000 F₃ (0,1;5) = 1000∙6.105 = 6105 руб.

 

Начальная стоимость ренты определится по формуле (4).

 

S₀= R[1− (1+i)^–n]/i = 1000[1− (1+0,1)^–5]/0,1 = 1000 F₄ (0,1;5) = 1000∙3,791 = 3791 руб.

 

или S₀= S_n (1+i)^–n = 6105∙1,1^–5 = 6105∙0,621 = 3791 руб.

 

Если платежи поступают вначале временного отрезка (пренумерандо), то конечная и начальная стоимость ренты будут соответственно равны

 

S_{n,пренум} = S_{n,постнум}(1+i) = 6105(1+i) = 6105∙1,1 = 6716 руб.

 

S_{0,пренум} = S_{0,постнум}(1+i) = 3791(1+i) = 3791∙1,1 = 4170 руб. или

 

S_{0,пренум} = S_{n,пренум} (1+i)^{– n} = 6716(1+0,1)^–5 = 6716∙1.1^–5 = 6716∙0.621 = 4170 руб.

 

Задачи для самостоятельного решения

Задача 6.. Найти современную и наращенную величину денежного потока платежей CF(t) = {−2000, 1; 1000,2; 1000, 3; 1000, 4}, при ставке процента i = 5% годовых.

Решение.

 

 

Задача 7. Создается фонд в течение n = 10 лет, взносы в который составляют R = 40 тыс. руб. в год. На собранные средства начисляются проценты по ставке i =10% годовых. Найти размер фонда?

Решение.

 

Задача 8. Имея обязательство на n =10 лет ежегодно выплачивать R =5000 руб. гражданин решил погасить его единовременно. Сколько необходимо заплатить при годовой ставке i =10%.

Решение.

 

 

Задача 9. В ходе судебного разбирательства выяснилось, что гражданин N ежемесячно недоплачивал налогов 100 руб. Налоговая инспекция хочет взыскать за 2 года с процентами (ставка i = 0,03 1/мес.). Сколько придется заплатить?

Решение.

 

Задача 10. По вине пенсионного фонда гражданину недоплачивали к пенсии 100 руб. ежемесячно в течение 10 лет. Суд обязал выплатить задолженность с процентами (номинальная годовая ставка j = 12%). Сколько получит пенсионер?

Решение.

 

Задача 11. Семья хочет накопить на дачу S_n = 12000 долл. За n = 6 лет. Какую сумму R (одинаковую) необходимо ежегодно откладывать, если годовая ставка процента i = 8%.

Решение.

Основные выводы по теме

 

1. Для нахождения стоимости потока платежей необходимо привести каждый платеж к одному моменту времени и затем их алгебраически сложить (не правильно складывать неприведенные платежи).

2. Наращенная и современная стоимость денежного потока находятся в такой же временной связи, как и разовые отдельные платежи (отличаются в (1+i)^T раз).

3. Авансовые платежи (платежи пренумерандо) увеличивают и современную и конечную стоимость потока в (1+i) раз.

4. Стоимость постоянной ренты равна сумме членов геометрической прогрессии. Для конечной стоимости ренты − возрастающая прогрессия. Для начальной стоимости ренты − убывающая прогрессия.

5. Коэффициент наращения постоянной конечной ренты показывает во сколько раз конечная (наращенная) стоимость ренты больше её рентного платежа и является будущей стоимостью единичного денежного потока, длящегося n периодов с процентной ставкой i.

6. Коэффициент приведения постоянной конечной ренты показывает во сколько раз начальная (дисконтированная) стоимость ренты больше её рентного платежа и является современной стоимостью единичного денежного потока, длящегося n периодов с процентной ставкой i.

7. Перенос рентных платежей в начало периода (платежи пренумерандо) увеличивают стоимость ренты в (1+i) раз.