Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение наращенной стоимости годовой финансовой рентыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть задан регулярный финансовый поток постнумерандо. Суммарный годовой платеж обозначим Наращенные отдельные платежи представляют собой геометрическую прогрессию с первым членом Определим наращенную стоимость ренты
Выражение Рассмотрим финансовую ренту пренумерандо, т.е. платежи осуществляются вначале каждого периода. Следовательно, число раз наращения каждого платежа на один раз больше, что дает увеличение каждого платежа в
следовательно, в этом случае ·∙ I Пример. В течение 4 лет ежегодно в конце года на специальный счет поступает 50 тыс. руб. Определить наращенную стоимость начисления сложных процентов по ставке 10%. Решение: Рента постнумерандо;
Пример. Создается целевой фонд для обеспечения инвестиций в сумме 10 млн. руб. сроком на 5 лет, процентная ставка 20%. Определить ежегодные платежи пренумерандо. Решение:
Наращенная сумма годовой ренты с начислением процентов M раз в год Рассмотрим случай, капитализация процентов осуществляется чаще, чем один раз в год. Предположим, проценты начисляются m раз в год. В этом случае их каждый раз начисляют по ставке Наращенные платежи представляют собой геометрическую прогрессию с первым членом R и знаменателем прогрессии
Наращенная сумма такой ренты определяется по формуле:
где R- размер годового платежа. Пример. На банковский счет ежегодно в конце года поступает 10 000 рублей в течение 7 лет. На эти средства ежеквартально начисляют проценты по номинальной ставке 15% годовых. Определить, какая сумма будет на банковском счете к концу срока. Решение: R=10 000 руб.; m = 4 раза в год; n =7 лет; i = 0, 15.
Наращенная величина р-срочной ренты
Предположим, что вложение средств и капитализация процентов осуществляются чаще,чем один раз в год. Пусть
Тогда платеж за период Число процентных периодов Наращенные платежи представляют собой геометрическую прогрессию с первым членом Количество членов ренты равно р·n. Найдем ее сумму:
Для ренты пренумерандо: Пример. Страховая компания принимает платежи по полугодиям равными частями по 250 тыс. руб. в течение 3 лет. Банк, обслуживающий компанию, начисляет проценты ежеквартально из расчета 10% годовых. Определить, какую сумму получит страховая компания по истечению срока договора. Решение:
Пример. Для обеспечения некоторых будущих расходов создается фонд средств. В фонд поступают платежи в виде постоянной годовой ренты постнумерандо в течение 5 лет. Размер разового платежа 4 млн. руб. На поступившие взносы начисляются проценты по ставке 18,5% годовых. Найти величину фонда на конец срока, если 1). Проценты начисляются, и платежи выплачиваются один раз в год.( R = 4 млн.руб.; i = 18,5% годовых; n=5 лет.
2). Проценты начисляются поквартально, платежи осуществляются один раз в год (
Переход от годового начисления процентов к поквартальному несколько увеличил наращенную сумму. 3). Допустим, проценты начисляются раз в год, платежи выплачиваются поквартально. (
4). Пусть платежи и начисление процентов производятся поквартально. (m = p = 4);
5). Пусть платежи производятся поквартально, а начисление процентов производится ежемесячно (
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 4146; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.111 (0.007 с.) |

 . Предположим, что начисление процентов и осуществление платежей производится один раз в год.
. Предположим, что начисление процентов и осуществление платежей производится один раз в год. , где
, где  - процентная ставка.
- процентная ставка. , как сумму геометрической прогрессии:
, как сумму геометрической прогрессии: ; (6.1)
; (6.1) называют коэффициентом или множителем наращения финансовой ренты. Он представляет собой стоимость регулярного потока платежей, каждый из которых равен одной денежной единице к моменту окончания всех платежей. Значения множителей наращения ренты
называют коэффициентом или множителем наращения финансовой ренты. Он представляет собой стоимость регулярного потока платежей, каждый из которых равен одной денежной единице к моменту окончания всех платежей. Значения множителей наращения ренты 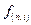 приведены в приложении 4.
приведены в приложении 4.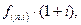
 (6.2)
(6.2) = 4,
= 4, 

 Найти
Найти 
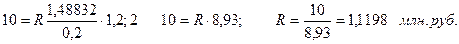
 , где i - номинальная ставка процентов. Срок ренты n лет.
, где i - номинальная ставка процентов. Срок ренты n лет. .
. (6.3)
(6.3)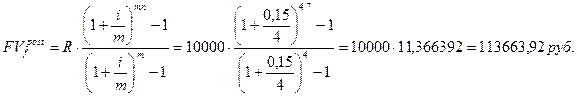
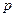 – число платежей в год;
– число платежей в год; – количество начислений процентов.
– количество начислений процентов.
 , по ставке
, по ставке  .
. (6.4)
(6.4) (6.5)
(6.5)
 ).
).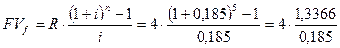 =28,90 млн. руб.
=28,90 млн. руб.