
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Годовая рента, начисление процентов m раз в году.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Посмотрим, как усложнится формула, если предположить теперь, что платежи делают один раз в конце года, а проценты начисляют m раз в году.
1.3.3. Рента p-срочная, m=1 Найдем наращенную сумму при условии, что рента выплачивается p раз в году равными платежами, а проценты начисляются один раз в конце года.
1.3.4. Рента p-срочная, p=m В контрактах часто начисление процентов и поступление платежа совпадают во времени. Таким образом число платежей p в году и число начислений процентов m совпадают, т.е. p=m. Тогда для получения формулы расчета наращенной суммы можно воспользоваться аналогией с годовой рентой и одноразовым начислением процентов в конце года, для которой Различие будет лишь в том, что все параметры теперь характеризуют ставку и платеж за период, а не за год. Таким образом получаем
1.3.5. Рента p-срочная, р ≥ 1, m ≥ 1. Это самый общий случай p -срочной ренты с начислением процентов m раз в году, причем, возможно p ≥ m. Получаем наращенную сумму
Отметим, что из нее легко получить все рассмотренные выше частные случаи, задавая соответствующие значения p и m. Формулы современной величины Обычная годовая рента Пусть член годовой ренты равен R, процентная ставка i, проценты начисляются один раз в конце года, срок ренты n. Тогда дисконтированная величина первого платежа равна
Приведенная к началу ренты величина второго платежа равна Rn 2 и т.д. В итоге приведенные величины образуют геометрическую прогрессию: Rn, Rn 2,Rn 3,..., R nn, сумма которой равна
где Как видим, коэффициент приведения ренты зависит только от двух параметров: срока ренты n и процентной ставки i. 5.4.2. Рента p-срочная, р ≥ 1, m ≥ 1. Аналогичные рассуждения позволяют получить формулу для расчета современной величины ренты в самом общем случае для произвольных значений p и m
от которой нетрудно перейти к частным случаям при различных p и m. Зависимость между современной величиной и наращенной суммой ренты
Пусть A - современная величина годовой ренты постнумерандо, а S - ее наращенная стоимость к концу срока n, p=1, m=1. Покажем, что наращение процентов на сумму A за n лет дает сумму, равную S:
Отсюда же следует, что дисконтирование S дает A: а коэффициент дисконтирования и наращения ренты связаны соотношениями:
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.28.56 (0.009 с.) |

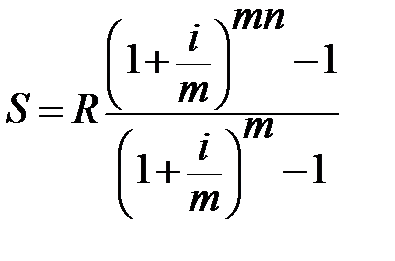 - по схеме постнумерандо.
- по схеме постнумерандо. - по схеме пренумерандо. (1.3)
- по схеме пренумерандо. (1.3) - по схеме постнумерандо.
- по схеме постнумерандо. - по схеме пренумерандо. (1.4)
- по схеме пренумерандо. (1.4)
 - по схеме постнумерандо.
- по схеме постнумерандо. - по схеме пренумерандо. (1.5)
- по схеме пренумерандо. (1.5) - по схеме постнумерандо.
- по схеме постнумерандо. - по схеме пренумерандо. (1.6)
- по схеме пренумерандо. (1.6)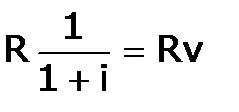 , где
, где  - дисконтный множитель.
- дисконтный множитель. , (1.7)
, (1.7) (1.8) - коэффициент приведения ренты.
(1.8) - коэффициент приведения ренты.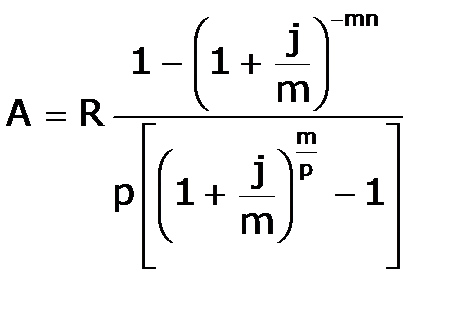 , (1.9)
, (1.9) (1.10)
(1.10)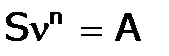 , (1.11)
, (1.11) (1.12)
(1.12)  . (1.13)
. (1.13)


