
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение процентов в банковской практике.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Начисление процентов на вклад по простой и сложной схеме Очень важную роль играют проценты в банковских расчетах. Размер прибыли, которую вам начислят по вкладу через год, зависит от размера вклада – чем больше вклад, тем больше прибыль. Для разных типов вкладов (пенсионный, срочный, валютный и т.д.) банк объявляет процент годовой прибыли по вкладу выбранного вами типа. Например, для пенсионного вклада – это 8% годовых, для простого – 5% годовых, для валютного - 6% и т.д. В общем случае процент годовой прибыли обозначим через р. Это означает, что на каждый вложенный рубль (для валютного вклада - доллар) через год банком вам будет начислена прибыль в размере р копеек (или для валютного вклада – центов). Тем самым, через год на вашем счету вместо рубля (доллара), окажется
Такая схема начисления процентов называется сложной. Начисление процентов называется простым (простые проценты), если начисление процентов производится каждый раз только на первоначальную сумму, а на прибыль не производится. Указанная схема соответствует, например, такой ситуации. Вы кладете в банк S рублей под р% годовых. В конце года вам начисляется прибыль, вы ее снимаете и ваш первоначальный вклад сохраняется. На следующий год вы опять снимаете прибыль и так поступаете каждый год в течение n лет. Если вы через n лет снимете и вклад S, то окажется, что, положив в банк S рублей на n лет, вы получили возможность распорядиться суммой в Для того, чтобы вклад не обесценивался из-за инфляции ставка процента i должна быть больше темпа инфляции.
Использование приближенных формул и таблиц, когда n велико Расчеты по формулам сложных процентов при больших n становятся затруднительными. В этом случае хорошую оценку наращенного значения позволяет получить следующая формула, верная при больших значениях х:
Значок» означает в данном случае, что чем больше х, тем меньше разница между правой и левой частью выражения. Эту же формулу можно записать следующим образом:
С помощью элементарного преобразования из этих формул можно получить такие формулы:
Пример Вклад величины S положен в банк под 5% годовых. Начисление процентов производится в конце года от всей накопившейся суммы (сложная схема). Во сколько раз увеличится вклад через 20 лет, через 40 лет? Решение: S20=S(1+0,05)20=S(1+5:100)100:5»S×e S40=S(1+0,05)40=S(1+5:100)(100: 5)×2»S×e2 Т. е., за 20 лет вклад вырастет примерно в е»2,72 раза, за 40 лет в е2»7,39 раз.
Для облегчения расчетов создано множество таблиц и пакетов прикладных программ. В качестве примера приводим таблицу, в которой указаны значения множителя наращения Такая таблица не только избавляет от вычисления высоких степеней в задаче вычисления накопленного капитала, но и позволяет дать оценки при решении обратной задачи – за сколько периодов капитал увеличится в k раз. Таблица демонстрирует быстрый рост множителя наращения при больших n (капитал лежит очень много лет). Попробуем с помощью таблицы оценить, каким стал, например, такой вклад. Царское правительство во время 1-ой мировой войны в счет платы за закупленное за рубежом оружие переправило в банки Японии и ряда других стран большое количество золота. Оружие получено не было, вклады остались в банках. Переправлялся за границу и государственный золотой запас России, составлявший 2,5 тыс. тонн золота. В современных ценах это примерно $40 млрд. С тех пор прошло больше 80 лет. Таблица позволяет оценить, во сколько раз увеличилась за это время вложенная сумма. При росте на 6% в год эта сумма выросла в 100 раз. Некоторые эксперты оценивают современную стоимость вклада в 4 триллиона долларов, что и демонстрирует наша таблица (стоит заметить, что ни судьба, ни сумма вкладов неизвестны). Или такой пример. 350 лет назад за остров Манхеттен было уплачено 24 доллара. Современная его стоимость 40млрд. долларов. То есть за 350 лет произошло увеличение его стоимости в 1,7млрд. раз. Какой годовой ставке процента соответствует такой рост? Таблица (более подробная, чем наша) показывает, что эта ставка приблизительно равна 6% (точный ответ – 6,3%). Таблица 1: Множители наращения (сложные проценты) (1 +
У всех на памяти последняя денежная реформа в нашей стране, позволившая избавиться от трех нулей во всех ценах. В течение нескольких лет имела место высокая ежемесячная инфляция, что привело к росту цен более, чем в 1000 раз. Из таблицы находим, что множитель наращения 1000 соответствует средней инфляции в 15% в месяц в течение 50 периодов (4 года), или инфляции 12% в течение 60 периодов (5 лет). Заодно определяем, что инфляция 15% в месяц – это увеличение цен за год в 4,05×1,32=5,35 раз, а для 12% в месяц – в 3,11×1,25=3,89 раз. Примеры 1. 20000 рублей положили в банк под 12% годовых. Какая сумма окажется на счету через 8 лет? Взяли в долг 20000 рублей с возвратом через 8 лет под 12% годовых. Сколько надо уплатить через 8 лет? (второй вариант той же задачи). Решение: Находим из таблицы, что капитал увеличится в 2,48 раза. (число 2,48 стоит на пересечении строки - число периодов 8 и столбца – годовая ставка 12%). Следовательно, через 8 лет вклад станет равным (надо будет вернуть): 20000×2,48=49600 рублей. 2. Какая должна быть ставка процента, чтобы капитал за 10 лет увеличился примерно в 1,5 раза? Решение: В строке, соответствующей 10 годам увеличение капитала в 1,48 раз находится в столбце, соответствующем годовой ставке 4%.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 799; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.007 с.) |

 рублей (долларов), а вместо S рублей (долларов)
рублей (долларов), а вместо S рублей (долларов)  рублей (долларов). В задачах из банковской сферы величина
рублей (долларов). В задачах из банковской сферы величина  называется ставкой наращения. Если вы не снимете свой вклад еще год, то ваш увеличившийся вклад S1 вырастет еще на р процентов и через 2 года у вас на счету окажется:
называется ставкой наращения. Если вы не снимете свой вклад еще год, то ваш увеличившийся вклад S1 вырастет еще на р процентов и через 2 года у вас на счету окажется: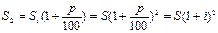 рублей (долларов), а через n лет
рублей (долларов), а через n лет 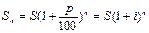 рублей (долларов).
рублей (долларов). рублей, из которых S рублей – ваши деньги, а Sni – насчитанная на них прибыль.
рублей, из которых S рублей – ваши деньги, а Sni – насчитанная на них прибыль. , где е =2,7182818… - одна из важнейших констант в математике.
, где е =2,7182818… - одна из важнейших констант в математике. , но уже если значение у мало.
, но уже если значение у мало.
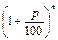 , использующегося в формулах наращения по сложным процентам для наиболее часто используемых процентов и числа периодов наращения n.
, использующегося в формулах наращения по сложным процентам для наиболее часто используемых процентов и числа периодов наращения n.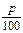 )n
)n


