
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь между декартовыми координатами и полярнымиСодержание книги
Поиск на нашем сайте
Часто можно легко выписать формулу, показывающую, как изменятся координаты точки М, если от одной системы координат перейти к другой. Выведем формулы связи между декартовыми координатами (x,y) и полярными r и φ. Пусть даны: декартова система координат и полярная с полюсом в начале координат и полярной осью, совпадающей с осью X (рис. 7а), x и y – декартовы координаты точки, r и φ – ее полярные координаты. Из треугольника, образованного точками О, М и х, видно, что зависимость между полярными координатами r и φ точки М и ее прямоугольными координатами x и y выражается формулами, известными из тригонометрии: y =rsinj, x =rcosj - вычисление декартовых координат по полярным
То есть, зная декартовы координаты точки, мы можем определить ее полярные координаты. И наоборот. Зная ее полярные координаты, можно определить декартовы координаты.
Пример Чему равны полярные координаты точки М, имеющей декартовы координаты один и минус один? Подставив значения декартовых координат в формулы, которые задают выражение полярных координат через декартовы, получаем, что:
Так как точка М находится в четвертой четверти, то j=315° (рис. 7б)
Линии и их уравнения Итак, при наличии системы координат каждой точке плоскости соответствует пара действительных чисел и, наоборот, каждой паре чисел соответствует определенная точка плоскости. Можно установить, что линиям на плоскости соответствует некоторое уравнение с двумя переменными x и y в декартовой системе координат и переменными r и j в полярной. Связь между уравнениями и линиями позволяет свести изучение геометрических свойств линий к исследованию аналитических свойств соответствующих им уравнений. Линии на плоскости соответствует некоторое уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней. Такое уравнение называют уравнением данной линии. Входящие в него координаты x и y (или r и j) произвольной точки линии называются текущими координатами. Уравнение линии на плоскости может быть аналитически задано в явном виде - y=f(x), r=f(j) или неявном виде - F(x,y)=0, F(r,j)=0. Полярную систему координат удобно использовать, когда длина радиуса-вектора точек, лежащих на линии, связана аналитической зависимостью со значением угла поворота j.
Примеры уравнений линий в декартовой и полярной системе координат 1.Уравнение прямой, отсекающей на оси Y отрезок величины b: y=kx+b, где k - значение tg угла наклона прямой к оси ОХ; параметр k называется угловым коэффициентом прямой. Уравнение линии задано в явном виде (рис. 8). 2.Уравнение линии, являющейся геометрическим местом точек, для которых расстояние до некоторой точки О с координатами а и b есть величина постоянная (обозначим ее через R). Выпишем условие равенства константе R расстояния от любой точки М(x,y) до точки O(a,b): (x-a)2+(y-b)2=R2 Если система координат выбрана так, что центр окружности совпадает с началом координат, то a=0, b=0 и уравнение окружности принимает вид: x2+y2=R2 Уравнение линии в этих примерах задано в неявном виде. 3.Уравнение окружности в полярной системе координат. Введем полярную систему координат, центр которой совпадает с центром окружности, а направление полярной оси, например, горизонтальное. Окружность определяется, как геометрическое место точек, для которых расстояние до некоторой точки О есть величина постоянная (эту величину мы обозначали через R). Следовательно, уравнение окружности в полярных координатах: r=R Окружность дает простейший пример линии, уравнение которой от перехода к полярной системе координат упрощается.
На рисунке 9 приведена окружность и ее уравнение в разных системах координат. Одновременно мы показали на этом простом примере, что вид линии не зависит от того, в какой системе координат написано ее уравнение. От выбора системы координат зависит лишь вид уравнения. Рассмотрим примеры еще 2 кривых, длина радиуса-вектора которых связана аналитической зависимостью со значением его угла поворота j. Уравнения этих кривых удобно задавать именно в полярной системе координат.
Уравнение спирали Архимеда Пусть по лучу, вращающемуся около полюса О с постоянной угловой скоростью w, движется точка М с постоянной скоростью v. Тогда точка М опишет линию, которая называется спиралью Архимеда. Для того чтобы вывести уравнение этой линии, введем полярную систему координат, центр которой совпадает с точкой О, тогда расстояние от точки М до полюса О r=ОМ пропорционально углу j (рис 10а). Это означает, что уравнение спирали Архимеда можно записать в виде: r=kj. В предыдущих главах мы строили опорные точки графика спирали Архимеда, руководствуясь именно этим свойством спирали – при изменении угла на величину nΔφ длину радиуса-вектора мы меняли на nΔr.
Из уравнения видно, что если j=2p (точка М совершила полный оборот вокруг центра О), то r1=k×2p, после второго оборота r2=k×4p=2r1, после третьего r3=k×6p=3r1 и т.д. Величина k×2p= а называется шагом спирали. Шаг спирали - это величина смещения вдоль луча, соответствующее повороту луча на 2p. Так как шаг спирали имеет ясный физический смысл, уравнение спирали Архимеда принято задавать в терминах именно шага спирали:
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2926; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.161 (0.007 с.) |

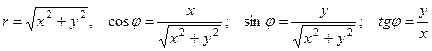 - вычисление полярных координат по декартовым (одной формулы для определения угла недостаточно).
- вычисление полярных координат по декартовым (одной формулы для определения угла недостаточно).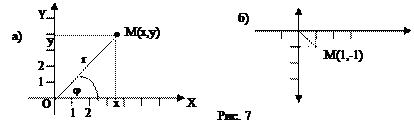
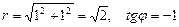
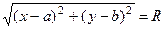 . Возведя обе части равенства в квадрат, получаем каноническое уравнение окружности:
. Возведя обе части равенства в квадрат, получаем каноническое уравнение окружности:

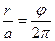 . Коэффициент пропорциональности k и шаг спирали а связаны соотношением:
. Коэффициент пропорциональности k и шаг спирали а связаны соотношением:  и а=2pk.
и а=2pk.


