
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конические сечения (коники). Кривые 2-го порядкаСодержание книги
Поиск на нашем сайте
Гипербола Построим график гиперболы
В общем случае каноническое уравнение гиперболы имеет вид: Уравнения асимптот: Прямая, на которой лежат фокусы, называется вещественной осью. Число а называют вещественной полуосью, а число b - мнимой полуосью гиперболы. Фокусами гиперболы служат точки F1 и F2 с координатами (- c, 0) и (c,0), соответственно. Фокусное расстояние c вычисляется по значениям полуосей гиперболы по формуле: Отношение На рисунке 2б показано построение опорных точек М1 и М2 гиперболы по заданным вершинам А и В и фокусам F1 и F2 гиперболы. Правило построения: R2-R1=2 a.
Парабола Параболой, называется линия, уравнение которой у=ах2 (это уравнение параболы называется каноническим). Она изображена на рисунке 3а. Парабола определяется, как геометрическое место точек, для которых расстояния до фиксированной точки F плоскости, называемой фокусом параболы и прямой d, называемой директрисой, равны друг другу. Если выбрать систему координат так, чтобы вершина параболы попала в начало координат О, а директриса была параллельна оси Х, то фокус F будет лежать на оси Y.
Если расстояние от точки F до прямой d обозначить через р, то расстояние от фокуса до вершины равно р/2 и уравнение параболы будет иметь вид: На рисунке 3в приведен способ построения параболы по вершине О и точке М.
Фокус параболы безопасности совпадает с общей точкой всех парабол (конец орудийного ствола). Она касается общей директрисы всех траекторий. Если изогнуть узкую полоску металла по дуге параболы, то лучи точечного источника света, помещенного в фокусе, отразившись от полоски, пойдут параллельно оси (рис. 3г). Обратно, если на эту полоску будет падать пучок лучей, параллельный оси параболы, то после отражения лучи соберутся в ее фокусе (слово focus в переводе с латинского означает "огонь"). На этом основано свойство параболических зеркал в автомобильных фарах и прожекторах и устройство телескопов. Зеркала прожекторов и телескопов шлифуются по параболоиду, получающемуся от вращения параболы.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 547; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.158.29 (0.006 с.) |

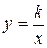 (или ху=k) с помощью растяжения вдоль оси Y графика гиперболы
(или ху=k) с помощью растяжения вдоль оси Y графика гиперболы  , затем повернем оси координат на 45° (рис.1). При замене координат
, затем повернем оси координат на 45° (рис.1). При замене координат  уравнение ху=k обратится в уравнение (u-v)(u+v)=2k или u2-v2=2k. Вернемся к привычным для абсциссы и ординаты обозначениям: х2-у2=2k. Таким образом, кривая
уравнение ху=k обратится в уравнение (u-v)(u+v)=2k или u2-v2=2k. Вернемся к привычным для абсциссы и ординаты обозначениям: х2-у2=2k. Таким образом, кривая 
 . Такое уравнение получается из уравнения
. Такое уравнение получается из уравнения  или
или  , если выполнить сжатие вдоль оси Y к оси Х с коэффициентом a/b. Гипербола определяется, как геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная 2 а. Изобразить гиперболу на плоскости можно так: построим характеристический прямоугольник с центром в начале координат и со сторонами длины 2 а и 2 b. Прямые, проходящие через диагонали этого прямоугольника, являются асимптотами гиперболы. С ростом x и y гипербола стремится приблизиться к асимптотам, но никогда их не пересекает. Гипербола пересекает ось X в точках, которые находятся на расстоянии а от начала координат. Эти точки называются вершинами гиперболы (точки А и В).
, если выполнить сжатие вдоль оси Y к оси Х с коэффициентом a/b. Гипербола определяется, как геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная, равная 2 а. Изобразить гиперболу на плоскости можно так: построим характеристический прямоугольник с центром в начале координат и со сторонами длины 2 а и 2 b. Прямые, проходящие через диагонали этого прямоугольника, являются асимптотами гиперболы. С ростом x и y гипербола стремится приблизиться к асимптотам, но никогда их не пересекает. Гипербола пересекает ось X в точках, которые находятся на расстоянии а от начала координат. Эти точки называются вершинами гиперболы (точки А и В). .
.
 , оно называется эксцентриситетом гиперболы.
, оно называется эксцентриситетом гиперболы.
 . Построение опорных точек параболы, если заданы ее фокус и директриса показаны на рисунке 3б. В основу построения положено равенство расстояний от точек параболы до фокуса и директрисы.
. Построение опорных точек параболы, если заданы ее фокус и директриса показаны на рисунке 3б. В основу построения положено равенство расстояний от точек параболы до фокуса и директрисы. Камень, брошенный не строго вертикально, летит по параболе. То же можно сказать и об орудийном снаряде. Форму параболы имеют струи фонтана. Для построения эскиза этих парабол можно воспользоваться методами, предложенными на рисунке 3. Траектории всех снарядов, имеющих одинаковое значение, но разное направление начальной скорости, имеют общую огибающую, которая также имеет форму параболы. Это так называемая парабола безопасности. Аналогично струи фонтана имеют огибающую "безопасности" (если вы будете стоять вне ее пределов, то Парабола Безопасности никакая струя до вас не долетит).
Камень, брошенный не строго вертикально, летит по параболе. То же можно сказать и об орудийном снаряде. Форму параболы имеют струи фонтана. Для построения эскиза этих парабол можно воспользоваться методами, предложенными на рисунке 3. Траектории всех снарядов, имеющих одинаковое значение, но разное направление начальной скорости, имеют общую огибающую, которая также имеет форму параболы. Это так называемая парабола безопасности. Аналогично струи фонтана имеют огибающую "безопасности" (если вы будете стоять вне ее пределов, то Парабола Безопасности никакая струя до вас не долетит).




