
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции. Точки разрыва функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим функцию непрерывного аргумента y =f(x). Пусть при приближении значения аргумента к числу а значение функции приближается к числу А как угодно близко (и может быть даже принимает значение А) (рис. 4). Тогда говорят, что в точке а существует предел функции f(x), равный А, и это записывается следующим образом:
Как а, так и А могут, вообще говоря, принимать значение, равное бесконечности (¥). В случаях, когда функция ведет себя по-разному, в зависимости от того, справа или слева мы приближаемся к точке а, говорят о пределе справа и пределе слева и приняты следующие обозначения:
Примеры 1. 2. 3.
Непрерывными являются функции y=x2, y =sin x, y=ax (на всей числовой прямой), y =ln x (при х >0) и т.д. Производная и ее геометрический смысл Производной функции y= f (x) в точке х 0 называется предел отношения приращения функции D y= f (x0+ D x)- f (x0) к приращению аргумента D х при произвольном стремлении D х к нулю, если такой предел существует. Обозначается производная функции f(x) в точке х 0 символом f'(x 0). Таким образом:
Можно использовать и другие обозначения: Примеры 1. y=kx. Возьмем произвольную точку х, и найдем значение соответствующего предела:
2. у=х 2.
Геометрический смысл производной состоит в том, что угловой коэффициент касательной, проведенной к кривой f(x) в точке х 0, есть f'(x0) (рис. 11) и, следовательно, уравнение касательной к графику в точке М0, имеет вид: y-y0=k(x-x0)=f'(x0)(x-x0).
Если функция в некоторой точке х0 имеет производную, то она в этой точке непрерывна. Это следует из соотношения:
Отсюда D у~f'(x0) D x и D у ®0 при D х ®0, то есть: f(x0 +D x)® f(x0) (D х ®0). Это же соотношение можно переписать так: f(x0+ D x)- f(x0)~f'(x0) D x, или f(x0 +D x)~f(x0)+f'(x0) D x Линейная часть приращения функции, выражающаяся через производную, называется дифференциалом функции. Он обозначается dy. Полное приращение D у в точках, в которых существует производная, можно представить в виде: D у=f(x +D x)-f(x)=f'(x) D x+a( D x), где a (D х)<<D x (<< означает много меньше). dy=f'(x) D x=f'(x)dx (D x=dx - дифференциал аргумента равен приращению аргумента).
Основные правила дифференцирования Мы показали, как вычисляется производная функции y=kx. Это лишь самые простой пример вычисления производной. Применяя похожие рассуждения, можно найти производные всех основных элементарных функций. Приведем таблицу этих производных.
Таблица основных формул дифференцирования. 1. y=c, y'=0, c – постоянная 2. y=xa, y'=a×xa-1 (a¹ 0), для целого n y=xn, y'= n x n-1 и 3. y=ax, y' = ax ln a, если a=e и y=ex, y'=ex 4. y =log ax, 5. y=sinx, y'=cosx, у=arcsinx, 6. y=cosx, y'=-sinx, у=arccosx, 7. y=tgx, 8. y=ctgx,
Для вычисления производных сложных функций и функций, получающихся из основных с помощью сложения, вычитания, умножения и деления, надо руководствоваться следующими правилами. Если функции u(x) и v(x) дифференцируемы в точке х, тогда справедливы следующие правила дифференцирования: 1. (cu),'=c×u', где с – постоянная; 2. (u±v)=u'±v'; 3. (u×v)'=u'v+v'u; 4. 5. Если y=f(u), и u=j(x), то есть у есть сложная функция от х: y=f(j(x)), то:
Если y=f(u), u=j(t), t=y(x), то Примеры y= 2 ex+ 3ln x- 5; y'= 2 ex+ 3×1 /x. y=x ex, y'=(x)' ex+x×(ex)'=ex+xex=ex( 1 +x)
Производные высших порядков Пусть f'(x) есть производная от функции f(x). Тогда производная от функции f'(x) называется второй производной (или производной второго порядка) от функции f(x) и обозначается f''(x). Третья производная - это производная от второй производной и т.д. - n-ая производная - это производная от n-1-ой производной.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 или
или 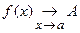


 (рис. 5а)
(рис. 5а) (рис. 5б)
(рис. 5б) (рис. 6). Заметим, что при стремлении j к p/2 слева, тангенс неограниченно возрастает, а при стремлении j к p/2 справа, тангенс неограниченно убывает. Таким образом,
(рис. 6). Заметим, что при стремлении j к p/2 слева, тангенс неограниченно возрастает, а при стремлении j к p/2 справа, тангенс неограниченно убывает. Таким образом, 
 На рисунках 7, 8 и 9 приведены графики функций, имеющих разрыв в точке х 0. На рисунке 10 приведен график функции, которая на отрезке [А,В] не имеет точек разрыва. Такая функция называется непрерывной на отрезке [А,В] (в каждой точке а отрезка функция имеет определенное значение b и
На рисунках 7, 8 и 9 приведены графики функций, имеющих разрыв в точке х 0. На рисунке 10 приведен график функции, которая на отрезке [А,В] не имеет точек разрыва. Такая функция называется непрерывной на отрезке [А,В] (в каждой точке а отрезка функция имеет определенное значение b и  ).
).
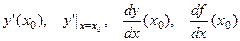


 Если вычислять производную в различных значениях х, принадлежащих некоторому множеству, например, отрезку [ a,b ], то величина ее будет зависеть от значения х. Тем самым, можно говорить о производной функции, определенной на этом множестве. Производную функции обозначают f'(x).
Если вычислять производную в различных значениях х, принадлежащих некоторому множеству, например, отрезку [ a,b ], то величина ее будет зависеть от значения х. Тем самым, можно говорить о производной функции, определенной на этом множестве. Производную функции обозначают f'(x).
 (х ¹0)
(х ¹0)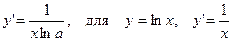


 , у=arctgx,
, у=arctgx, 
 , у=arcctgx,
, у=arcctgx, 


 - "цепное правило" (в случае "цепи" из большего числа функций поступают аналогично).
- "цепное правило" (в случае "цепи" из большего числа функций поступают аналогично).


