
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площадь поверхности вращенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим поверхность, полученную вращением вокруг оси ОХ дуги АВ, описываемой уравнением y=f(x) на интервале [a,b]. Разобьем, как мы это уже неоднократно проделывали, интервал [a,b] на n частей, восставим в точках деления перпендикуляры к оси ОХ и куски дуг Ds заменим прямыми отрезками, соединяющими концы дуг. Площадь поверхности вращения есть предел, к которому стремится площадь поверхности, образованной вращением ломаной линии, когда число звеньев ломаной неограниченно возрастает, а длины звеньев стремятся к нулю. В этом определении мы, как обычно, пользуемся эквивалентностью длины дуги и хорды (когда длина дуги мала). Для одной узкой полоски поверхности, площадь вычисляется по формуле: DSi~2pyds, где
Если поверхность образована вращением кривой вокруг оси OY, то все рассуждения сохраняются, но х и у меняются местами: DSi~2p х ds и переменной интегрирования будет у (рис. 10): Например, вычислим площадь поверхности шара (рис.11). В полярных координатах формула поверхности фигуры выглядит следующим образом:
Найдем площадь поверхности маковки, образованной вращением вокруг оси OY дуг окружностей. Рассмотрим два варианта. 1. Маковка состоит из сегмента высоты h шара радиуса R и, начиная с 60-ой параллели, - поверхности вращения дуги окружности того же радиуса R вокруг вертикали. Сопряжение дуг гладкое, они имеют общую касательную (рис. 12а).
Площадь сферической части маковки S1 ищется по известной формуле площади сегмента шара: S1=2pRh. Площадь верхней части маковки S2 – площадь поверхности вращения дуги окружности вокруг оси OY. С дугами окружности проще работать в полярной системе координат. Возьмем в качестве переменной интегрирования угол j (рис. 12б) и применим те же рассуждения. Выпишем, чему равна боковая поверхность узкой цилиндрической полоски. Величина радиуса цилиндра равна R-Rcosj=R(1-cosj). Величина образующей ds=Rdj. Следовательно,
В нашем конкретном случае точке перегиба, до которой мы интегрируем, соответствует значение j0=60°=p/3 (силуэт верхней части маковки состоит из 2-х дуг окружности, центральный угол которых равен 60°). S=S1+S2=2pRh+2pR2(p/3-sinp/3)=2pRh+2pR2(p/3- Для шлема вместо слагаемого 2pR2×0,18 по формуле S2=2pRh получается величина: 2pR2(1- 2. Маковка с раздвинутыми боками (рис. 13а). Для того чтобы найти поверхность такой маковки, выпишем формулу для вычисления поверхности вращения выпуклой дуги окружности, центр которой находится на расстоянии а от оси вращения. Такая поверхность не будет частью сферы. Это часть тора. Самый простой пример тора – хорошо всем известный бублик. Лежащий горизонтально бублик получается вращением вокруг вертикальной оси целой окружности. Если вращать не всю окружность, а только некоторую дугу окружности, то получится часть поверхности тора. Как видно из чертежа 13б величина радиуса узкого цилиндра, боковая поверхность которого нас интересует, равна а +Rcosj. Длина образующей ds=Rdj. Следовательно,
Для j0=60°=p/3 S2=2pRa×p/3+
Ответы к задачам Глава 1 1. 2,3515£x£2,399 х~2,4- 2 верных знака 2. 0,6% 3. 1260 4. 38,8% 5. 117,8£х£130 6. 44% 7. 2%, 3%, 4%, 5%; (1-0,01)n=0,99n 8. Валютный выгоднее 9. 1,052 10.»е20 копеек или е18 рублей, ≈е120копеек≈1,28∙1052 Глава 2 1. 6 2. 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024; 1, 2, 4, 8, 16, 32, 64, 128, 256, 512;
3. 4. 1, 0.6, 0.36, 0.216, 0.1296; 0.4, 0.24, 0.144; 0.0864; 1, 0.618, 0,382, 0.236, 0.146, 0.090; 0.382, 0.236, 0.146, 0.090, 0,056; 2.9%, 5.7%, 8,5%,11,1%; 5. 1, 1.6, 2.56, 4.096, 6.55; 2.6, 4.16, 6.66, 10.646; 1, 1.618, 2.618, 4.236, 6.854; 2.618, 4.236, 6.854; Глава 4 3. 10м 4. 21,5м; 43м 5. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 13. 1, 1.272, 1.618, 2,058, 2,618 18. 1.618 19. Глава 7 1. 7,62мм 2. 4,4ц/га 3. 108км/час 4. 148,5; 221,3; 46° 5. 55°; 70,36; 45° 6. 42° 7. 64,7 8. 100; 1,96 9.»4°20' 10. 15,625 11. ~4,9м3; 0,65; 41° 12. ~12л 13. а)7,5м2, б) 14. 2.5, 37°, 53°, 90°, 3/5, 4/5, 4/3, 3/4 15. 16. 19/35, 1/5, 5/7 17. 18. Глава 8 1. (6,-4), (4,0), (-2,4), (7,-10), 2. (2,-17), (6,-16), (13/6, -23/6) 3. 0 Глава 9 1. (-1,-2); (-3,-4) 8. у=х+1, у=-х-1 у=х+1, у=-х+1 9. 31,25°; 32° Глава 10 7. а) 8. 5; (-3,0), (3,0) 9. 10. a) a=1/5; b=1/4; b) a=1, b=1/2 11. 12. 13. Глава 11 1. Квадрат со стороной 30м 2. Квадрат со стороной 200м Приложение
Таблица значений тригонометрических функций
Курсовое задание Геометрическая и арифметическая прогрессия циркулем и линейкой
Равносторонний треугольник, арки и треугольная решетка
Древние символы. Деление окружности на равные части
Решетки, пчелиные соты
Кресты, шестиугольная мозаика
Метод квадрата и его диагонали (пропорция 1:
Среднее геометрическое, золотое сечение, золотой прямоугольник
Золотые треугольники, золотой дракон
Спираль Архимеда
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.170.196 (0.012 с.) |

 – длина i-го звена ломаной (рис. 9). Из этого соотношения можно непосредственно вывести формулу для вычисления площади поверхности вращения:
– длина i-го звена ломаной (рис. 9). Из этого соотношения можно непосредственно вывести формулу для вычисления площади поверхности вращения:

 , и для шара R(j)=Rcosj. Следовательно:
, и для шара R(j)=Rcosj. Следовательно: .
.

 =2pRh+2pR2×0,18
=2pRh+2pR2×0,18
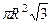
 ;
; 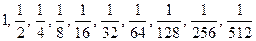 ;
; , 1, 2, 4, 8, 16; 16, 8, 4, 2, 1,
, 1, 2, 4, 8, 16; 16, 8, 4, 2, 1, 

 ; в)
; в)  ; г)~51,6м2
; г)~51,6м2
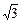


 ; б)
; б) 
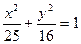 ; (-3,0), (3,0)
; (-3,0), (3,0)
 ,
, 
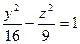 ,
, 












