
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трение скольжения. Законы трения скольжения. Реакция шероховатой поверхности. Угол трения.
Равновесие тел при наличии трения. Закон Кулона (закон Амонта – Кулона): максимальная сила сцепления пропорциональна нормальному давлению тела на плоскость
11) Центр тяжести твердого тела. Координаты центра тяжести тела. Способы определения положения центра тяжести: использование симметрии, разбиение на простые части, способ отрицательных масс. Центр тяжести твердого тела – точка, неизменно связанная с этим телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела при любом положении тела в пространстве. При этом поле тяжести считается однородным, т.е. силы тяжести частиц тела параллельны друг другу и сохраняют постоянную величину при любых поворотах тела. Координаты центра тяжести:
12) Способы задания движения точки. Скорость и ускорение точки при векторном способе задания ее движения. Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении. Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t). Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t). Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти). Векторный сп. положение точки определяется ее радиус-вектором ( модуль Переход от координатного способа к естественному: Скорость точки. Вектор ск-сти:
Ускорение точки.
13)Скорость и ускорение точки при координатном способе задания движения точки. Скорость и ускорение точки при естественном способе задания движения точки. Используем следующую теорему: проекция производной от вектора на ось, неподвижную в данной СО, равна производной от проекции дифференцируемого вектора на ту же ось. Тогда для проекций скорости имеем или Т.о., проекции скорости точки на координатные оси равны первым производным от проекций соответствующих координат точки по времени. Для проекций ускорения имеем т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени. Скорость и ускорение точки при естественном способе задания движения Здесь Определим скорость точки Проекция скорости точки на касательную к ее траектории
Очевидно, что Для ускорения точки имеем Т.к. т.е., ускорение равно сумме касательной и нормальной составляющих
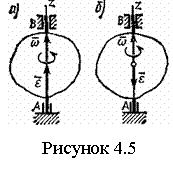
14)Вращательное движение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение вращающегося твердого тела. Скорости и ускорения точек вращающегося твердого тела. При вращении АТТ вокруг неподвижной оси, его точки, лежащие на оси, остаются неподвижными (АВ на рисунке 4.5). Через ось проведем две плоскости - неподвижную и подвижную, связанную с телом. Двугранный угол между ними называют углом поворота тела и считают положительным, когда он отсчитывается от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Закон вращения АТТ вокруг неподвижной оси – это = (t). (4.16) Угловая скорость характеризует изменение = d/dt или Угловую скорость тела можно изобразить в виде вектора Угловое ускорение характеризует изменение = d/dt = d2 /dt2 или Если во все время движения =cons, то вращение называют равномерным. Из формулы (4.17), интегрируя, найдем его закон При равномерном вращении, если Если угловое ускорение тела во все время движения остается постоянным (=const), то вращение называется равнопеременным, закон которого имеет вид Если и имеют одинаковые знаки, вращение - равноускоренное, если разные — равнозамедленное. Определим скорости и ускорения точек вращающегося тела (см. рисунок 4.6). При вращении точка М описывает окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр P лежит на оси. За время dt тело поворачивается на угол d, точка М совершает перемещение ds = h∙ d. Тогда Ускорения точки найдем как Ускорение а угол (см. рисунок 4.6) определяется зависимостью Для векторов Вращательное движение тела – такое движение твердого тела, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными. Эта прямая называется осью вращения тела. При этом движении все точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси вращения. Урав-ние (закон) вращательного движ.: j=f(t) – угол поворота тела в радианах. (1 рад= 180о/p=57,3о).
Угловая ск-сть: Вектор угловой скорости тела, совершающего вращение вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему навстречу вращение будет против час. стрелке. "n"– число оборотов в мин. [об/мин], 1об=2p рад, Частные случаи вращения тела: 1) Равномерное вращение: w=const, j=wt, w=j/t, 2) Равнопеременное вращение: w=w0+et; Скорости и ускорения точек вращающегося тела. Формулы Эйлера: wx,wy,wz – проекции вектора угловой скорости. Проекция вращательной (окружной) скорости: vx=wyz – wzy; vy=wzx – wxz; vz=wxy – wyx. Если ось вращения совпадает с осью z, то vx= – wy; vy=wx. Ускорение:
Основные понятия и аксиомы динамики. Дифференциальные уравнения движения материальной точки. Динамикой называют раздел механики, в котором рассматривается движение материальных тел под действием приложенных к ним сил с учетом инерции. Инерцией называется свойство материального тела сохранять состояние движения или покоя при отсутствии действующих на тело сил. Физическую величину, зависящую от количества вещества и являющуюся мерой инерции тела в поступательном движении, называется массой тела m. Основой динамики точки являются 4 аксиомы, изложенные ниже. 1-я аксиома (закон инерции): материальная точка (МТ), к которой не приложены силы, находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к ней силы не изменяют этого состояния. Движение МТ при отсутствии сил называют инерциальным. Систему отсчета (СО), в которой действует закон инерции, называют инерциальной СО. В большинстве задач СО, связанная с Землей, считается инерциальной. 2-я аксиома (основной закон динамики): ускорение МТ пропорционально приложенной к ней силе и направлено так же, как сила.Основное уравнение
3-я аксиома (закон о действии и противодействии): две МТ действуют друг на друга с равными по модулям силами, которые лежат на соединяющей эти точки прямой и направлены в противоположные стороны. 4-я аксиома (закон независимости действия сил): геометрическая сумма ускорений, которые сообщаются МТ отдельно каждой приложенной к ней силой, равна ускорению, которое МТ получит под действием на нее всех сил. Вместо (5.2) можно пользоваться уравнением (5.1), понимая под силой Под действием на тело силы тяжести у тела возникает одно и то же ускорение Масса тела не зависит от его местонахождения и от сил, приложенных к телу, а вес тела меняется с изменением ускорения силы тяжести в зависимости от географической широты места и расстояния от центра Земли. Для решения задач динамики точки будем пользоваться уравнениями в декартовых координатах:
Рассмотрим материальную точку, движущуюся под действием сил Решение первой задачи динамики (определение сил по заданному движению). Если ускорение движущейся точки задано, то действующая сила или реакция связи сразу находится по уравнению Решение основной задачи динамики при прямолинейном движении точки. Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться первым из уравнений Решение основной задачи динамики сводится к тому, чтобы из данных ур-й, зная силы, найти закон движения точки, т.е. х=f(t). Для этого надо проинтегрировать соответствующее дифф-е ур-е. Общее решение ур-я Необходимо определить значения постоянных С1 и С2. Для этого используются обычно так называемые начальные условия. По начальным условиям можно определить конкретные значения постоянных С1 и С2 и найти частное решение уравнения
16)Количество движения материальной точки. Импульс силы. Теорема об изменении количества движения материальной точки. Теорема об изменении момента количества движения материальной точки. При решении многих задач динамики вместо интегрирования ДУД оказывается более эффективным использование т.н. общих теорем динамики. Рассмотрим теорему об изменении количества движения точки.Количеством движения МТ называют величину mv, равную произведению массы точки на ее скорость. Вектор mv направлен по касательной к траектории точки. Элементарным импульсом силы называют величину (5.5) равную произведению силы на элементарный промежуток времени. Направлен импульс вдоль линии действия силы. Импульс S силы F за конечное время t1
Модуль и направление импульса можно вычислить по его проекциям Основной закон динамики можно представить в виде Это теорема об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Та же теорема в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за этот промежуток времени При решении задач обычно пользуются уравнениями в проекциях.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.79.70 (0.112 с.) |
 , fсц – коэффициент сцепления (зависит от материала, состояния поверхностей, определяется экспер-но). Направление силы сцепления противоположно направлению того движения, которое возникло бы при отсутствии сцепления. При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Ее направление противоположно скорости тела
, fсц – коэффициент сцепления (зависит от материала, состояния поверхностей, определяется экспер-но). Направление силы сцепления противоположно направлению того движения, которое возникло бы при отсутствии сцепления. При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Ее направление противоположно скорости тела  , f –коэффициент трения скольжения (определяется опытным путем). f<fсц. Реакция шероховатой (реальной) поверхности в отличии от идеально гладкой имеет две составляющие: нормальную реакцию и силу сцепления (или силу трения при движении). Угол jсц–угол сцепления (jтр – угол трения) tgjсц=fсц (tgjтр=f). Конус с вершиной в точке касания тел, образующая которого составляет угол сцепления (угол трения) с нормалью к поверхностям тела назыв. конусом сцепления (конус трения). Для того чтобы тело начало движение, необходимо (и достаточно), чтобы равнодействующая активных сил находилась вне конуса трения. Трение качения – сопротивление, возникающее при качении одного тела по поверхности другого. Причина его появления в деформации катка и плоскости в точке их соприкосновения и смещения нормальной реакции в сторону возможного движения. Мтр= fkN – момент трения качения, fk – коэффициент трения качения; имеет размерность длины.
, f –коэффициент трения скольжения (определяется опытным путем). f<fсц. Реакция шероховатой (реальной) поверхности в отличии от идеально гладкой имеет две составляющие: нормальную реакцию и силу сцепления (или силу трения при движении). Угол jсц–угол сцепления (jтр – угол трения) tgjсц=fсц (tgjтр=f). Конус с вершиной в точке касания тел, образующая которого составляет угол сцепления (угол трения) с нормалью к поверхностям тела назыв. конусом сцепления (конус трения). Для того чтобы тело начало движение, необходимо (и достаточно), чтобы равнодействующая активных сил находилась вне конуса трения. Трение качения – сопротивление, возникающее при качении одного тела по поверхности другого. Причина его появления в деформации катка и плоскости в точке их соприкосновения и смещения нормальной реакции в сторону возможного движения. Мтр= fkN – момент трения качения, fk – коэффициент трения качения; имеет размерность длины. ;
;  ;
;  , где Р=åрk, xk,yk,zk – координаты точек приложения сил тяжести рk. Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:
, где Р=åрk, xk,yk,zk – координаты точек приложения сил тяжести рk. Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:
 , DFk – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то
, DFk – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то  . Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a:
. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a:  ; кругового сектора:
; кругового сектора:  ; треугольник: в точке пересеч. медиан (1/3 медианы от основания).
; треугольник: в точке пересеч. медиан (1/3 медианы от основания). , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между координатным и векторным способами:
, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между координатным и векторным способами:  ,
, – орты – единичные вектора, сонаправленные с какой-либо осью)
– орты – единичные вектора, сонаправленные с какой-либо осью) , направляющие косинусы:
, направляющие косинусы:  и т.д.
и т.д. .
. – первая производная от радиус-вектора по времени (точка обозначает производную по времени);
– первая производная от радиус-вектора по времени (точка обозначает производную по времени);  . Проекции скорости:
. Проекции скорости:  ,
,  ,
,  . Модуль скорости:
. Модуль скорости: , направляющие косинусы:
, направляющие косинусы:  и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным. При естественном сп.:
и т.д. Если модуль скорости не изменяется с течением времени, то движение называется равномерным. При естественном сп.:  – модуль скорости, вектор скорости:
– модуль скорости, вектор скорости:  ,
,  – орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление
– орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если v>0, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление  , поперечное направление
, поперечное направление  , модуль скорости
, модуль скорости  ; x=rcosj, y=rsinj.
; x=rcosj, y=rsinj. , [м/сек2]. Проекции уск.-я:
, [м/сек2]. Проекции уск.-я: 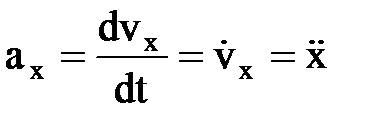 и т.д. Модуль уск.-я:
и т.д. Модуль уск.-я: 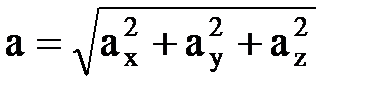 , направляющ. косинусы:
, направляющ. косинусы:  , и т.д.
, и т.д. При задании движения в полярных координатах: проекции ускорения на радиальное направление
При задании движения в полярных координатах: проекции ускорения на радиальное направление  , поперечное направление
, поперечное направление  , модуль ускорения
, модуль ускорения 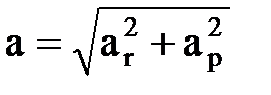 . При естественным сп. задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:
. При естественным сп. задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения: 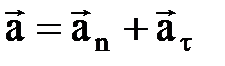 . Модуль нормального ускорения:
. Модуль нормального ускорения:  , r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения
, r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения  , направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движ-ии направление касат. уск. и скорости совпадают, при замедленном – противоположно.
, направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движ-ии направление касат. уск. и скорости совпадают, при замедленном – противоположно.  ^
^  , Þ
, Þ  . Вектор ускорения лежит в соприкасающейся плоскости Þ его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль – ^ к главной нормали и касательной).
. Вектор ускорения лежит в соприкасающейся плоскости Þ его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль – ^ к главной нормали и касательной). (4.6)
(4.6) . (4.7)
. (4.7) ,
,  ,
,  или
или  ,
, и
и  определяют по их проекциям на оси естественного трехгранника Мnb, имеющие начало в точке М и движущиеся вместе с нею (см. рисунок 4.5). Направления осей: М - по касательной к траектории в сторону положительного отсчета s; главная нормаль Мn -
определяют по их проекциям на оси естественного трехгранника Мnb, имеющие начало в точке М и движущиеся вместе с нею (см. рисунок 4.5). Направления осей: М - по касательной к траектории в сторону положительного отсчета s; главная нормаль Мn -  по нормали к траектории, лежащей в соприкасающейся плоскости, и направленной в сторону вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так, чтобы она образовывала с ними правую систему осей.
по нормали к траектории, лежащей в соприкасающейся плоскости, и направленной в сторону вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так, чтобы она образовывала с ними правую систему осей. .
.

 и модуль скорости
и модуль скорости  .
.
 (ρ – радиус кривизны траектории точки в рассматриваемом положении), то
(ρ – радиус кривизны траектории точки в рассматриваемом положении), то , (4.13)
, (4.13) Вектор
Вектор  лежит в соприкасающейся плоскости, т. е. в плоскости Mn. Проецируя обе части равенства (4.13) на оси М, Мn и Mb, получим
лежит в соприкасающейся плоскости, т. е. в плоскости Mn. Проецируя обе части равенства (4.13) на оси М, Мn и Mb, получим .
. зависимость
зависимость . (4.17)
. (4.17) с модулем, равным ||, и направленного вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки.
с модулем, равным ||, и направленного вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки.
 . (4.19)
. (4.19) , то
, то  . (4.20)
. (4.20) . (4.21)
. (4.21) . (4.21)
. (4.21)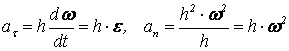 . (4.22)
. (4.22) направлено по касательной к траектории (в сторону движения при ускоренном вращении и в обратную сторону при замедленном), ускорение
направлено по касательной к траектории (в сторону движения при ускоренном вращении и в обратную сторону при замедленном), ускорение  всегда направлено по радиусу МP к оси. Полное ускорение точки равно
всегда направлено по радиусу МP к оси. Полное ускорение точки равно , (4.23)
, (4.23) . (4.24)
. (4.24) и
и  можно получить формулы
можно получить формулы , (4.25)
, (4.25) .
. , [рад/с] – определяет быстроту изменения угла поворота.
, [рад/с] – определяет быстроту изменения угла поворота. . Угловое ускорение тела:
. Угловое ускорение тела:  , [рад/с2]. Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении.
, [рад/с2]. Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении. , здесь начальный угол j0=0.
, здесь начальный угол j0=0. – скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.
– скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус–вектор этой точки. Модуль векторного произведения: v=w×r×sin(a)= w×(CM), (СМ) – расстояние от точки М до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка М, в сторону вращения.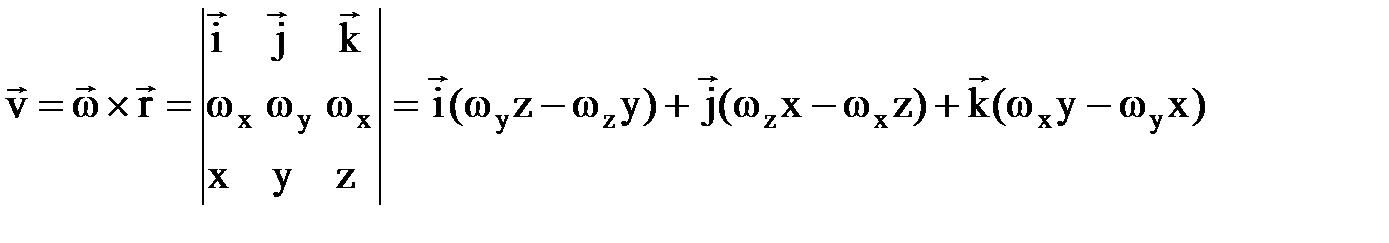 ,
,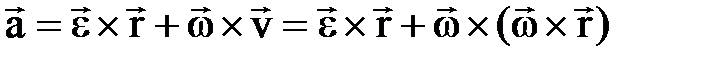 . Вращательное ускорение
. Вращательное ускорение  , модуль вращат. уск. авр=e×r×sina, направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное) ускорение
, модуль вращат. уск. авр=e×r×sina, направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное) ускорение  , ац=w2×R, направлено по радиусу к оси (центру) вращения. Модуль полного уск.:
, ац=w2×R, направлено по радиусу к оси (центру) вращения. Модуль полного уск.:  . Угол, между векторами полного и центростремит-ного ускорений:
. Угол, между векторами полного и центростремит-ного ускорений:  .
.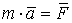 . (5.1)
. (5.1) (5.2)
(5.2) равнодействующую.
равнодействующую. , которое называют ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена только сила тяжести
, которое называют ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена только сила тяжести  , то по (5.1)
, то по (5.1) . (5.2)
. (5.2)
 по отношению к инерциальной системе отсчета Oxyz. Проектируя обе части равенства на оси х, у, z, получим:
по отношению к инерциальной системе отсчета Oxyz. Проектируя обе части равенства на оси х, у, z, получим:  или, обозначая вторые производные по времени двумя точками,
или, обозначая вторые производные по времени двумя точками,  . Это и будут искомые уравнения, т. е. дифференциальные уравнения движения точки в прямоугольных декартовых координатах.
. Это и будут искомые уравнения, т. е. дифференциальные уравнения движения точки в прямоугольных декартовых координатах.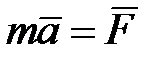 . При этом для вычисления реакции надо дополнительно знать активные силы. Когда ускорение непосредственно не задано, но известен закон движения точки, то для определения силы можно воспользоваться уравнениями
. При этом для вычисления реакции надо дополнительно знать активные силы. Когда ускорение непосредственно не задано, но известен закон движения точки, то для определения силы можно воспользоваться уравнениями  или
или  - дифф-ое ур-е прямолинейного движения точки. Иногда его удобнее заменить 2-мя ур-ми, содержащими первые производные:
- дифф-ое ур-е прямолинейного движения точки. Иногда его удобнее заменить 2-мя ур-ми, содержащими первые производные:  ,
, 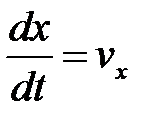 В случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t, ур-е
В случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t, ур-е 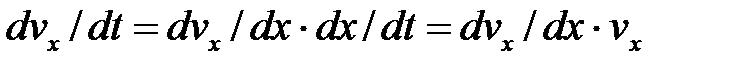 , то получим:
, то получим: 

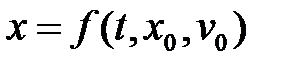

 . (5.6)
. (5.6) . (5.7)
. (5.7) . (5.8)
. (5.8) (5.9)
(5.9)


