
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связи и их реакции. Аксиома связей. Основные виды связейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия и аксиомы статики
Связи и их реакции. Аксиома связей. Основные виды связей
Теорема о параллельном переносе силы. Основная теорема статики о привидении системы сил к заданному центру (теорема Пуансо) Силу, приложенную к твердому телу, можно, не изменяя ее действия, перенести параллельно самой себе в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (см. рисунок 2.4). Три формы условий равновесия для произвольной плоской системы сил. Условия равновесия плоской системы параллельных сил. Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости, в которой лежат силы. В плоских системах нет необходимости использовать векторное представление момента. Теорема Вариньона – если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех сил относит. той же точки. Условия равновесия пл. сист. сил: векторное:
где А,В,С – точки, не лежащие на одной прямой, или Равновесие системы тел Связи, соединяющие части системы тел, называют внутренними. Если внешние связи заменить силами, то условий равновесия недостаточно для их определения. Методы решения таких задач: а) пользуясь свойствами внутренних связей, составляют дополнительные условия равновесия. Так, для системы на рисунке 3.1 а, четвертым уравнением будет равенство нулю суммы моментов относительно шарнира С всех сил, приложенных к какую-либо одной из ее половин;
б) мысленно расчленяют конструкцию на отдельные части, заменяя внутренние связи силами (см. рисунок 3.1 б). Для каждой половины имеем по три независимых условия равновесия, из которых находим шесть неизвестных. Основные понятия и аксиомы динамики. Дифференциальные уравнения движения материальной точки. Динамикой называют раздел механики, в котором рассматривается движение материальных тел под действием приложенных к ним сил с учетом инерции. Инерцией называется свойство материального тела сохранять состояние движения или покоя при отсутствии действующих на тело сил. Физическую величину, зависящую от количества вещества и являющуюся мерой инерции тела в поступательном движении, называется массой тела m. Основой динамики точки являются 4 аксиомы, изложенные ниже. 1-я аксиома (закон инерции): материальная точка (МТ), к которой не приложены силы, находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к ней силы не изменяют этого состояния. Движение МТ при отсутствии сил называют инерциальным. Систему отсчета (СО), в которой действует закон инерции, называют инерциальной СО. В большинстве задач СО, связанная с Землей, считается инерциальной. 2-я аксиома (основной закон динамики): ускорение МТ пропорционально приложенной к ней силе и направлено так же, как сила.Основное уравнение 3-я аксиома (закон о действии и противодействии): две МТ действуют друг на друга с равными по модулям силами, которые лежат на соединяющей эти точки прямой и направлены в противоположные стороны. 4-я аксиома (закон независимости действия сил): геометрическая сумма ускорений, которые сообщаются МТ отдельно каждой приложенной к ней силой, равна ускорению, которое МТ получит под действием на нее всех сил. Вместо (5.2) можно пользоваться уравнением (5.1), понимая под силой Под действием на тело силы тяжести у тела возникает одно и то же ускорение Масса тела не зависит от его местонахождения и от сил, приложенных к телу, а вес тела меняется с изменением ускорения силы тяжести в зависимости от географической широты места и расстояния от центра Земли. Для решения задач динамики точки будем пользоваться уравнениями в декартовых координатах:
Рассмотрим материальную точку, движущуюся под действием сил Решение первой задачи динамики (определение сил по заданному движению). Если ускорение движущейся точки задано, то действующая сила или реакция связи сразу находится по уравнению
Решение основной задачи динамики при прямолинейном движении точки. Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться первым из уравнений Решение основной задачи динамики сводится к тому, чтобы из данных ур-й, зная силы, найти закон движения точки, т.е. х=f(t). Для этого надо проинтегрировать соответствующее дифф-е ур-е. Общее решение ур-я Необходимо определить значения постоянных С1 и С2. Для этого используются обычно так называемые начальные условия. По начальным условиям можно определить конкретные значения постоянных С1 и С2 и найти частное решение уравнения
16)Количество движения материальной точки. Импульс силы. Теорема об изменении количества движения материальной точки. Теорема об изменении момента количества движения материальной точки. При решении многих задач динамики вместо интегрирования ДУД оказывается более эффективным использование т.н. общих теорем динамики. Рассмотрим теорему об изменении количества движения точки.Количеством движения МТ называют величину mv, равную произведению массы точки на ее скорость. Вектор mv направлен по касательной к траектории точки. Элементарным импульсом силы называют величину (5.5) равную произведению силы на элементарный промежуток времени. Направлен импульс вдоль линии действия силы. Импульс S силы F за конечное время t1
Модуль и направление импульса можно вычислить по его проекциям Основной закон динамики можно представить в виде Это теорема об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Та же теорема в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за этот промежуток времени При решении задач обычно пользуются уравнениями в проекциях. Основные понятия и аксиомы статики
Связи и их реакции. Аксиома связей. Основные виды связей
|
||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1083; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.123.194 (0.011 с.) |


 Аксиомы (законы) статики: 1) аксиома инерции: Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. 2) аксиома равновесия двух сил: Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны. 3) аксиома присоединения и исключения уравновешивающихся сил: Действие системы сил на абс. твердое тело не изменится, если к ней прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на абс.тв. тело не изменится, если перенести точку приложения силы вдоль ее линии действия. Т.е. сила, приложенная к абс.тв. телу– скользящий вектор. 4) аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
Аксиомы (законы) статики: 1) аксиома инерции: Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. 2) аксиома равновесия двух сил: Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны. 3) аксиома присоединения и исключения уравновешивающихся сил: Действие системы сил на абс. твердое тело не изменится, если к ней прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на абс.тв. тело не изменится, если перенести точку приложения силы вдоль ее линии действия. Т.е. сила, приложенная к абс.тв. телу– скользящий вектор. 4) аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах. 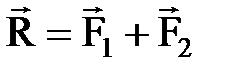 ;
; 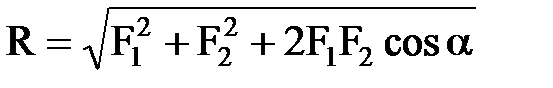 . 5) аксиома равенства действия и противодействия (3-й закон Ньютона): Всякому действию соответствует равное и противоположно направленное противодействие. 6) принцип отвердевания: Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании.
. 5) аксиома равенства действия и противодействия (3-й закон Ньютона): Всякому действию соответствует равное и противоположно направленное противодействие. 6) принцип отвердевания: Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании.
 Тело называется свободным, если его перемещения ничем не ограничены. Тело, перемещение которого ограничено другими телами, назыв. несвободным. Тела, ограничивающие перемещения данного тела, назыв. связями. Силы, с которыми связи действуют на данное тело, назыв. реакциями связей. Принцип освобождаемости: Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу. Основные типы связей: а) опора на идеально гладкую поверхность – реакция поверхности направлена по нормали к ней, т.е. перпендикулярно касательной – нормальная реакция; б) одна из соприкасающихся поверхностей является точкой (угол), реакция направлена по нормали к другой поверхности; в) нить – реакция направлена вдоль нити к точке подвеса; г) цилиндрический шарнир (шарнирно-неподвижная опора) – реакция может иметь любое направление в плоскости. При решении задач заменяется двумя взаимно перпендикулярными составляющими; д) цилиндрическая шарнирно-подвижная опора (шарнир на катках) – реакция направлена перпендикулярно опорной плоскости; е) сферический (шаровой) шарнир – реакция может иметь любое направление в пространстве. При решении задач заменяется тремя взаимно перпендикулярными составляющими; ж) невесомый стержень (обязательно невесомый) – реакция направлена вдоль стержня; з) "глухая" заделка (вмурованная балка) – возникает произвольно направленная реакция – сила и реактивный момент, также неизвестный по направлению. Реакция раскладывается на две составляющие.
Тело называется свободным, если его перемещения ничем не ограничены. Тело, перемещение которого ограничено другими телами, назыв. несвободным. Тела, ограничивающие перемещения данного тела, назыв. связями. Силы, с которыми связи действуют на данное тело, назыв. реакциями связей. Принцип освобождаемости: Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу. Основные типы связей: а) опора на идеально гладкую поверхность – реакция поверхности направлена по нормали к ней, т.е. перпендикулярно касательной – нормальная реакция; б) одна из соприкасающихся поверхностей является точкой (угол), реакция направлена по нормали к другой поверхности; в) нить – реакция направлена вдоль нити к точке подвеса; г) цилиндрический шарнир (шарнирно-неподвижная опора) – реакция может иметь любое направление в плоскости. При решении задач заменяется двумя взаимно перпендикулярными составляющими; д) цилиндрическая шарнирно-подвижная опора (шарнир на катках) – реакция направлена перпендикулярно опорной плоскости; е) сферический (шаровой) шарнир – реакция может иметь любое направление в пространстве. При решении задач заменяется тремя взаимно перпендикулярными составляющими; ж) невесомый стержень (обязательно невесомый) – реакция направлена вдоль стержня; з) "глухая" заделка (вмурованная балка) – возникает произвольно направленная реакция – сила и реактивный момент, также неизвестный по направлению. Реакция раскладывается на две составляющие.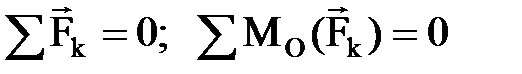 . аналитич:
. аналитич: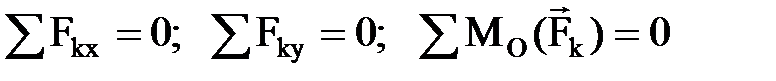 , или
, или 
 , ось "х" не перпендикулярна отрезку АВ.
, ось "х" не перпендикулярна отрезку АВ.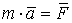 . (5.1)
. (5.1) (5.2)
(5.2) равнодействующую.
равнодействующую. , которое называют ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена только сила тяжести
, которое называют ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена только сила тяжести  , то по (5.1)
, то по (5.1) . (5.2)
. (5.2)
 по отношению к инерциальной системе отсчета Oxyz. Проектируя обе части равенства на оси х, у, z, получим:
по отношению к инерциальной системе отсчета Oxyz. Проектируя обе части равенства на оси х, у, z, получим:  или, обозначая вторые производные по времени двумя точками,
или, обозначая вторые производные по времени двумя точками,  . Это и будут искомые уравнения, т. е. дифференциальные уравнения движения точки в прямоугольных декартовых координатах.
. Это и будут искомые уравнения, т. е. дифференциальные уравнения движения точки в прямоугольных декартовых координатах.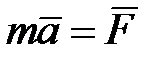 . При этом для вычисления реакции надо дополнительно знать активные силы. Когда ускорение непосредственно не задано, но известен закон движения точки, то для определения силы можно воспользоваться уравнениями
. При этом для вычисления реакции надо дополнительно знать активные силы. Когда ускорение непосредственно не задано, но известен закон движения точки, то для определения силы можно воспользоваться уравнениями  или
или  - дифф-ое ур-е прямолинейного движения точки. Иногда его удобнее заменить 2-мя ур-ми, содержащими первые производные:
- дифф-ое ур-е прямолинейного движения точки. Иногда его удобнее заменить 2-мя ур-ми, содержащими первые производные:  ,
, 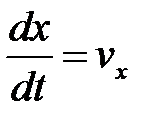 В случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t, ур-е
В случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t, ур-е 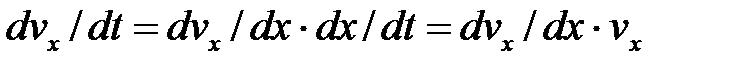 , то получим:
, то получим: 

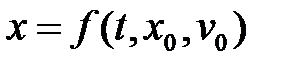

 . (5.6)
. (5.6) . (5.7)
. (5.7) . (5.8)
. (5.8) (5.9)
(5.9)


