
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении момента количества движения точкиСодержание книги
Поиск на нашем сайте
Моментом количества движения точки относительно некоторого центра О называется векторная величина где При этом вектор Момент количества движения точки относительно какой-нибудь оси Оz, проходящей через центр О, равен проекции вектора Теорема: производная по времени от момента количества движения точки, взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра Теорема моментов относительно оси Из уравнения (5.20) следует, что если
17)Работа и мощность силы. Теорема об изменении кинетической энергии точки. Элементарной работой силы dW = F ∙ds (5.14) где F — проекция силы ds — модуль элементарного перемещения точки М. Т.к. ds = |d dW= Т.е., элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения. Работа силы на конечном перемещении M0M1 (см. рисунок 5.1) определяется как Мощностью называют величину, равную работе, совершаемой силой в единицу времени. Если работа совершается равномерно, то мощность P = W/t1 (здесь t1 - время, течение которого произведена работа W). В общем случае т.е., мощность равна произведению касательной составляющей силы на скорость. Кинетической энергией (КЭ) точки называют скалярную величину
18)Понятие о механической системе. Масса и центр масс системы. Моменты инерции системы и тела. Теорема Гюйгенса-Штейнера. Осевой момент инерции механической системы. Моментом инерции механической системы относительно неподвижной оси a ("осевой момент инерции") называется физическая величина Ja равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
Теорема Штейнера Если I 0 — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии d от неё, равен I = I 0 + md 2, где m — полная масса тела. Например, момент инерции стержня относительно оси, проходящей через его конец, равна:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.005 с.) |

 , определяемая равенством
, определяемая равенством (5.10)
(5.10) — радиус-вектор движущейся точки, проведенный из центра О.
— радиус-вектор движущейся точки, проведенный из центра О. направлен перпендикулярно плоскости, проходящей через
направлен перпендикулярно плоскости, проходящей через 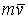 и центр О, a
и центр О, a  .
. где — угол между вектором
где — угол между вектором  и осью Оz.
и осью Оz. . (5.12)
. (5.12) . (5.13)
. (5.13) , то
, то  .
. , приложенной в точке М (см. рисунок 5.1), называют скалярную величину
, приложенной в точке М (см. рисунок 5.1), называют скалярную величину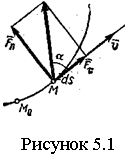 сторону перемещения точки;
сторону перемещения точки; . (5.15)
. (5.15) , (5.24)
, (5.24) . (5.25)
. (5.25)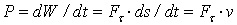 (5.16)
(5.16) . Теорема: изменение КЭ точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
. Теорема: изменение КЭ точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
 , Осевой момент инерции тела. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
, Осевой момент инерции тела. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.  , где: dm = ρ dV — масса малого элемента объёма тела dV, ρ — плотность, r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
, где: dm = ρ dV — масса малого элемента объёма тела dV, ρ — плотность, r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то  Момент инерции данного тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера) момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Момент инерции данного тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера) момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: 





 Центральный момент инерции. Центральный момент инерции JO (или момент инерции относительно точки O) - это величина
Центральный момент инерции. Центральный момент инерции JO (или момент инерции относительно точки O) - это величина  . Главные оси инерции. Главные моменты инерции. tg2α0 =2 Dxy / (Iy – Ix). Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой — минимален, Такие оси называют главными. Моменты инерции относительно главных осей называются главными моментами инерции.
. Главные оси инерции. Главные моменты инерции. tg2α0 =2 Dxy / (Iy – Ix). Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой — минимален, Такие оси называют главными. Моменты инерции относительно главных осей называются главными моментами инерции.


