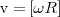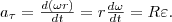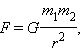Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Две основные задачи статики.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Аксиомы статики
Статикой называется раздел теоретической механики в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил. Под равновесием понимают состояние покоя тела по отношению к инерциальной системе отсчета, связанной обычно с неподвижным телом. В качестве модели реального материального тела, в статике рассматривается абсолютно твердое тело - тело расстояние между любыми двумя точками которого всегда остается постоянным. Совокупность сил, действующих на твердое тело, называется системой сил. В основе статики лежат аксиомы - экспериментально установленные законы, справедливость которых проверена практической деятельностью человека.
F1 = -F2. Система сил F1 и F2 называется уравновешивающейся, или эквивалентной нулю: F1 + F2 = 0. (Здесь и далее векторные величины выделены жирным шрифтом). Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил. Следствие. Не нарушая состояния твердого тела, силу можно переносить по линии ее действия в любую точку тела, т. е. сила - вектор скользящий.
R=F1 + F2. Сила R, которая эквивалентна данной системе сил F1 и F2 называется равнодействующей. Ее модуль вычисляется по формуле
где - угол между силами F1 и F2.
FA= -FB. Cилы FA и FB не образуют уравновешенную систему сил, так как они приложены к разным телам. Аксиома 5.Равновесие деформируемого тела не нарушится, если тело считать отвердевшим (абсолютно твердым). Следует помнить, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но не достаточными для соответствующего деформируемого тела. Две основные задачи статики. 1. Задача о приведении системы сил: заключается в замене данной стстемы сил другой, наиболее простой, ей эквивалентной. 2. Задача о равновесии состоит в определении условий, при которых система сил приложенная к телу будетуравновешенной системой.
2.Закон параллелограмма сил.закон равенства действия противодействию.
Закон параллелограмма сил: две силы F 1 и F 2, приложенные к телу в одной точке, имеют равнодействующую силу R, приложенную в той же точке и являющуюся диагональю параллелограмма, построенного на этих силах, как на сторонах. Вектор R называют геометрической суммой векторов F 1 и F 2: R = F 1+ F 2. R=(F12+F22+2F1F2cos где Принцип отвердения: равновесие деформируемого твердого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твердым. 2. закон деиствияпротиводеиствию- ньютон
Принцип отвердевания тела. Отвердевания принцип, одно из исходных положений статики, согласно которому состояние равновесия изменяемой механической системы не нарушается при отвердевании системы. К изменяемым относятся системы материальных точек, связанных между собой силами взаимодействия, системы твёрдых тел, соединённых шарнирами, стержнями или нитями, и системы частиц деформируемой среды — деформируемого твёрдого тела, жидкости или газа. О. п. устанавливает, что если изменяемая система находится в равновесии, то это состояние равновесия не может быть нарушено присоединением дополнительных связей между точками и телами системы. На основании О. п. в число необходимых (но недостаточных) условий равновесия изменяемой или деформируемой системы, находящейся под действием данных сил, входят все условия равновесия абсолютно твёрдого тела, находящегося под действием тех же сил. Следовательно, при составлении необходимых условий равновесия любую изменяемую систему можно рассматривать как абсолютно твёрдое тело. Этим широко пользуются в инженерной практике при изучении равновесия изменяемых систем.
Сложение системы сил сложе́ние сил нахождение геометрической суммы (так называемого главного вектора) данной системы сил путём последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая. * * * СЛОЖЕНИЕ СИЛ СЛОЖЕ́НИЕ СИЛ, нахождение геометрической суммы (т. н. главного вектора) данной системы сил путем последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая.
5. Аналитический способ сложения сил
где Fkx, Fky - проекции k-ой силы Fk на оси Ох и Оу соответственно. Тогда на плоскости Оху вектор R равные геометрической сумме слагаемых сил F1, F2,..., Fn определяется по формулам:
Пара сил. Момент пары сил
F = - F'; F=F'. Расстояние d между линиями действия сил пары называется плечом пары; плоскость Пара сил не имеет равнодействующей. Она стремится сообщить телу некоторое вращение. Вращательный эффект пары характеризуется векторной величиной, называемой моментом пары. Момент пары сил относительно точки O MO (F, F') = MO (F) + MO (F') не зависит от выбора точки O и равен моменту одной из сил пары относительно точки приложения другой силы M (F, F') = MA (F') = MB (F). Момент пары сил M перпендикулярен плоскости действия пары, направлен по правилу правого винта и равен по модулю произведению модуля любой из сил на плечо пары: M = F · d. Векторный момент пары сил может быть приложен в любой точке пространства, т.е. является свободным вектором. Две пары сил, имеющие одинаковые векторные моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие. Эквивалентность пар: действие пары сил на твердое тело не изменится, если · переместить пару в другое положение в плоскости ее действия; · плоскость ее действия переместить параллельно самой себе; · любым образом изменить модули сил и плечо пары, сохранив неизменным их произведение, т.е. момент пары M=F · d. Сложение пар сил: система n пар сил с моментами M 1, M 2,..., M n эквивалентна одной паре с моментом M, равным векторной сумме моментов этих пар: M = Условие равновесия системы пар, приложенных к твердому телу: M = Законы трения скольжения. Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
Трение качения. Трение качения называется сопротивление возникающее при качении одного тела по поверхности другого.Это сопративлление обясняет деформацию тел в зоне их контакта. Значение деформации зависит от материала тел и действущих на них сил.ш Центр тяжести твердого тела На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую Для тел, размеры которых малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполнены эти два условия, называют однородным полем тяжести. Равнодействующая G сил тяжести, действующих на частицы данного тела, называется весом тела. По модулю вес тела равен произведению его массы m на ускорение свободного падения g Центром тяжести тела называется неизменно связанная с этим телом точка С, через которую проходят линии действия веса тела при любом положении тела в пространстве (см.рис.). Такая точка всегда существует и является примером так называемого центра параллельных сил. Центр тяжести тела является геометрической точкой, которая может распологаться вне пределов данного тела (например, для кольца).
Кинематика.
Пусть точка Р движется в пространстве относительно некоторой системы отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор r, проведенный из начала координат в точку Р. При движении точки Р вектор r будет изменяться с течением времени t, вообще говоря, и по модулю, и по направлению. Следовательно, r является переменным вектором (вектором-функцией), зависящим от аргумента t: r = r (t). Эта векторная функция определяет закон движения точки в векторной форме, так как она позволяет в любой момент времени построить вектор r и найти положение движущейся точки. Геометрическое место концов векторов r (t), называемое также годографом вектора r, определяет траекторию движущейся точки. Как известно, вектор может быть задан аналитически либо его модулем и углами с осями координат, либо его проекциями на эти оси. При прямолинейном движении вектор a направлен вдоль прямой, по которой движется точка. Если траекторией является пространственная кривая, то вектор a направлен в сторону вогнутости траектории и лежит в соприкасающейся плоскости. Так называют плоскость, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении d r = v dt движущейся точки (подробнее это понятие изложено при задании движения точки естественным способом). Для пространственной кривой в каждой ее точке будет, вообще говоря, своя соприкасающаяся плоскость. Для плоской кривой соприкасающаяся плоскость совпадает с плоскостью этой кривой и является общей для всех ее точек. В качестве единицы измерения ускорения применяется обычно м/с2.
Координатный способ задания движения точки Рассмотрим движение в пространстве точки Р по отношению к декартовой прямоугольной системе координат Oxyz. Проекции rx, ry, rz ее радиуса-вектора r равны декартовым координатам точки: rx= x, ry= y, rz= z (см. рис.). Следовательно, зависимость r (t) будет известна, если будут заданы координаты x, y, z как функции времени. Чтобы знать закон движения точки, то есть ее положение в пространстве в любой момент времени, надо задать зависимость координат точки по времени: x = x(t); y = y(t); z = z(t). Эти зависимости представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. Движение точки можно задавать с использованием и других систем координат, например, вполярных координатах. Если движение точки происходит все время в одной и той же плоскости, то, приняв эту плоскость за координатную плоскость Oxy, получим в этом случае два уравнения движения: x = x(t); y = y(t). При прямолинейном движении точки, если вдоль ее траектории направить ось Ox, движение будет определяться одним уравнением (законом прямолинейного движения точки): x = x(t).
Естественный способ задания движения точки
Пусть кривая АВ является траекторией точки Р при ее движении относительно системы отсчета Oxyz. Выберем на этой траектории какую-нибудь фиксированную точку O*, которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Тогда положение точки Р на траектории будет однозначно определяться криволинейной (дуговой) координатой s, которая равна расстоянию от точки O* до точки Р, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка Р перемещается по траектории и, следовательно, координата s будет с течением времени изменяться. Чтобы знать положение точки Р на траектории в любой момент времени, надо знать зависимость s = s(t). Это уравнение и выражает закон движения точки вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо знать:
Заметим, что координата s определяет положение движущейся точки, а не пройденный ею путь. Например, пусть точка Р начинает движение из начала отсчета O* в положительном направлении, доходит до некоторого положения, останавливается и затем перемещается в обратном направлении. Тогда до остановки точки координата s и пройденный ею путь будут совпадать, а после остановки будут отличаться, так как координата s будет уменьшаться, а пройденный путь по-прежнему будет увеличиваться.
18. Определение скорости и ускорения точки при координатном способе задания движения
Связь векторного способа задания движения и координатного дается соотношением
Из определения скорости
Проекции скорости на оси координат равны производным соответствующих координат по времени:
Модуль и направление скорости определяются выражениями
Из определения ускорения
Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени
Модуль и направление ускорения определяются выражениями
Фывфывфывфвфывфыв Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:
Вектор Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению. Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:
Вектор Из рис. 1.1.5 видно, что модуль полного ускорения равен
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение
Рис.1
т.е v = ωR
В векторном виде формулу для линейной скорости можно написать как векторное произведение:
При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.
Рис.2
Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда Т = 2π/ω.
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: n= 1/T = ω/(2π),
ω = 2πn.
Рис.3
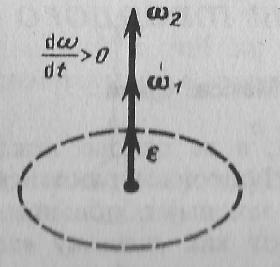
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).
Рис.4
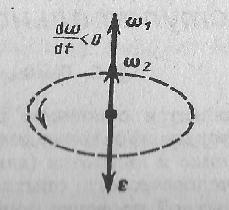
Тангенциальная составляющая ускорения aτ=dv/dt, v = ωR и
Нормальная составляющая ускорения
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аτ, нормальное ускорение аn) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами: s = Rφ, v = Rω, аτ = R?, an = ω2R.
В случае равнопеременного движения точки по окружности (ω=const) ω = ω0 ±?t, φ = ω0t ±?t2/2,
где ω0 — начальная угловая скорость.
Законы и задачи динамики
Основные виды сил
Закон всемирного тяготения. Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния r между ними:
где G = 6,67·10–11 м3/кг·с 2 (СИ) – гравитационная постоянная Сила, с которой тело действует на неподвижную горизонтальную опору или подвес, называется весом тела P=mg. По третьему закону Ньютона, с той же по модулю силой опора или подвес действуют на тело; эта сила называется реакцией опоры N. Понятие веса может быть распространено и на случай, когда опора или подвес движутся с ускорением относительно инерциальных систем. Если опора или подвес двигается с некоторым ускорением, то сила давления со стороны тела (то есть вес тела) изменяется. В частности, если опора движется с ускорением g направленным против силы тяжести, то вес тела обращается в нуль. Такое состояние называют невесомостью. Состояние невесомости испытывает космонавт в космическом корабле. Изменение формы или размеров тела называется деформацией. Деформации бывают упругими и пластичными
F=-kx
Силы, действующие между поверхностями соприкасающихся твердых тел, называются силами сухого трения. Они всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, скольжения и качения. F=µN
24. Дифференциальные уравнения движения материальной точки в декартовых координатах Рассматривается свободная материальная точка, движущаяся под действием сил 12F1,F2…Fn ´>по отношению к инерциальной системе отсчета (рис.2). При проецировании обеих частей равенства на оси 12x, y, z´>получаются дифференциальные уравнения движения материальной точки в проекциях на оси прямоугольной декартовой системы координат: Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у,z и проекции ее скорости на оси декартовой системы координат При этом в правую часть каждого из уравнений могут входить все эти переменные, то есть t, х, у,z, 12 x, y, z´> одновременно. Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, то есть положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при При известных значениях действующих сил, после интегрирования уравнений находятся координаты х,y,z движущейся точки, как функции времени t, т.е. находится закон движения точки [1,2 и др.]. Наше исследование заключалось в том, чтобы рассмотреть по каким законам материальная точка меняет своё положение в криволинейных системах координат, которые редко затрагиваются в стандартных учебных пособиях по теоретической механике. Также мы рассмотрели дифференциальные уравнения движения материальной точки в естественных координатах, обратившись к теории дифференциальной геометрии кривых. 25. Дифференциальные уравнения в проекциях на оси естественного трёхгранника В середине девятнадцатого века французский математик Ж. Френе написал знаменитые уравнения, помогающие описать движение ориентируемой точки вдоль произвольной кривой 12r(s)´>, где s - это длина дуги. Под ориентируемой точкой понимается трехгранник Френе (репер), образованный тремя единичными ортогональными векторами. Под репером Френе понимают тройку векторов сопоставленную каждой точке произвольной кривой где
к кривой в данной точке (рис. 3). Если s - натуральный параметр вдоль кривой, то векторы связаны соотношениями: называемыми формулами Френе. Величины: называют, соответственно, кривизной и кручением кривой в данной точке. Френе впервые показал, что произвольная кривая в общем случае определяется двумя параметрами: кривизной и кручением. Уравнения вида всюду положительна называются натуральными уравнениями произвольной кривой и полностью её определяют. Скорость и ускорение в осях естественного трёхгранника. Трёхгранник Френе играет важную роль при описании движения точки в «сопутствующих осях». Пусть материальная точка движется по произвольной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору 12v=vП„´>. Дифференцируя по времени находим выражение для ускорения: Компоненту при векторе 12П„´> называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе называют нормальным ускорением. Она характеризует изменение скорости по направлению [3]. Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трёхгранника. Составим основное уравнение динамики и спроецируем его на естественные оси: Так как, то получим дифференциальные уравнения движения: Также мы рассмотрели дифференциальные уравнения движения материальной точки в криволинейных системах координат, сначала обратимся к полярной системе координат.
Аксиомы статики
Статикой называется раздел теоретической механики в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил. Под равновесием понимают состояние покоя тела по отношению к инерциальной системе отсчета, связанной обычно с неподвижным телом. В качестве модели реального материального тела, в статике рассматривается абсолютно твердое тело - тело расстояние между любыми двумя точками которого всегда остается постоянным. Совокупность сил, действующих на твердое тело, называется системой сил. В основе статики лежат аксиомы - экспериментально установленные законы, справедливость которых проверена практической деятельностью человека.
F1 = -F2. Система сил F1 и F2 называется уравновешивающейся, или эквивалентной нулю: F1 + F2 = 0. (Здесь и далее векторные величины выделены жирным шрифтом). Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил. Следствие. Не нарушая состояния твердого тела, силу можно переносить по линии ее действия в любую точку тела, т. е. сила - вектор скользящий.
R=F1 + F2. Сила R, которая эквивалентна данной системе сил F1 и F2 называется равнодействующей. Ее модуль вычисляется по формуле
где - угол между силами F1 и F2.
FA= -FB. Cилы FA и FB не образуют уравновешенную систему сил, так как они приложены к разным телам. Аксиома 5.Равновесие деформируемого тела не нарушится, если тело считать отвердевшим (абсолютно твердым). Следует помнить, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но не достаточными для соответствующего деформируемого тела. Две основные задачи статики. 1. Задача о приведении системы сил: заключается в замене данной стстемы сил другой, наиболее простой, ей эквивалентной. 2. Задача о равновесии состоит в определении условий, при которых система сил приложенная к телу будетуравновешенной системой.
2.Закон параллелограмма сил.закон равенства действия противодействию.
Закон параллелограмма сил: две силы F 1 и F 2, приложенные к телу в одной точке, имеют равнодействующую силу R, приложенную в той же точке и являющуюся диагональю параллелограмма, построенного на этих силах, как на сторонах. Вектор R называют геометрической суммой векторов F 1 и F 2: R = F 1+ F 2. R=(F12+F22+2F1F2cos где Принцип отвердения: равновесие деформируемого твердого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твердым. 2. закон деиствияпротиводеиствию- ньютон
Принцип отвердевания тела. Отвердевания принцип, одно из исходных положений статики, согласно которому состояние равновесия изменяемой механической системы не нарушается при отвердевании системы. К изменяемым относятся системы материальных точек, связанных между собой силами взаимодействия, системы твёрдых тел, соединённых шарнирами, стержнями или нитями, и системы частиц деформируемой среды — деформируемого твёрдого тела, жидкости или газа. О. п. устанавливает, что если изменяемая система находится в равновесии, то это состояние равновесия не может быть нарушено присоединением дополнительных связей между точками и телами системы. На основании О. п. в число необходимых (но недостаточных) условий равновесия изменяемой или деформируемой системы, находящейся под действием данных сил, входят все условия равновесия абсолютно твёрдого тела, находящегося под действием тех же сил. Следовательно, при составлении необходимых условий равновесия любую изменяемую систему можно рассматривать как абсолютно твёрдое тело. Этим широко пользуются в инженерной практике при изучении равновесия изменяемых систем.
Сложение системы сил сложе́ние сил нахождение геометрической суммы (так называемого главного вектора) данной системы сил путём последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая. * * * СЛОЖЕНИЕ СИЛ СЛОЖЕ́НИЕ СИЛ, нахождение геометрической суммы (т. н. главного вектора) данной системы сил путем последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая.
5. Аналитический способ сложения сил
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 4102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.019 с.) |

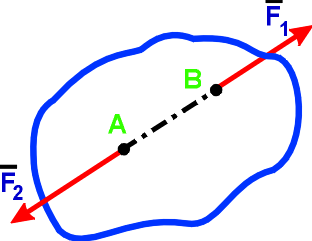 Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находится в равновесии только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны:
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находится в равновесии только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны:
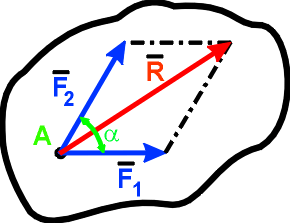 Аксиома 3. Две силы, приложенные к телу в одной точке, можно заменить одной, приложенной в той же точке, которая является диагональю параллелограмма, построенного на этих силах как на сторонах:
Аксиома 3. Две силы, приложенные к телу в одной точке, можно заменить одной, приложенной в той же точке, которая является диагональю параллелограмма, построенного на этих силах как на сторонах: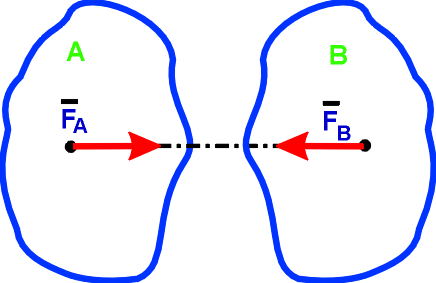 Аксиома 4. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны:
Аксиома 4. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны: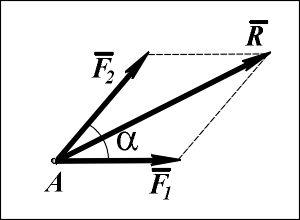
 )
) 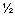 ;
; - угол между силами F 1 и F 2.
- угол между силами F 1 и F 2.
 Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Спроецируем равенство R = Fk на оси прямоугольной системы координат Оху, получим
Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Спроецируем равенство R = Fk на оси прямоугольной системы координат Оху, получим Fkx, Ry =
Fkx, Ry = 
 Парой сил называется приложенная к твердому телу система двух сил (F, F'), равных по модулю, параллельных и направленных в противоположные стороны:
Парой сил называется приложенная к твердому телу система двух сил (F, F'), равных по модулю, параллельных и направленных в противоположные стороны: , в которой действуют силы пары, называется плоскостью действия пары. Совокупность нескольких пар, действующих на тело, называется системой пар.
, в которой действуют силы пары, называется плоскостью действия пары. Совокупность нескольких пар, действующих на тело, называется системой пар. M k.
M k.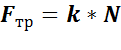 , где
, где называют силой тяжести. Эти силы образуют поле силы тяжести.
называют силой тяжести. Эти силы образуют поле силы тяжести. 9.81 м / c2: G = m · g.
9.81 м / c2: G = m · g.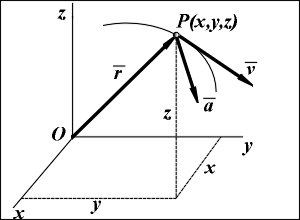 17.Векторный способ задания движения точки
17.Векторный способ задания движения точки Естественным способом задания движения точки удобно пользоваться в тех случаях, когда траектория движущейся точки заранее известна.
Естественным способом задания движения точки удобно пользоваться в тех случаях, когда траектория движущейся точки заранее известна.






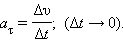
 направлен по касательной к траектории.
направлен по касательной к траектории.

 всегда направлен к центру окружности (см. §1.6).
всегда направлен к центру окружности (см. §1.6).
 , скорость
, скорость  и ускорение
и ускорение 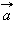 . Путь l является скалярной величиной. Перемещение
. Путь l является скалярной величиной. Перемещение